
- •Министерство образования
- •Введение
- •1. Кинематика точки
- •1.1. Способы задания движения точки
- •1.2. Скорость точки
- •В случае векторного способа задания движения вектор скорости точки равен первой производной по времени от ее радиус-вектора
- •1.4. Частные случаи движения точки
- •Вопросы для самоконтроля
- •2. Кинематика твердого тела
- •2.1. Понятие о степенях свободы твердого тела
- •2.2. Поступательное движение твердого тела
- •2.3. Вращение твердого тела вокруг неподвижной оси
- •2.4. Преобразования простейших движений твердого тела
- •Вопросы для самоконтроля
- •3. Плоскопараллельное движение твердого тела
- •3.1. Уравнения плоскопараллельного движения. Разложение движения на поступательное и вращательное
- •3.2. Определение скоростей и ускорений точек тела
- •3.3. Мгновенный центр скоростей
- •Вопросы для самоконтроля
- •4.Задания к контрольным работам
- •4.1. Определение скорости и ускорения точки по заданным уравнениям ее движения Задание к1
- •4.2. Преобразование простейших движений твердого тела Задание к2
- •4.3. Определение скоростей точек тела при плоскопараллельном движении Задание к3
- •1,49 М.
- •1,35 Рад/с.
- •0,81 М/с;
- •0,48 Рад/с.
- •1,59 М.
- •1.25 Рад/с.
- •Список рекомендуемой ЛитературЫ
- •Содержание
- •Теоретична механіка. Кінематика
- •61002, Харків, вул. Фрунзе, 21
4.3. Определение скоростей точек тела при плоскопараллельном движении Задание к3
4.3.1. Примеры решения контрольного задания К3
Пример 1. Катушка катится без скольжения в вертикальной плоскости по наклонному пути (рис.4.5).
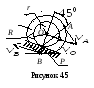 Найти
угловую скорость катушки, скорости
точекО иВ, если в рассматриваемый
момент времени
Найти
угловую скорость катушки, скорости
точекО иВ, если в рассматриваемый
момент времени![]() =
2 м/с,
=
2 м/с,
r= 0.6 м,R= 1 м.
Решение
Катушка совершает
плоскопараллельное движение. Так как
качение происходит без скольжения, то
скорость точкиРкасания катушкис неподвижной
поверхностью ![]() ,
следовательно эта точка является
мгновенным центром скоростей
(МЦС).Вектор скорости
точки А
,
следовательно эта точка является
мгновенным центром скоростей
(МЦС).Вектор скорости
точки А
![]() перпендикулярен АР
и направлен в сторону
качения катушки, а численное значение
скорости пропорционально расстоянию
от точки А до
МЦС:
перпендикулярен АР
и направлен в сторону
качения катушки, а численное значение
скорости пропорционально расстоянию
от точки А до
МЦС:
![]() ,
,
где ![]()
1,49 М.
Определим угловую скорость катушки
1,35 Рад/с.
Так как скорости точек ОиВкатушки также пропорциональны их расстояниям до точкиР, то
0,81 М/с;
![]() =
0,54 м/с.
=
0,54 м/с.
Направление вращения катушки, а,
следовательно, и направления скоростей
точек ВиО, определяются
направлением вектора скорости![]() по отношению кМЦС.
по отношению кМЦС.
Пример 2.
Стержень АВимеет
на концах ползуны, один из которыхАскользит по прямолинейной направляющей
со скоростью![]() =
= 1 м/с.
=
= 1 м/с.
Найти в положении, указанном на рис. 4.6, угловую скорость стержня, скорости точек В иС, еслиАВ = 1,2 м,АС=ВС.

Решение
Стержень АВсовершает плоскопараллельное движение. Так как скорости точекАиВнаправлены параллельно соответствующим направляющим, вдоль которых скользят ползуны, то, восстанавливая из точекАиВ перпендикуляры к скоростям этих точек, определим положение мгновенного центра скоростей стержняАВ – точкаР. ТреугольникАВРявляется равнобедренным, следовательно,АВ=ВР= 1,2м.
Скорость точки А пропорциональна
расстоянию от этой точки до точкиР:![]() ,
где
,
где![]() 2,08
м.
2,08
м.
Вычислим угловую скорость стержня АВ
0,48 Рад/с.
Скорость точки В определим по формуле
![]() = 0,48·1,2 = 0,58 м/с.
= 0,48·1,2 = 0,58 м/с.
Для определения скорости точки С найдем расстояниеРСс помощью теоремы косинусов
1,59 М.
Тогда скорость точки С
![]() = 0,76 м/с.
= 0,76 м/с.
Пример 3.
КривошипОАдлинойr= 1
м вращается с угловой скоростью![]() =
2 рад/с, приводя в движение шатунАВдлинойl= 4 м, как показано на рис.
4.7.
=
2 рад/с, приводя в движение шатунАВдлинойl= 4 м, как показано на рис.
4.7.
Определить скорость ползуна В,
угловую скорость шатуна![]() в двух положениях механизма, когда угол
поворота кривошипаj= 0 иj= 900.
в двух положениях механизма, когда угол
поворота кривошипаj= 0 иj= 900.

Решение
Шатун АВсовершает плоскопараллельное
движение. При этом![]() ,
так как точкаАпринадлежит кривошипуОА, совершающему вращательное
движение. Скорость ползунаВпараллельна направляющим. Численное
значение скорости точкиА
,
так как точкаАпринадлежит кривошипуОА, совершающему вращательное
движение. Скорость ползунаВпараллельна направляющим. Численное
значение скорости точкиА
![]() =2·1=2
м/с.
=2·1=2
м/с.
Найдем положение мгновенного центра
скоростей, восстанавливая перпендикуляры
к скоростям точек АиВ из этих
точек. При углеj= 0
(см. рис. 4.7,а) перпендикуляр к скорости![]() и перпендикуляр к направлению
и перпендикуляр к направлению![]() пересекаются в точкеВ. Следовательно,
точкаВявляется в этом положении
механизма мгновенным центром скоростей
и
пересекаются в точкеВ. Следовательно,
точкаВявляется в этом положении
механизма мгновенным центром скоростей
и![]() .
Это положение механизма называют
«мертвым». Найдем угловую скорость
шатуна
.
Это положение механизма называют
«мертвым». Найдем угловую скорость
шатуна
![]() =
0,5 рад/с.
=
0,5 рад/с.
На рис. 4.7,а показано распределение скоростей точек шатуна.
При угле поворота кривошипа j= 900скорости![]() и
и![]() направлены параллельно, а перпендикуляры
к ним пересекаются в бесконечности.
Следовательно, в данный момент времени
имеет место мгновенное поступательное
распределение скоростей, то есть все
точки шатунаАВимеют одинаковые
скорости, равные
направлены параллельно, а перпендикуляры
к ним пересекаются в бесконечности.
Следовательно, в данный момент времени
имеет место мгновенное поступательное
распределение скоростей, то есть все
точки шатунаАВимеют одинаковые
скорости, равные![]() ,
при этом угловая скорость шатунаwAB= 0 (рис. 4.7,б).
,
при этом угловая скорость шатунаwAB= 0 (рис. 4.7,б).
Пример 4.КривошипОА= 0,5м вращается с угловой скоростьюw0А= 10 рад/с и приводит в движение шатунАВ= 4 м.
Найти угловую скорость шатуна, скорости точек ВиС(АС= 2,5м), если угол поворота кривошипаj= 450иОА^АВ(рис. 4.8).
Решение
Так как кривошип ОАсовершает вращательное движение, то
![]()
Ш атунАВсовершает плоскопараллельное
движение. Найдем мгновенный центр
скоростей для данного положения шатуна
– точкуРна пересечении перпендикуляров
к скоростям точекАиВ,
восстановленных из этих точек. ТреугольникРАВ равнобедренный, при этомАВ = АР = 4
м.
атунАВсовершает плоскопараллельное
движение. Найдем мгновенный центр
скоростей для данного положения шатуна
– точкуРна пересечении перпендикуляров
к скоростям точекАиВ,
восстановленных из этих точек. ТреугольникРАВ равнобедренный, при этомАВ = АР = 4
м.
Найдем угловую скорость шатуна АВ
