2. Элементы теории надежности электронных систем

2.1. Термины и определения

Как указывалось во введении, надежность есть свойство системы (изделия) сохранять свои параметры в заданных границах в определенных условиях эксплуатации.

Из такого определения вытекает, что надежность как свойство является качественной характеристикой изделия, а количественные ее характеристики, по которым сравниваются разные изделия, являются за проявлениями этого свойства.

Следует отметить, что под системой в теории надежности понимают совокупность изделий, которые выполняют заданные функции и совместно обеспечивают общее функционирование всей системы. Часть системы, которая выполняет определенную функцию, называют элементом системы. Элементы электронной аппаратуры подразделяют на электрические (электрорадиодетали) и механические. К последним принадлежат панели, ручки управления, установочные, крепежные, и декоративные детали.

Пусть, например, рассматриваемым изделием является конденсатор фильтра. Этот конденсатор обеспечивает заданный коэффициент сглаживания фильтра (с достаточным запасом). С течением времени под действием физико-химических процессов, скорость протекания которых связана с климатическими факторами (влага, температура и т.п.), емкость конденсатора уменьшается. Это приводит к тому, что в некоторый момент времени коэффициент сглаживания фильтра становится меньше заданной величины. Работа фильтра становится ненадежной.

Итак, надежность прежде всего является функцией времени. Через некоторый интервал времени может произойти событие, после которого система не будет выполнять своих функций в заданном объеме, выходит из строя. Отказ - это событие, которое заключается в частичной или полной потере работоспособности изделия.

Отказы элементов системы можно распределить на три группы:

1) те, которые приводят к полному отказу системы;

2) те, что вызывают частичный отказ системы;

3) те, что не вызывают отказы системы.

Отказы систем бывают полные и перемежающиеся.

Полный отказ характеризуется тем, что пока не будут устранены причины, которые ее вызвали, использование системы невозможно. Для большинства простых систем полный отказ - явление невозобновляемое, например, перегорание непроволочного резистора, пробой полупроводникового диода или обрыв его внутренних выводов.

Перемежающийся отказ характеризуется кратковременным выходом системы из строя, после чего ее рабочие свойства восстанавливаются. Например, металлобумажный либо металлопленочный конденсатор очень часто восстанавливает свою электрическую прочность после кратковременного пробоя. Следует отметишь, что чаще всего перемежающиеся отказы вызываются плохими контактами. При этом они могут исчезать так не внезапно, как и появились.

По характеру изменения выходных параметров системы отказы делятся на постепенные и внезапные.

Постепенные отказы возникают в результате продолжительного процесса изменения параметров вследствие собственно работы и старения элементов системы. Выход значения параметра за установленные границы означает наступление отказа. Такие отказы в большинстве можно предусмотреть и принять меры к их предотвращению.

Внезапные отказы возникают скачкообразно из-за достаточно быстрого (практически – мгновенного) выхода из строя какого - либо элемента системы. Они имеют случайный характер, поскольку невозможно определить, когда именно тот или другой скрытый производственный дефект либо другая причина, вызвавшая отказ, проявит себя в виде обрыва, короткого замыкания или резкого изменения параметра.

Несмотря на существенное отличие характеров внезапных и постепенных отказов, между ними существует определенная взаимосвязь. Например, постепенный отказ может быть следствием нескольких внезапных отказов, которые происходят на более низком уровне связей в элементах системы. Таким образом, зависимый отказ возникает в результате другого отказа.

В работающей радиоэлектронной аппаратуре имеют место также независимые отказы, появление которых не зависит от неисправного или исправного состояния других элементов системы. Наконец, отказы могут быть предсказуемыми или случайными. Предсказуемые отказы не являются опасными, поскольку их легко предотвратить.

Множество факторов, которые в большинстве случаев определяют выходные параметры системы, обуславливают случайный характер отказов. Причем очень часто известны причины, которые вызвали отказ, но невозможно объяснить, чему она настала именно в данный момент времени. Случайные отказы вызывают наибольший интерес.

Системы промышленной электроники делятся на обслуживаемые и необслуживаемые, возобновляемые и не возобновляемые. В процессе эксплуатации обслуживаемых систем есть возможность контроля (а иногда и регулирования) исходных параметров.

Необслуживаемые системы имеют более низкую надежность сравнительно с обслуживаемыми, поскольку исключается возможность контроля и регулирования исходных параметров систем, а также их ремонта в процессе эксплуатации.

Возобновляемыми называют системы, которые после отказа можно починить. Они характеризуются наработкой на отказ - средним временем работы между двумя отказами, а также временами восстановления. Обе эти характеристики являются случайными и зависят от разных факторов, например, характера отказов, квалификации обслуживающего персонала и т.п. Имеются также другие показатели надежности, среди которых можно выделить [20]:

- К_г -коэффициент готовности;

- K_о.г -коэффициент оперативной готовности;

- Р(t_б.р) -вероятность безотказной работы при наработке t_б.р;

- Т_о -средняя наработка на отказ (наработка на отказ);

- t_б.р -наработка, в пределах которой вероятность безотказной работы изделия не ниже заданной;

- Т_ср -средняя наработка до отказа;

- λ -интенсивность отказов;

-γ -доверительная вероятность.

Невозобновляемые системы работают до первого необратимого отказа. Например, когда ракета в полете, нельзя ликвидировать неисправность ее электронной системы.

В период нормальной работы радиоэлектронной системы (срабатывание и старение элементов еще не наблюдается) возможные внезапные отказы, которые являются случайными. На этапе срабатывания и старения можно предусмотреть приближение отказа, однако сам момент отказа предугадать тяжело. Поэтому в большинстве случаев отказа в электронных аппаратах имеют случайный характер.

Судить о надежности электронного аппарата за одним отказом одного образца невозможно, поскольку отказы, обусловленные разными причинами, происходят в разные моменты времени. Более достоверные данные о надежности можно получить, наблюдая отказы множества образцов или одного образца на протяжении продолжительного времени (если при этом наблюдается большое количество отказов).

Таким образом, количественные показатели надежности элементов и систем, которые характеризуют массовые случайные явления, можно установить, воспользовавшись теорией вероятности, которая как раз и изучает массовые случайные события.

2.2. Краткие сведения по теории вероятностей

Теория вероятностей устанавливает закономерности для массовых случайных событий, т.е. для явлений, которые повторяются при многоразовых испытаниях. Событием называется любой факт, который происходит или не происходит в результате опыта.

События делятся на 3 основные группы:

1) возможные (достоверные) события, которые обязательно происходят в каждом испытании, при данных условиях;

2) невозможные события, которые никаким образом не могут состояться при определенных и известных условиях;

3) случайные события, которые невозможно предусмотреть в каждом отдельном испытании, т.е. неизвестно, когда они состоятся, а, возможно, вообще не состоятся в заданном интервале времени.

Несмотря на довольно неопределенный характер случайных событий, их нельзя отнести к категории беспричинных (при детальном рассмотрении событий почти всегда удается обнаружить причинно-следственные связи). Однако часто точно предугадать, когда возникнет такая их совокупность, за которой последует определенное событие, если состоится ли оно вообще, невозможно либо не целесообразно, поскольку требует значительных затрат, в том числе и финансовых.

Основными случайными событиями в теории надежности является отказ и отсутствие отказа.

Изучение причин отказов разных электронных устройств, других машин и механизмов, а также разработка мероприятий по уменьшению частоты отказов - главная задача надежности как науки и отрасли техники.

В теории вероятности (в теории надежности) там, где это возможно, стремятся оперировать не понятиями случайных событий, а случайными величинами.

Случайная величина - это такая переменная величина, которая в результате испытаний или опыта может принимать то или другое, заранее не (до опыта) не известное значение.

Случайные величины бывают дискретными и непрерывными.

Дискретная случайная величина – это такая величина, возможное значение которой на некотором конечном либо бесконечном интервале может принять некоторое определенное значение, отделимое от других возможных значений. Примером такой случайной величины может служить число, выпавшее на игральном кубике (не может выпасть число 1,3 или другое дробное, а только целое в диапазоне от 1 до 6). Другой пример – число младенцев, родившихся в роддоме за прошедшие сутки – также это число не может быть дробным.

Непрерывные случайные величины, в отличие от дискретных, обладают тем свойством, что их возможные значения непрерывно заполняют некоторый конечный либо бесконечный интервал. Например, непрерывной случайной величиной является измеренное в данный момент значение действующего напряжения фазы сети 380 В; время безотказной работы некоторого устройства и т.п.

Как уже известно, точно предугадать случайные события, а также случайные величины невозможно. Однако теория вероятностей, рассматривая не каждую случайную величину или событие отдельно, а всю их совокупность, позволяет охарактеризовать их с помощью математических методов.

Рассмотрим количественные соотношения.

Если при N испытаниях некоторое событие А состоялась М раз, можно найти W(A) - отношение M/N, которое называется частотой случайного события А:

(2.1)

С увеличением числа испытаний устанавливается устойчивость (регулярность) частоты появления события А. При этом, как показывают многочисленные эксперименты (практика), W(A) не очень отличается от некоторого постоянного положительного числа Р(А). На языке математики данный факт может быть выражен так:

(2.2)

Итак, можно предполагать, что для достаточно большого числа испытаний (в одних и тех же условиях) для любого случайного события А частота этого события будет приблизительно равняться Р, т.е.

(2.3)

Полученное число Р(А) называют вероятностью события А. Поскольку событие, которое нас интересует, есть отсутствие отказа, то речь идет о вероятности отсутствия отказа, или вероятности безотказной работы.

Таким образом, вероятность Р(А) есть некоторая физическая константа, которая численно в виде отношения числа появления этого события к общему числу испытаний показывает меру объективной возможности этого события. Такую вероятность появления случайного события называют статистической.

Наряду со статистической существует математическая вероятность появления случайного события Р(А)

(2.4)

где М — число случаев, которые оказывают содействие этому событию, а N— число всех равновозможных случаев. Равновозможными называют события, которые имеют одинаковую объективную возможность возникновения.

Для определения сущности статистической и математической вероятностей появления случайного события проведем эксперимент с бросанием игрального кубика, на гранях которого имеются цифры 1, 2, 3, 4, 5 и 6. Необходимо найти вероятность появления четного числа очков 2, 4 и 6. Тогда для математической вероятности М = 3, N=6 и P=3/6=0,5.

При определении статистической вероятности появления парного числа очков бросают игральный кубик, например, 10 раз. Пусть в результате этого четное число выпало 6 раз. Тогда P=6/10=0,6. Если в другой раз за 10 бросков четное число выпало 4 раза, то P = 4/10 = 0,4.

Итак, статистическая вероятность появления четного числа очков не равняется математической. С увеличением числа опытов статистическая вероятность сходится (а не приближается) к математической.

Вероятность возможного достоверного события принимают равным за 1, а невозможного за 0, вероятность появления случайного события находится в пределах от 0 до 1:

(2.5)

В классе случайных событий часто выделяют т.наз. практически невозможные события – такие события, вероятность наступления которых достаточно мала и ее величиной можно пренебречь. Такую достаточно малую вероятность называют уровнем значимости α; ее конкретное значение определяется сферой деятельности. В типовых случаях, не связанных с чрезмерными экономическими последствиями от события с малой вероятностью α, ее величина принимается на уровне 0,1 – 0,05. В более важных случаях, например, связанных с обеспечением безопасности жизнедеятельности человека, величина уровня значимости может быть значительно снижена, например, до уровня 0,01 либо еще ниже. Величину вероятности, дополняющей α до единицы, называют доверительной вероятностью 

=1- α (2.6)

Если вероятность появления события на определенном временном интервале будет достаточно мала (например, не более α), то такие события называют редкими. Ясно, что событие отказ правильно спроектированной системы – событие редкое. Одна из задач теории надежности – указать мероприятия, обеспечивающие оправданно малую величину вероятности события отказ на заданном временном интервале эксплуатации систем.

Следует особо отметить, что понятие вероятность в вышеприведенном смысле как объективной меры достоверности событий характерно исключительно для массовых, не уникальных событий и явлений. Так, в этом смысле не корректным является, например, вопрос – какова вероятность падения Луны на Землю? В этом вопросе предполагается конкретность и уникальность, а статистическая и математическая вероятности предполагают возможность повторения опытов многократно.

Приведем основные определения и соотношение, которые справедливые для случайных событий.

1. Два события А и В называют равносильными (А=В), когда после события А наступает событие В и наоборот.

2. События не равносильны, если событие А происходит только после события В (АВ).

3. Сумма двух событий А и В (А+В) означает, что состоится хотя бы одно из них.

4. Произведение событий А и В (АВ) означает, что они происходят одновременно.

5. Несколько событий называют несовместимыми, если их появление в одном опыте невозможно.

6. Противоположными называют такие два события А и , если их одновременное появление в одном опыте невозможна, но одно из них достоверно состоится.

7. Несколько событий называют независимыми, если появление одного или нескольких событий не зависит от появления других событий.

Рассмотрев основные соотношения для случайных событий, приведем правила вычисления вероятностей.

1. Для n несовместных событий, А₁,, А₂, ..., А_п вероятность появления однго из них равняется сумме вероятностей этих событий:

(2.7)

2. Вероятность совместного появления нескольких независимых событий равняется произведению вероятностей этих событий, т.е.

(2.8)

3. Из определения противоположных событий вытекает, что

(2.9)

2.3. Законы и числовые характеристики распределения случайных величин

Как отмечалось, случайная величина - это такая переменная величина, которая в результате испытаний может иметь то или другое значение. Закон распределения случайных величин (функция распределения, или просто распределение) связывает возможные значения случайной величины с вероятностями появления этих значений.

Закон распределения может быть задан различными способами – табличным, в виде графика, при помощи формул и т.д.

В качестве примера закона распределения дискретной случайной величины приведем достаточно распространенное распределение Бернулли, или биномиальное распределение.

Оно появляется в результате т.наз. схемы испытаний Бернулли. Пусть имеется достаточно большая (в пределе – бесконечная по количеству компонентов) совокупность компонентов (т. наз. генеральная совокупность), в состав которой входят компоненты, каждый из которых имеет один из двух признаков (например, годен либо не годен, резистор красного цвета либо зеленого, признака А либо ). При испытании из генеральной совокупности производится извлечение n компонентов (производится выборка из n компонентов, образующих т. наз. выборочную совокупность, или выборку объема n). Пусть известно, что при реализации выборки объема 1 (извлекается один компонент) вероятность того, что этот компонент обладает признаком А, составляет величину p, а вероятность противоположного события (этот компонент обладает признаком ), следовательно, будет равна величине q=1-p.

В выборке объемом n при такой схеме может появиться ровно m компонентов, с признаком А и n-m компонентов с признаком , где m – любое целое число от 0 до n включительно, т.е. случайное число. Вероятность того, что в такой выборке окажется ровно m компонентов, дает формула Бернулли:

(2.10)

где

(2.11)

- биномиальный коэффициент.

Как уже указывалось, закон распределения полностью характеризует случайную величину. Однако весьма часто для оценки распределения случайной величины вместо функции распределения достаточно знать лишь некоторые числовые характеристики этого распределения. Такими характеристиками являются, в частности, математическое ожидание, дисперсия и среднее квадратичное (квадратическое) отклонение случайной величины.

Математическим ожиданием М[Х] дискретной случайной величины Х называют сумму произведений всех возможных значений случайной величины на соответствующие этим значением вероятности:

(2.12)

где n – число возможных значений случайной величины;

- вероятность реализации i-го значения.

Смысл математического ожидания заключается в том, что оно приближенно равно среднему арифметическому значению нескольких наблюдаемых значений (реализаций) случайной величины (среднее значение реализаций тем ближе к математическому ожиданию, чем большее число испытаний было проведено). Наиболее вероятное значение реализации равно математическому ожиданию; математическое ожидание есть центр распределения. Ясно, что реализации случайной величины группируются вокруг математического ожидания.

Дисперсия D[Х] случайной величины Х есть численная мера степени разброса реализаций вокруг математического ожидания и для дискретной случайной величины определена как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

(2.13)

где - центрированная величина, которая представляет собой отклонение случайной величины X от ее математического ожидания.

По сути, дисперсия есть среднее значение квадрата отклонения случайной величины от математического ожидания. Некоторое неудобство при практическом использовании дисперсии заключается в том, что ее размерность равна квадрату размерности самой величины. Поэтому не менее часто в качестве меры рассеяния используют арифметический квадратный корень из дисперсии – т. наз. среднее квадратическое отклонение :

(2.14)

Для распределения Бернулли известно, что

; ;(2.15)

Если n велико (практически n>10), p мало (практически p<0,1) и при этом произведение np (т.е. в согласии с первым равенством 2.15, математическое ожидание) сохраняет постоянное значение (среднее число появлений событий в различных сериях испытаний остается неизменным), то результат вычислений по (2.10) будет мало отличаться от результата вычислений по т.наз. асимптотической формуле Пуассона:

(2.26)

где a=np.

Распределение Пуассона весьма часто используется при исчислении надежности электронных систем. С этим распределением тесно связано понятие потока событий – последовательности событий, которые наступают в случайные моменты времени. Потоком событий, в частности, является последовательность отказов элементов электронных систем.

Поток событий может обладать свойствами:

- стационарности (вероятность появления m событий на любом промежутке времени зависит только от числа m и от длительности t промежутка времени и не зависит от начала отсчета, а различные промежутки времени не пересекаются);

- отсутствия последствий, или независимости появления событий от наличия событий в непересекающихся промежутках времени);

- ординарности (появление двух и более событий за малый промежуток времени практически невозможно).

Такой поток событий называют простейшим или пуассоновским.

Интенсивностью потока  называют среднее число событий, которые появляются в единицу времени (например, за час). Тогда, при известном значении , можно найти среднее число событий за временной интервал от некоторого момента времени (начала отсчета) до момента прекращения испытаний длительностью t, или математическое ожидание числа событий на временном интервале длительностью t:

a= t (2.17)

Тогда, в соответствии с (2.16), можно получить:

_(2.18)

Выражение (2.18) есть распределение Пуассона для простейшего потока событий, является математической моделью для таких событий и показывает вероятность того, что на временном интервале длительностью от 0 до t произойдет ровно m событий. В частности, если трактовать отказ как событие, то m=0 будет означать отсутствие отказа на промежутке длительностью от 0 до t. Тогда из (2.18) при подстановке m=0 получим выражение для подсчета соответствующей вероятности (вероятности безотказной работы системы либо компонента при условии соблюдения условий простейшего потока событий):

_(2.19)

Распределение (2.18) по параметру m является дискретным, а по параметру t – непрерывным. Распределение (2.19) является непрерывным: возможные значения случайной величины – времени безотказной работы от момента постановки на испытание до отказа – непрерывно заполняют интервал от нуля до в общем случае до бесконечности. Подразумевая, что значение параметра m равно нулю, а функция распределения экспоненциально зависит от времени, такое распределение часто называют экспоненциальным:

_(2.19а)

Исчисление вероятности непрерывных случайных величин имеет некоторые особенности в сравнении с исчислением вероятности дискретных случайных величин. Действительно, число возможных значений непрерывной случайной величины бесконечно велико, а вероятность того, что она примет конкретное значение, исчезающее мала. Более конструктивным является другой способ задания возможных значений таких величин в связи с вероятностью их появления.

Функцию распределения F(t) непрерывной случайной величины можно задавать как функцию, связывающую вероятность P(t) появления случайной величины в некотором интервале, с параметрами границы этого интервала; при этом один из концов интервала фиксируют (например, 0 либо -), а другой конец является текущим, переменной величиной:

F(t)=P(0Tt) (2.20)

Тут T - обозначение случайной величины, t – правая граница интервала.

Очевидно, значения F(t)= P(t) принадлежат отрезку [0, 1]:

0≤ P(t)≤1 (2.21)

Функция F(t) – неубывающая либо невозрастающая. Например, вероятность отказа Q(t) компонента, поставленного на испытание, с течением времени может только возрастать в пределе до единицы (отказ компонента когда – ни будь произойдет), а вероятность безотказной работы P(t)– только падать (безотказная работа в конце концов когда – ни будь прекратится):

Q(t ₂)≥ Q(t₁); P(t₂)≤P(t₁) если t₂≥t₁ (2.22)

Рисунок 2.1 иллюстрирует вышесказанное на примере функций распределения Q(t) и P(t), определенных на интервале t[0, ]

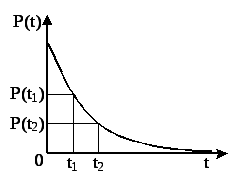
Рисунок 2.1. К определению функций Q(t) и P(t)

Если t₂≥t₁, то событие, заключающееся в том, что величина T примет значение, меньшее t₂, можно разделить на два несовместных: 1) T примет значение, меньшее t₁ с вероятностью P(0T t₁) и 2) T примет значение, удовлетворяющее неравенству t₁T t₂ с вероятностью P(t₁T t₂). В согласии с правилом сложения вероятностей (2.7) имеем

P(0T t₂)= P(0T t₁)+ P(t₁T t₂)(2.23)

Отсюда

P(t₁T t₂)= P(0T t₂)- P(t₁T t₂)= F(t₂)- F(t₁): (2.24)

вероятность того, что случайная величина примет значение, заключенное в интервале (t₁, t₂), равна приращению функции распределения на этом интервале.

Таким образом, зная поведение функции распределения на всем промежутке от нуля до бесконечности (либо от минус до плюс бесконечности) , е. во всем диапазоне, где эта функция определена, можно найти вероятность появления соответствующего события в любом интересующем интервале изменения случайной величины.

Описанную выше функцию распределения непрерывной случайной величины называют также интегральной функцией (либо интегральной формой представления) распределения.

Дифференциальная функция распределения непрерывной случайной величины (либо интегральная форма представления) определена как производная от интегральной функции:

(2.25)

Ее также называют плотностью распределения вероятностей случайной величины (функцией плотности вероятности).

Для плотности вероятностей можно записать

(2.26)

Если предположить, что прирост t бесконечно малый, то

(2.27)

Площадь под бесконечно малым участком кривой плотности распределения равняется приросту интегральной функции распределения. Очевидно, что площадь под участком кривой плотности распределения, ограниченным значениями х₁ и х₂, равняется приросту функции распределения на этом участке, т.е.

(2.28)

Используя выражение (2.24), получим

(2.29)

Выражение (2.29) позволяет именовать функцию P(t) интегральной функцией распределения, а p(t) - дифференциальной.

Таким образом, вероятность нахождения случайной величины на заданном участке (t₁, t₂) равняется площади под соответствующим участком кривой плотности вероятности.

Интегральная функция распределения вероятностей часто имеет начало в точке t = 0 (см. рис. 2.1). Тогда, полагая t₁ = 0, а t₂= t, получим

(2.30)

Если t →∞, то

(2.31)

поскольку F(∞) = l, a F(0)=0.

Если непрерывная случайная величина имеет как положительные, так и отрицательные значения, то

(2.32)

Выражение (2.32) физически трактуется так, что случайная величина обязательно примет какое-либо значение в пределах от -∞ до +∞.

Величина p(t)dt=f(t)dt) называется элемент вероятности.

Для непрерывной случайной величины, как и для дискретной, существуют понятия математического ожидания, дисперсии и среднего квадратического отклонения. Они определяются аналогично (см. (2.12), (2.13) и (2.14)), с тем отличием, что в этих выражениях суммы заменяются на несобственные интегралы, а значения вероятностей реализаций – на элементы вероятностей:

;

(2.33)

Так, для распределения Пуассона, описывающегося выражением (2.19а), выражения для плотности вероятности, математического ожидания, дисперсии и среднего квадратического отклонения будут выглядеть так:

; ;

;

(2.34)

Равенство математического ожидания и среднего квадратического отклонения является характерным признаком экспоненциального распределения.

В различных разделах теории вероятности и математической статистики, а также во многих отраслях техники (теории ошибок, измерений, надежности и др.) часто используется т.наз. нормальное распределение. Его функция плотности вероятности описывается двумя параметрами - математическим ожиданием а и средним квадратическим отклоненем  следующим образом:

(2.35)

Примерный график функции распределения f(t) представлен на рис. 2.2 – характерная колоколообразная симметричная кривая с максимумом в точке t=a, с общей площадью под кривой ( в диапазоне от - до +), равной 1 и степенью «приплюстности», зависящей от величины . Чем меньше величина , тем выше пик кривой.

Рисунок 2.2. График функции нормального распределения

Зная параметры распределения а и , можно определить вероятность появления реализации на любом интервале, например, от  до :

(2.36)

После замены переменных z=(t-a)/ и, соответственно, пределов интегрирования, (2.36) приводят к виду

, (2.37)

где

(2.38)

- интеграл Лапласа.

Интеграл Лапласа не берется в элементарных функциях, однако имеются подробные таблицы [19], позволяющие в функции параметра x найти соответствующие численные значения.

Нормально распределенные случайные величины широко распространены на практике. Этому факту дал объяснение А.М. Ляпунов в своей центральной предельной теореме (1901 г.): если на ход процесса, помимо некоторого не случайного фактора влияют большое число независимых факторов, влияние каждого из которых ничтожно мало, то результирующая случайная величина имеет распределение, близкое к нормальному. По закону, близкому к нормальному, распределена случайная величина – время наработки на отказ, если компонент находится на стадии своей работы достаточно длительно и наблюдается старение его составных частей (например, снижение прочности изоляции кабеля), обусловленное большим количеством мало учитываемых факторов (перепады температур, влажности, перемененная электрическая нагрузка и т.п.).

2.4. Параметры безотказности электронных компонентов

Параметры безотказности являются количественными показателями надежности, которыми пользуются для сравнения различных образцов элементов и устройств (систем), а также для задания необходимого уровня надежности таких элементов и устройств. Количественные показатели позволяют определить уровень надежности в процессе проектирования, а также контролировать его на производстве и в эксплуатации. Поскольку теория надежности использует как математический аппарат теорию вероятности, то основные показатели надежности также имеют вероятностный характер.

Как уже упоминалось выше, основной случайной величиной в теории надежности является время безотказной работы Т. Вероятность безотказной работы P(t), которая также является одним из основных показателей надежности, показывает вероятность того, что на протяжении времени безотказной работы t в системе при определенных условиях эксплуатации отказы будут отсутствовать

P(t)=P(0Tt) (2.39)

Очевидно, что 0< P(t)<1, поскольку Р(0) =1 (когда t =0, не случится ни одного отказа), а Р()=0 (когда t =, отказ становится достоверным событием).

Вероятность появления отказа элементов записывается так:

Q(t)=Q(0Tt) (2.40)

Поскольку отказ и отсутствие отказа - события противоположные, то, согласно уравнению (2.9), имеем

Q(t)=1- P(t) (2.41)

Для экспериментального определения P(t) ставят на испытание N_o элементов. Подсчитав количество элементов n(t), что вышли из строя на протяжении интервала времени t, получим статистическую вероятность

(2.42)

которая тем ближе к математической, чем большее число элементов N_0l были поставлены на испытания. Ориентируясь на это положение, знак приблизительного уравнения будем опускать. Если, например, P(t)=0,6, то это значит, что 60 % элементов, которые имеют данное значение вероятности безотказной работы, будут исправно работать, а 40 % откажут за время t.

Решая совместно уравнение (2.41) и (2.42), получим

(2.43)

Продифференцировав выражение (2.43) по времени t, получим скорость изменения вероятности безотказной работы во времени:

(2.44)

Скорость отказа элементов получим из выражения (2.44)

(2.45)

Поделим обе части уравнения (2.45) на N₀ — n(t):

(2.46)

В (2.46) учтено, что отношение числа N₀ — n(t) исправных элементов к общему числу элементов N₀, поставленных на испытание, есть вероятность безотказной работы элементов P(t).

Отношение скорости отказов элементов dn(t)/dt к числу исправных элементов, которые остались (N₀—n(t)) (см. уравнение (2.46)), представляет собой относительное изменение скорости отказов элементов и называется интенсивностью отказов (t), т.е.

(2.47)

 есть интенсивность потока событий отказ в соответствии с изложенным в разделе 2.3.

По сути, интенсивность отказов однотипных компонентов представляет собой среднее число отказов таких компонентов в единицу времени (например, час), приходящуюся на один компонент. Интенсивность отказов является одним из важнейших показателей надежности компонентов. Ее размерность – величина, обратная времени, например, час в минус первой степени (ч^-1).

На практике часто используется единица измерения интенсивности отказов – 1 FIT (Failure In Time):

1 FIT=110^-9 ч^-1 (2.48)

В выражении (2.47) для  подчеркивается тот факт, что в общем случае величина  является функцией времени (зависит от того, на каком промежутке жизненного цикла изделия производится определение численного значения ).

Проинтегрировав выражение (2.47) от 0 до t, получим:

(2.49)

Откуда

(2.50)

Формула (2.50) связывает вероятность безотказной работы элементов с интенсивностью их отказов для любого закона изменения интенсивности отказов во времени.

Закон изменения  во времени рассчитать невозможно, для его нахождения используют экспериментальные данные. Чтобы определить экспериментально  (t) в период нормальной работы элементов, необходимо во время опыта поддерживать постоянным число испытанных элементов N₀, заменяя элементы, которые вышли из строя. Тогда выражение 1/[N₀—n(t)] в формуле (2.47) можно заменить на 1/N₀. Если число элементов, которые вышли из строя во время опыта, увеличивается пропорционально времени, то выражение dn(t)/dt в той же формуле заменяют на n/t. Поэтому

(2.51)

Таким образом, экспериментально интенсивность отказов определяют как отношение числа элементов, которые отказали, к среднему числу элементов, которые исправно работают на протяжении времени t. Таким образом,  численно показывает долю (процент) элементов данного типа, которые вышли из строя за один час работы. Если, например, =110^-5, то это означает, что за 1 час работы выйдет из строя одна стотысячная часть элементов: соответственно за 100 часов работы — одна тысячная. Если таких элементов есть 100, то за тысячу часов работы можно ожидать выхода из строя одного элемента. Очевидно, когда значение N_ot небольшое, точность нахождения вероятности отказа элементов также небольшая. Поэтому для получения более или менее достоверных статистических данных относительно  необходимо подвергать испытанию большое количество элементов продолжительное время. Именно так поступают ведущие производители компонентов, имеющие развернутую систему управления качеством своей продукции.

Типичная зависимость интенсивности отказов электронных компонентов и систем от времени, подтверждающаяся практикой, показана на рис.2.3. Для этой кривой характерные три периода.

Рисунок 2.3. Типовая зависимость интенсивности отказов от времени

В начальный период жизненного цикла компонента (область 1, или период приработки, период ранних отказов) интенсивность отказов велика, когда очевидно ненадежные элементы (или элементы со скрытыми дефектами – результат брака) быстро выходят из строя. Этот период характерен спадом частоты отказов. Его длительность и скорость спада зависят, в основном, от конструкции изделия, свойств примененных материалов и уровня технологии.

К моменту времени t₁ интенсивность отказов уменьшается и начинается период 2 — нормальной работы (нормальной эксплуатации, статистических отказов). Статистические отказы в средней части графика (область 2) имеют практически неизменную интенсивность. Практика показывает, что на интервале нормальной работы превалируют внезапные отказы.

С течением времени (после момента t₂) интенсивность отказов начинает возрастать - начинается период 3. Для него характерно превалирование постепенных отказов, связанных со старением и выработкой ресурса компонента. Начало периода 3 соответствует окончанию срока службы изделия, дальнейшая эксплуатация, как правило, не целесообразна. Для силовых ключей истечение ресурса сопровождается лавинообразным ростом теплового сопротивления кристаллов, разрывом электрических связей, потерей управляемости [24].

Для периода нормальной работы (интервал времени t₁— t₂), когда отказы большей частью имеют внезапный характер, а (t)=const, уравнение (2.50) приобретает вид

(2.52)

что характерно для простейшего (пуассоновского) потока событий.

Период приработки (0—t₁), который обычно составляет приблизительно 50—100 ч, можно исключить предварительными тренировками изделий в нормальных или жестких условиях перед передачей покупателю. Это часто практикуется для ответственной аппаратуры. Так поступают ведущие производители компонентов, особенно – относительно дорогостоящих мощных силовых полупроводниковых приборов, осуществляя 100% выходной контроль своих изделий.

Постепенные отказы, которые превалируют в третьем периоде, при правильной постановке профилактических работ можно прогнозировать. Для таких отказов, как указывалось выше, для потока событий отказ характерно распределение, близкое к нормальному.

Выражение (2.52) является базовым (основным) для оценки надежности компонента на интервале нормальной работы. Для того, чтобы была возможность им воспользоваться, необходимо иметь сведения о величине интенсивности отказа в конкретном режиме работы.

Под режимом работы понимают совокупность т. наз. дестабилизирующих факторов (например, температуры окружающей среды, влажности, давления, механических нагрузок типа вибраций с определенной частотой и ускорением, ионизирующего излучения и т. п.), отличающий данный конкретный режим работы от номинального (базисного) для данного компонента. На надежность также весьма существенно влияют электрические нагрузки компонента (напряжение, ток, частота), а также температурные нагрузки, обусловленные выделением тепловой энергии в приборе в процессе работы. Под базисным (в смысле значения =₀) понимают значение интенсивности отказов в номинальном электрическом режиме (если это особо не оговорено) в т. наз. лабораторных условиях (температура окружающей среды 25С, атмосферное давление 760 мм ртутного столба, относительная влажность до 60%, отсутствие вибраций).

Значение интенсивности отказов элементов также сильно зависит от их конструкции и технологии изготовления. Однако даже высококачественные элементы быстро выходят из строя, если они работают в электрических режимах и условиях эксплуатации, которые не допускаются техническими условиями. В жестких условиях эксплуатации, а также в режиме перегрузки интенсивность отказов резко возрастает.

Отличие  от его номинального значения ₀ учитывают при помощи поправочных коэффициентов – коэффициента уровня надежности К_ун (обусловлен уровнем технологии изделия, уровнем контроля технологического процесса, количеством контролируемых выходных параметров изделия), коэффициента условий (жесткости, окружающей среды) К_у учитывающий совокупность климатических, широтно – географических и прочих эксплуатационных режимов (в том числе связанных с наличием вибраций, внешних температурных и других воздействий), коэффициента электрических нагрузок К_н, коэффициента температурных нагрузок К_t (обусловленных выделением тепловой энергии в приборе в процессе работы). Могут аналогично (введением соответствующих коэффициентов) учитываться также и другие факторы. Выражение для , учитывающее вышеприведенные коэффициенты, есть математическая модель расчета интенсивности отказов: и в общем случае выглядит так:

(2.53)

где λ_0j – исходная (базовая) интенсивность отказов j-го потока отказов;

m – количество независимых потоков отказов составных частей изделия;

К_ij – коэффициент, учитывающий влияние i-го фактора в j-м потоке отказов;

nj – количество факторов, учитываемых в j-ом потоке отказов.

Для компонента, учитывая вышесказанное, (2.53) можно переписать так:

=₀ К_ун К_у К_н К_t (2.54)

Аналогичным образом рекомендуется, в частности, в ряде стандартов по определению надежности (см., напр., [21]), учитывать изменение  в режиме нормальной работы под влиянием различных дестабилизирующих факторов. Так, для силовых полупроводниковых компонентов может быть использована модель вида [22]

_P=_B(_E_Q_A_S _R_C _T) (2.55)

где _P=₀ = базисное значение интенсивности отказов;

_E – фактор окружающей среды;

_Q – фактор качества компонента;

_A - фактор токовой нагрузки на компонент;

_S - фактор нагрузки напряжения на компонент (стресс – фактор);

_R – фактор допустимой предельной токовой нагрузки;

_C – фактор особенности конструкции;

_T – фактор температурных нагрузок.

Очевидно, в согласии с (2.54) и (2.55), можно записать:

К_ун=_Q;К_у=_E;К_н=_A_S _R_C;К_t=_T(2.56)

Фактор качества _Q (уровень надежности) К_ун учитывают в случае, если значение ₀ для данного компонента не известно, но известно это значение для аналогичного по функции, но отличающегося степенью контроля. Например, в Советском Союзе существовало несколько уровней качества компонентов – т. наз. «приемки»: «приемка 3», «приемка 5», «приемка 7», «приемка 9». Изделия с более высокой группой приемки подвергались более «жесткому» контролю, с контролем большего числа параметров, не выборочному контролю, а 100% и т.д. Приборы более высокого уровня качества маркировались особо. Например, биполярные транзисторы высокого уровня качества маркировались цифрой и буквой: 2Т…; обычного уровня – буквами: КТ… . Для приборов высокого уровня качества («приемка 7», «приемка 9», для приборов зарубежного производства - т. наз. military, government and space – для военного применения, для правительственных заказов и для использования в космических приложениях) либо при известном значении ₀ полагают К_ун=1. Для приборов среднего уровня качества («приемка 5», industry – общепромышленное применение) при неизвестном значении для них ₀ , но известном значении ₀ для аналогичных, но высокого уровня качества полагают К_ун=10. Для приборов относительно низкого уровня качества («приемка 3», commercial) в таких случаях устанавливают К_ун=10 при известном значении ₀ для аналогичных с уровнем качества industry и К_ун=100 при известном значении ₀ для аналогичных с уровнем качества military, government and space.

В лабораторных условиях устанавливают К_у=1. В других условиях К_у1. Ориентировочные значения коэффициента жесткости в качестве справки представлены в Таблице 1.

Таблица 1. Примерные значения коэффициента условий (жесткости) К_у

Условия эксплуатации	Величина Ку
Нормальные условия	2,5 – 10
Наземная аппаратура	10 – 13
Морские и речные суда, корабли	13 – 25
Автомобили	25 – 30
Железнодорожный транспорт	30 – 40
Высокогорье	40 – 50
Самолеты	50 – 100
Ранние образцы ракет	100 – 200
Современные ракеты	200 – 500 (до 1000)

Электрический режим, в котором находится компонент, характеризуется коэффициентом нагрузки К_н, что представляет собой отношение действительного (реального) нагрузки к номинальному для данного элемента согласно техническим условиям, т.е.

_(2.57)

где Z — уровень действующей нагрузки; Z_nоm-уровень номинальной электрической нагрузки.

Критерием меры нагрузки считают электрический параметр, влияние которого на работоспособность элемента является решающим. Например, для резисторов таким параметром является рассеиваемая мощность, для конденсаторов - рабочее напряжение и мощность потерь (определяется действующим значением переменной составляющей напряжения, частотой и тангенсом угла потерь), для биполярных транзисторов - мощность, которая рассеивается на коллекторе, для диодов - максимальное обратное напряжение и среднее значение и действующее значение прямого тока. При этом формулы для определения коэффициентов нагрузки обычно имеют вид:

- для транзисторов К_н= Р_С/Р_Сnom , где Р_С и Р_Сnom – фактическое и номинальное значение мощности, рассеиваемой на коллекторе транзистора;

- для диодов К_н=U_R/U_RRM, где U_R и U_RRM – амплитуда обратного напряжения диода и его номинальное значение (обычно – предельно допустимое значение повторяющегося обратного напряжения);

- для резисторов К_н=Р_R/Р_Rnom ,где Р_R и Р_Rnom – фактическое и номинальное значение мощности, рассеиваемой в резисторе;

- для конденсаторов К_н=U_С/U_Сnom

Для силовых компонентов преобразователей часто отдельно учитывают в К_н не только мощностную составляющую и составляющую напряжения, но и токовую составляющую (см. 2.56).

Значение К_н влияет на фактическое значение интенсивности отказа компонента: с уменьшением значения К_н значение  падает примерно пропорционально, и при этом увеличивается интервал времени нормальной работы компонента.

На рис. 2.4 показаны кривые, которые отображают зависимость интенсивности отказов от времени в случае использования элементов в условиях разгрузки (К_н<1, кривая 1) и граничной (К_н=1 кривая 2) -эксплуатации. В разгрузочном режиме интенсивность отказов имеет меньшее значение. При этом несколько увеличивается продолжительность этапа приработки, однако более длительным становится период нормальной работы, а срабатывание (старение) элементов наступает значительно позднее.

Рисунок 2.4. Влияние коэффициента нагрузки К_н на зависимость интенсивности отказов от времени: 1 – при К_н<1; 2 - при К_н=1

На практике бывают случаи, когда коэффициент нагрузки следует оценивать другими электрическими величинами. Например, высокоомные резисторы чаще всего работают в условиях рассеивания мощностей, которые являющихся небольшой частью номинальных, а приложенное к ним напряжение близкое к предельно допустимым значениям и потому оказывает значительное влияние на отказы резисторов. В таких случаях режимы резисторов следует характеризовать отношением напряжений, а не мощностей.

Для обеспечения оптимальных показателей надежности обычно для силовых полупроводниковых приборов коэффициент нагрузки по напряжению устанавливают на уровне около 0,5. Так, для IGBT модулей АИН для асинхронного электропривода при напряжении АИН примерно 600 В (выпрямленная трехфазная сеть 380 В 50 Гц) предельно допустимая величина напряжения транзистора принимается 1200 В, а для преобразователей с повышенным уровнем надежности – на уровне 1700 В.

При напряжениях силовых полупроводников, отличных от рекомендованных (например, отличающихся от 600 В при предельном напряжении прибора 1200 В) можно для нахождения поправочного коэффициента _S пользоваться эмпирической формулой [22]:

_S=V_s^2,43, V_s=U_R/U_RRM для диодов;

_S=V_s^1,9, V_s=U_D/U_DRM для тиристоров;

_S=V_s^1,4, V_s=U_C/U_CM для IGBT (2.57а)

Для коэффициента нагрузки по току различают таковой для среднего тока, длительно протекающего через прибор (_A - фактор токовой нагрузки на компонент) и для импульсного (аварийного) тока (_R – фактор допустимой предельной токовой нагрузки). Первый влияет на величину средней мощности потерь и, следовательно, на величину температуры перехода, а второй – на надежность при отработке перегрузки. Последнее важно, в частности, для IGBT модулей, поскольку при коммутации больших токов, заметно (до двух – пятикратной по отношению к классификационному значению предельно допустимой величины среднего тока прибора) возрастает падение напряжения на транзисторе, что может привести к недопустимому росту температуры перехода даже при малой длительности токовой перегрузки. Повышение температуры может привести к возникновению эффекта защелки из-за наличия в структуре прибора паразитного тиристора. Коммутация тока перегрузки может приводить к появлению перенапряжений на выключающемся приборе из-за наличия паразитной (монтажной) индуктивности в контуре коммутации при высокой скорости спада тока коллектора. Для ограничения перенапряжений при коммутации токов перегрузки, помимо минимизации контурной индуктивности, используют замедление скорости выключения – технология active clamping, реализованная в драйверах приборов ведущих производителей [23]. Обычно коэффициент нагрузки по длительному току устанавливают на уровне не более 0,8, а по предельной токовой нагрузке – на уровне не более 2, принимая меры по ограничению перенапряжений.

Практика показывает, что интенсивность отказов весьма существенно зависит от температуры перехода T_j. Температура перехода - наиболее интегральный параметр, определяющий правильность выбора элемента, расчета его рабочих режимов и теплового анализа системы охлаждения. Соблюдение рекомендаций по обеспечению тепловых характеристик не только является залогом надежной работы; величина Tj непосредственно влияет на интенсивность отказов и срок службы изделия [24].

За базовую модель зависимости интенсивности отказов от температуры принимается уравнение Аррениуса. В 1889 году Сванте Аррениус вывел это уравнение эмпирически, изучая влияние температур на скорость превращения сахарозы, за что был удостоен Нобелевской премии в области химии. Это уравнение приближенно описывает многие деградационные процессы и отказы многих электрических и электронных компонентов, в том числе полупроводниковых приборов, интегральных микросхем, резисторов, конденсаторов и т.п. из-за таких явлений, как ионный дрейф, диффузию примесей, образование интерметаллических соединений, ползучесть, кристаллографические микроперестроения конструкционных материалов [25]. Уравнение Аррениуса (2.58) в равной степени хорошо описывает появление отказов приборов при воздействии повышенной температуры, как в период приработки, нормальной работы, так и на периоде старения:

(2.58)

где E_a - энергия активации;

T₁ и T₂ - соответственно нормальная и повышенная температуры (T₁ - 25С);

P₁ и P₂ - рассеиваемые мощности на переходе;

₁ и ₂ – тепловые сопротивления зоны переход–окружающая среда.

k – постоянная Больцмана.

При фиксации температуры перехода на уровнях T₁ и T₂ полагают ₁ и ₂ равными нулю.

Величину энергии активации ведущие производители полупроводниковой техники устанавливают на уровне 0,7 - 0,8 эВ. Именно эту величину 0,7 эВ фирма Analog Devices использует в расчётах интенсивности отказов. Фирма Microchip в расчёты закладывает величину 0,6–0,7 эВ [25]. Величина энергии активации 0,8 эВ примерно соответствует правилу "20 градусов". В соответствии с правилом "20 градусов" принимают, что скорость отказов увеличивается примерно вдвое при увеличении температуры на 20°С. Рисунок 2.5 иллюстрирует это [24].

Рисунок 2.5. Примерная зависимость относительной величины интенсивности отказов от температуры.

На практике учет интенсивности отказов от температуры учитывают также при помощи эмпирических зависимостей. В качестве примера приведем выражения для коэффициента К_t=_T, рекомендуемого для использования фирмой Мицубиси [22]:

для диодов;

для тиристоров

для полевых транзисторов (2.59)

Из вышесказанного следует, что интенсивность отказов компонентов является сложной функцией температуры и коэффициента (коэффициентов) нагрузки. Часто эти зависимости представляют в виде семейств характеристик, аргументом которых является температура, а параметром – коэффициент нагрузки. Такие зависимости в виде примера для пленочных резисторов и керамических конденсаторов приведены на рис. 2.6 и 2.7 [27].

Рисунок 2.6. Зависимость интенсивности отказов керамических

конденсаторов от температуры при различных коэффициентах загрузки

Следует отметить, что очень часто данные об интенсивности отказов имеют ориентировочный характер, что затрудняет получение достоверных результатов для вероятности безотказной работы. Более того, интенсивности отказов разных элементов в реальных условиях эксплуатации могут значительно отличаются от приведенных данных. Поэтому речь может идти лишь об оценках, более или менее адекватных.

На характеристики надежности силовых полупроводниковых приборов в раде случаев влияет специфический для этих приборов фактор, связанный с цикличностью тепловой нагрузки на прибор, комплексно именуемый циклоустойчивостью, или стойкостью к термоциклированию.

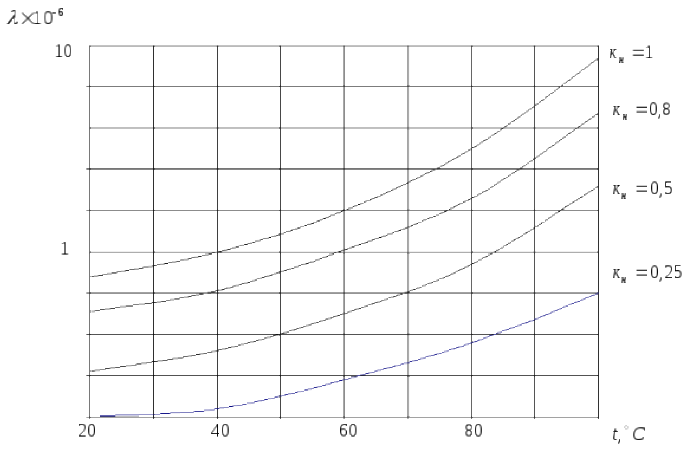
Рисунок 2.6. Зависимость интенсивности отказов пленочных резисторов

от температуры при различных коэффициентах нагрузки

Под термоциклом понимают временной интервал, для которого характерен перепад (градиент) температуры перехода полупроводника прибора. Поскольку материал полупроводника (кремния) имеет определенный коэффициент температурного расширения, а сам кремниевый чип крепится на подложку (керамическую DCB – Direct Bonded Copper – плату с медными шинами, нанесенными диффузионными методами) с несколько другим коэффициентом температурного расширения, при термоциклировании возникают механические напряжения в кристалле. Неоднократное повторение термоцикла (нагрев – остывание) приводит к усталостному разрушению компонентов силового модуля, нарушению герметизации и т.п. и в результате - и отказу. Основные причины отказа – отслоение выводов кристаллов от медных шин и разрушение паяных соединительных слоев. Косвенно о приближении чипа к граничному состоянию можно судить по повышению до допустимой величины напряжения коллектор – эмиттер IGBT [28]. Особенно актуальны проблемы термоциклирования в приложениях, связанными с транспортными средствами – в электротранспорте, в автоэлектронике.

Предположим, что в течение 15 лет транспортное средство подвергается в среднем двум холодным пускам в день, когда охлаждающая жидкость разогревается от 5 до 105 °С и охлаждается до исходного состояния. Таким образом, за время эксплуатации все составные части электронного модуля привода испытывают воздействие 10 тыс. термоциклов с градиентом 100 °С.

Температура «пассивного» или внешнего термоцикла является базовой, к ней добавляется «активный» термоцикл, образуемый за счет тепловыделения силовых ключей. Анализ типовых характеристик движения показывает, что силовые элементы преобразователя транспортного привода за время работы испытывают в среднем 3 млн активных термоциклов с градиентом 40 °С [28].

В 1991 году была принята европейская программа оценки технических решений TechnologyAssessment. В рамках данной программы Совет по науке Швейцарии сформулировал требования по энергосбережению и надежности изделий силовой электроники, а также требования к системным и информационным технологиям LESIT (Leistungselektronik, Systemtechnik undInformationstechnologie). В процессе реализации программы LESIT проводились многочисленные испытания надежности силовых модулей различных производителей.

Цифры, полученные в ходе тестов, позволили создать математическую модель, описывающую связь количества термоциклов до отказа N_f с перепадом температуры и средней температурой кристалла T_m = T_jmin + ΔT_j/2. Эта модель, конечно, является приблизительной, она не может принять во внимание все процессы, происходящие в структуре модуля при воздействии термомеханических напряжений. Тем не менее, при создании модели основные физические механизмы были учтены: зависимость пластической деформации от ΔT и влияние T_m на свойства материалов. Полученные графики (рисунок 2.7) предоставляют возможность определить, что между количеством термоциклов до отказа силового модуля и градиентом температуры существует степенная зависимость. Выяснилось, что кривые, отображающие данную зависимость при различных значениях T_m, расположены почти параллельно, что позволяет описать их в соответствии с законом Аррениуса:

(2.60)

Где А=640 (специфическая константа);

=-5;

Q=7,8 10-4 Дж/моль;

R=8,314 Дж/мольК (газовая постоянная)

На рис. 2.7 показаны результаты испытаний одиночного модуля IGBT с номинальным током 300 А и напряжением 1200 В, проведенных по программе LESIT. Тесты выполнялись при различных значениях средней температуры кристалла T_m и градиента температуры ΔT_j .Цель испытаний — выяснение влияния параметров T_m и ΔT_j на стойкость силового модуля к термоциклированию. Испытания проводились при следующих условиях:

- ток нагрузки — 240–300 А;

- время нагрева t_on — 0,6–4,8 c;

- время охлаждения t_off — 0,4–5 c;

- критерий отказа — увеличение напряжения насыщения V_CEsat на 5%.

Поскольку при тестах использовались «короткие» термоциклы, все испытуемые модули отказали в результате отслоения проводников и разрушения слоя металлизации. Важным следствием испытаний стало подтверждение факта, что средняя температура является для определения надежности не менее важным параметром, чем ее перепад.

Данная описательная модель считается достаточно достоверной в рамках проведенных LESIT экспериментов, то есть при 30K < ΔT < 80K и периоде цикла, не превышающем 10 с. Однако для реальных транспортных режимов эксплуатации характерны медленные термоциклы, образуемые изменяемыми условиями нагрузки и внешней среды. Как было сказано, термоциклы длительностью 30–60 с приводят в первую очередь к развитию усталостных процессов в паяном соединении DCB-керамики и медного основания силового модуля. Поэтому ведущие производители (Semikron, Westcode) для подобных приложений начинают применять модули не паяной, а прижимной конструкции (следует отметить, что мощные тиристоры и диоды прижимной конструкции – так наз. циклоустойчивые - давно и успешно применяются).

Рисунок 2.7. Результаты испытаний по программе LESIT

Если данные о циклоустойчивости компонента неизвестны, то, поскольку термоциклирование тесно связяно с особенностями конструкции, для учета таких особенностей иногда вводят фактор особенности конструкции _C (см. (2.55)). Так, для приборов в металлостеклянном и пластмассовом корпусе величины этого коэффициента (при недоступности соответствующих данных) в [22] значения коэффициента _C рекомендуется принимать 1 и 2 соответственно.

Таким образом, данные по термоциклированию силовых модулей определяют среднее число термоциклов изделия при определенных параметрах термоциклирования, а при известной длительности термоцикла (среднего времени между двумя термоциклами) позволяют найти среднее время наработки на отказ T₀ силового модуля как произведение средней длительности термоцикла на среднее количество термоциклов до отказа.

Среднее время наработки на отказ T₀, часто именуемое также средним временем безотказной работы, наряду с интенсивностью отказов  также является одним из важнейших параметров безотказности компонента. Его синонимом является величина, именуемая «среднее время между отказами». В зарубежной литературе для этого понятия используется аббревиатура MTTF (Mean Time To Failure) - среднее время до наступления отказа. Для ремонтируемого изделия существует понятие среднего срока службы до ремонта (MTTR — Mean Time To Repair) и MTBF (Mean Time Between Failure — средняя наработка на отказ). В общем случае MTBF= MTTF+ MTTR. Для неремонтируемых изделий, к каким относятся силовые компоненты преобразователя (силовые модули, конденсаторы, резисторы, интегральные микросхемы драйверов и т.п.), принимают MTBF= MTTF [24].

Численные значения T₀ и  на интервале нормальной работы компонента ( =const) связаны между собой простым соотношением:

T₀ =1/ (2.61)

Действительно, вероятность отказа элементов Q(t) является интегральной функцией распределения вероятности отказа. Производная от интегральной функции распределения f(t) представляет собой функцию плотности вероятности отказа, т.е.

(2.62)

Если известная функция плотности вероятности отказа f(t)=q(t), то, согласно первому выражению в (2.33) можно определить математическое ожидание отказа, т.е. среднее время безотказной работы элемента T₀:

(2.63)

Поскольку время не может быть отрицательным, то границы интегрирования в выражении (2.63) следует заменить, т.е.

(2.64)

Учитывая уравнение (2.41) и (2.62), получим

(2.65)

Проинтегрируем выражение (2.65) по частям:

(2.66)

и учтем, что когда t=, Р(t)=0 (отказ становится событием достоверным), или же

(2.67)

Из уравнения (2.66) получим

(2.68)

После подстановки выражения (2.50) в (2.68) имеем

(2.69)

Поскольку чаще всего вызывает интерес период нормальной работы элементов, когда превалируют внезапные отказы, а (t)= const, то в этом случае

(2.70)

Вероятность безотказной работы элементов в этом случае

(2.71)

Из уравнений (2.71) вытекает, что когда t=T₀, P(t) =e^-1=0,37. В этом случае лишь 37 % элементов из общего количества, поставленных на испытание, к моменту времени t=T₀ от начала испытаний продолжают исправно работать, а 63 % откажут (вероятность отказа равняется 0,63 (2.41)). Итак, для надежной работы элементов на интервале от нуля до t необходимо выполнение неравенства t<<T₀.

Из выражения (2.71) и аналогичного (2.52) вытекает определение такого параметра, связанного с надежностью, как минимального времени наработки на отказ, или минимальной наработки. Это интервал времени t_б.р (t_мин) , в пределах которого вероятность безотказной работы изделия не ниже заданной, достаточно высокой, величины. В качестве такой достаточно высокой вероятности обычно принимают величину этой вероятности 0,9 либо 0,95. Саму же вероятность, выраженную в процентах, именуют гамма-процентным ресурсом . Задавшись величиной Р(t) в (2.71), равной, например, 0,9, найдем значение t_мин относительно T₀:

t_мин/T₀=ln Р(t_мин)=ln0,90,1 (2.72)

С понятием гамма-процентного ресурса (и понятием минимальной наработки на отказ как интервала времени, в течение которого компонент безотказно работает с высокой вероятностью) тесно связано понятие профилактики как комплекса мероприятий по продлению ресурса изделия. Суть профилактики заключается в том, что в системе на основании анализа значений интенсивностей отказов компонентов выделяют группу компонентов, обладающих наименьшей надежностью. Задаваясь допустимой величиной вероятности безотказной работы компонента Р(t) (гамма-процентного ресурса), при известном значении из выражения (2.71) определяют время достижения компонентом состояния, соответствующего заданной вероятности безотказной работы. По истечению этого интервала времени компонент следует заменить на новый, еще не побывавший в эксплуатации.

Из трех важнейших параметров безотказности, которые были рассмотрены выше (вероятность безотказной работы, среднее время наработки на отказ, интенсивность отказов), как начальную и основную характеристику обычно используют интенсивность отказов, согласно которой рассчитывают среднее время наработки на отказ и вероятность безотказной работы. Как отмечалось, интенсивность отказов элементов является статистической оценкой. Значение ₀ не может быть рассчитано пользователем теоретически и определяется производителем компонента на основе данных эксплуатации или же специально проведенных испытаний.

В Таблице 2 приведены типовые значения интенсивности отказов для некоторых компонентов электроники, в том числе силовой.

Изделия первого поколения аппаратур электронной техники отмечались большими значениями интенсивности отказов. Даже специальные электронные лампы высокой надежности, которые были изготовлены для трансатлантического подводного кабеля, имели интенсивность отказов не менее 210^-7 1/ч.

Проблема надежности подталкивала специалистов к поискам усилительного электронного прибора более надежного, чем электронная лампа. Трудно сказать, которая из проблем в большей мере стимулировала изобретение транзистора — проблема массы и габаритов или проблема надежности. Так или иначе, в среднем для транзисторов была достигнута интенсивность отказов около10^-7 1/ч. В ряде случаев интенсивность отказов достигала 10^-8 и даже 10^-9 1/ч. Приблизительно такими же цифрами характеризуется и интенсивность отказов паяных соединений в электронной аппаратуре. Это очень показательная цифра: транзистор, предстающий собой сложный электронный прибор, и паяный контакт имеют примерно одинаковую надежность (тут следует заметить, что высокая надежность пайки достигается при использовании современных способов изготовления паяных соединений – при пайке волной, при использовании технологии спекания на специальных паяльных станциях, при автоматизации процесса пайки).

С появлением интегральной электроники можно было предположить, что надежность интегральной микросхемы будет во столько раз хуже надежности

Таблица 2. Значения интенсивности отказов некоторых компонентов

Наименование	010-6 ч-1	Примечание
Резисторы постоянные непроволочные металлодиэлектрические	0,048	Экспоненциальный рост в функции температуры и мощности рассеивания
Резисторы постоянные непроволочные металлизированные	0,037	Экспоненциальный рост в функции температуры и мощности рассеивания
Резисторы постоянные непроволочные композиционные пленочные	0,03	Экспоненциальный рост в функции температуры и мощности рассеивания
Резисторы постоянные непроволочные композиционные объемные	0,035	Экспоненциальный рост в функции температуры и мощности рассеивания
Конденсаторы пленочные полипропиленовые силовые MKV B258XX	0,05 - 0,5	При температуре менее 40 С; Увеличивается вдвое при росте температуры на 10 С
Конденсаторы пленочные полипропиленовые фильтровые пост. напряжения MKР B258XX	0,001	При температуре менее 40 С
Дроссели фильтров	0,002	Увеличение в 20 раз при температуре 85 С
Тиристоры	0,02 – 0, 06	Увеличение в 50 раз при номинальном напряжении и температуре 100 С
Диоды силовые выпрямительные низкочастотные	0,001 – 0, 004	Увеличение в 50 раз при номинальном напряжении и температуре 100 С
IGBTмодули SKiiP без драйвера	0,06 – 0,246	В зависимости от числа кристаллов в модуле
IGBT модули SKiiP с драйвером	1,113 – 2,276	В зависимости от числа кристаллов в модуле
Конденсаторы электролитические Epcos, Vishay	2,5	При температуре менее 40 С, рост вдвое при росте температуры на 10 С; рост в 8 раз при увеличении напряжения от 0,5 до 1 от номинального
Кабели, провода	(0,0003 – 0,0012)/м

отдельного (дискретного) полупроводникового прибора, сколько эквивалентов таких приборов она включает в себя. Кроме того, в состав интегральной схемы входят точечные контакты (сварные или паяные) и пассивные элементы, которые, в свою очередь, должны повысить интенсивность отказа микросхем, и, следовательно, уменьшить их надежность.

Однако оказалось, что интегральные микросхемы имеют надежность, которая существенно превышает ожидаемые исходя из такой точки зрения значения. Интенсивность отказов большинства микросхем достигает 10^~7 - 10^-8 1/ч, , а в ряде случаев - 10^-9 1/ч, т.е. приближается к надежности, достигнутой для дискретных полупроводниковых приборов и даже превосходит их [25] (и это несмотря на то, что в современных больших интегральных микросхемах может быть интегрировано до нескольких десятков или даже сотен миллионов элементарных компонентов!). Это объясняется такими причинами:

1. В разработке интегральных микросхем принимают участие специалисты, которые хорошо знают физические процессы в полупроводниках, методы построения принципиальных схем и знакомы с физическими проблемами надежности. Схемные решения, которые не выгодны с позиции надежности, изымаются в процессе проектирования.

2. Условия изготовления всех диодов, транзисторов в пределах одного кристалла, достаточно однородного по структуре полупроводникового материала, практически одинаковы. Это обеспечивает высокое качество электрических параметров полупроводниковых приборов, а также хорошую повторяемость идентичных параметров.

3. Диоды и транзисторы, резисторы, конденсаторы в составе интегральных микросхем работают в более легких электрических режимах (низкое значение коэффициента нагрузки), что существенно уменьшает их интенсивность отказов.

4. Для межэлементных соединений микросхемы точечные контакты типа пайка или сварка не применяются. Такие соединения, (не являющиеся сварными или паяными), являются основой развития современной микроэлектроники, поскольку позволяют не только получить высокую плотность монтажа, но и продвинуться еще на один-два порядка по пути снижения интенсивности отказов.

5. Компоненты микроэлектроники, особенно производства ведущих производителей, изготавливаются на высокотехнологических предприятиях с тщательным многостадийным межоперационным контролем, в процессе которого выбраковываются (исключаются из технологического процесса) чипы с дефектами. Изделия подвергаются выходному контролю, часто полному (100% -му).

В силу вышесказанного, для повышения надежности компонентов следует устанавливать оптимальные значения коэффициентов нагрузки, использовать компоненты с высоким уровнем качества, обеспечивать температурный режим компонента, отдавать предпочтение решениям, использующим интегральные микросхемы.

2.5. Параметры безотказности электронных систем

Любая радиоэлектронная система (ЭС) состоит из компонентов, объединенных единым алгоритмом функционирования. Сама система может рассматриваться как «черный ящик» и для него, как и для отдельного компонента (точнее, для большого количества однотипных систем), может быть применено понятие интенсивности отказа системы _с. В этом смысле определение величины _с принципиально не отличается от принципов нахождения величин интенсивностей отказов отдельных компонентов. Однако использование выражений (2.50), (2.52), (2.61) - (2.71) при подстановке =_с. возможно в том случае, когда в формуле (2.42) и далее N_o будет означать количество испытанных систем. Однако, испытывая сложные системы, воспользоваться большим значением произведения N_ot часто вообще невозможно, например, для дорогостоящих систем, общее количество которых не велико и может составлять несколько единиц. На практике в результате испытаний определяют интенсивность отказов элементов, из которых состоит система. Последнее практически всегда возможно.

Для нахождения вероятности и среднего времени безотказной работы ЭС определим связь между этими параметрами и интенсивностью отказов элементов, которые составляют систему. При этом будем считать, что рассматриваемая система такова, что выход из строя (отказ) хотя бы одного элемента системы означает отказ всей системы. Такие системы называются не резервированными в отличие от систем, выход из строя какого – либо компонента не обязательно означает выход какого-либо параметра системы за пределы, устанавливаемыми технической документацией. Кроме этого, сделаем предположение (оно соответствует действительности в случае, когда элементы работают до отказа системы в условиях установившегося режима), что отказ элемента есть событие случайное и независимое.

Пусть система состоит из m типов элементов с числом элементов каждого типа n₁, п₂,..., п_т. Вероятность безотказной работы элементов каждого типа — P₁(t), P₂(t), .. , Р_m(t).

На основе правила о вероятности совместного появления нескольких независимых событий можно записать:

(2.73)

Выражая вероятность безотказной работы каждого типа элементов через интенсивность отказов, т.е.

(2.74)

и подставив эту систему уравнений в (2.73), получим

(2.75)

Выражение (2.75) позволяет определить вероятность безотказной работы сложной не резервированной системы для любого закона изменения интенсивности отказов элементов во времени.

Если система находится на этапе нормальной работы, то в случае _i=const выражение (2.75) имеет вид

(2.76)

Согласно (2.76), как и для компонента (см. (2.71)), так и для системы в случае _i=const можно записать

(2.77)

где _с - интенсивность отказов системы.

Сравнивая выражения (2.76) и (2.77), получим

(2.78)

где _с – интенсивность отказа системы, вычисляемая как сумма интенсивностей отказов всех компонентов, входящих в систему.

Среднее время безотказной работы T_0c системы и вероятность ее безотказной работы на интервале времени от начала эксплуатации до текущего момента t тогда составят

(2.79)

Выражения (2.77) - (2.79) позволяют оценить надежность не резервированной ЭС любой сложности через интенсивности отказов элементов, составляющих систему.

2.6. Методика расчета надежности системы при внезапных отказах

Расчет надежности радиоэлектронного изделия состоит в определении основных количественных характеристик надежности: вероятности безотказной работы на протяжении заданного интервала времени, среднего времени безотказной работы и др. Заданный интервал времени зависит от назначения устройства и условий его работы. Исходными данными для расчета надежности являются известные средние значения интенсивности отказов элементов, которые содержит изделие. Выражения, которые связывают основные показатели надежности радиоэлектронных изделий как систем с интенсивностями отказов, были получены ранее (см. п. 2.5)

Исходными данными для расчета надежности является электрическая схема устройства и значения интенсивностей отказов компонентов системы (в том числе печатных плат, соединений и т.п.).

Целесообразна такая последовательность расчета надежности:

1. Анализируют принципиальную схему устройства с точки зрения влияния отказов отдельных элементов на работоспособность всего устройства. Если выход из строя любого из элементов приводит к отказу всего устройства, то соединение элементов в схеме в смысле надежности - последовательное. В этом случае приступают к выполнению пункта 2.

2. Группируют все элементы устройства в группы с примерно одинаковыми значениями интенсивности отказов _i .

3. Для каждой такой группы определяют произведение п_i_i.

4. Рассчитывают интенсивность отказов устройства _с как сумму произведений п _i_i (с согласии с по выражением (2.78)).

5. Определяют среднее время безотказной работы (среднее время до первого отказа) по первой формуле (2.79).

6. Согласно второму уравнению (2.79) находят вероятность безотказной работы устройства P(t) (гамма-процентный ресурс) для упомянутого интервала времени t и, при необходимости – минимальное время наработки на отказ в согласии с (2.72).

Расчет надежности электронной системы обычно проводят в два этапа.

На первом этапе производят предварительный расчет и его проводят, как правило, на этапе эскизного проектирования. Его целью является получение сравнительной оценки различных вариантов построения системы и одним из критериев выбора того или иного варианта могут быть численные значения каких-либо показателей надежности. Поскольку на этом этапе предлагаются и сравниваются еще не проработанные окончательно схемные решения, доступна лишь относительно грубая оценка интенсивностей отказов компонентов, без учета влияния коэффициентов нагрузки, конкретных значений показателей электромагнитных нагрузок компонентов, их потерь мощности, температуры и т.п. Поэтому на данном этапе рекомендуется для сравниваемых вариантов задавать одинаковые типовые значения ₀ интенсивностей отказов однотипных компонентов (конденсаторов, резисторов, дросселей, силовых ключей, драйверов и т.п.), вовсе не учитывать особенностей электрических режимов (коэффициенты нагрузки элементов считают равными 1) и влияние прочих дестабилизирующих факторов, в том числе температуры и параметров окружающей среды.

На этом этапе целесообразно выявлять компоненты (группы компонентов), в наибольшей степени влияющие на надежность разрабатываемой электронной системы в целом. Такие компоненты называют «отстающими» - величина их интенсивности отказов имеет наибольшее значение, именно для них в первую очередь следует в ходе проектирования принимать меры по повышению надежности (см. ниже). В «идеальной» с точки зрения надежности системе основные компоненты (группы компонентов) имеют примерно одинаковую надежность и по окончании определенного времени почти все выходят из строя (имеют примерно одинаковый ресурс работы).

На втором этапе проводят окончательный (уточненный) расчет надежности. Его делают, когда уже рассчитана электрическая часть электронной системы, известны электромагнитные и тепловые (мощностные) нагрузки компонентов, имеются экспериментальные данные окончательного варианта изделия. Поэтому в окончательном расчете имеется возможность найти реальные значения коэффициентов нагрузки и параметры внешних воздействий, (температура, влага, давление, механические нагрузки и др.)и скорректировать базисные значения интенсивностей отказов компонента с учетом реальных условий эксплуатации.

Интенсивности отказов элементов для окончательного расчета надежности определяют с помощью моделей (см., например, выражения (2.53)- (2.56)), графиков типа рис. 2.6), которые позволяют получить значения корректировочных коэффициентов как функцию коэффициента нагрузки, температуры и параметров внешнего действия. Часто, при эксплуатации изделия в условиях отапливаемых помещений (commercial), выражение (2.54), являющееся основой для подсчета величины интенсивности отказа компонента, записывают в виде

(2.80)

где  — интенсивность отказов для данного коэффициента нагрузки и температуры; ₀— номинальная интенсивность отказов, которая соответствует единичному значению коэффициента нагрузки при температуре 25 °С. Тогда

(2.81)

Интенсивность отказов системы _с подсчитывают как сумму произведений:

(2.82)

где _i — температурный и нагрузочный коэффициент і-го элемента, n – количество элементов і-го типа, m – число групп компонентов с различными значениями ₀ (однотипных резисторов, конденсаторов и т.п. с близкими значениями ₀ в рабочем режиме).

Рекомендуется данные по значениям интенсивностей отказов свести в таблицу (пример показан в виде Таблицы 3).

При отсутствии необходимых данных (графических либо других) следует пользоваться известными значениями номинальных интенсивностей отказов аналогичных приборов. Часто бывает тяжело учесть действие всех внешних факторов из-за отсутствия необходимых данных. Поэтому в окончательном расчете надежности в этих случаях коэффициенты нагрузок берут близкими по значению к верхней для данных условий границе.

Таблица 3. Пример оформления таблицы для подсчета

интенсивности отказов системы

Название группы компонентов	Условное обозначение	Количество элементов	Интенсивность отказов в номинальном режиме 0, 10-6 ч-1	Коэффициент нагрузки Кн	Температура, С	Поправочный коэффициент i	Интенсивность отказов і-го элемента в рабочем режиме i, 10-6 ч-1	Интенсивность отказов в і-й Группы элементов niii, 10-6 ч-1
1. Транзисторы
2. Конденсаторы
…
								Итого с

2.7. Способы повышения надежности ЭС

2.7.1. Характерные отказы компонентов

Выход из строя изделия обусловлен недостаточной надежностью элементов, ошибками при проектировании и производстве, а также неправильной эксплуатацией. В большинстве случаев отказ аппаратуры происходит из-за отказа одного или нескольких компонентов, которые входят в ее состав. Поэтому обеспечение надежности аппаратуры сводится, главным образом, к обеспечению надежной работы компонентов. Рассмотрим основные причины отказов компонентов, из которых состоят устройства промышленной электроники.

Отказы контактных и пассивных компонентов.

Резисторы составляют до 30-45 % от общего числа элементов аппарата, а на них приходится приблизительно 13-20 /₀ отказов [30].

Выход из строя резисторов обусловлен чаще всего перегоранием и обрывом резисторного слоя, который проводит ток, а также вследствие нарушение контакта между внешним выводом и этим слоем. Иногда наблюдается резкое изменение сопротивления резистора. Преимущество с точки зрения надежности имеют объемные резисторы перед пленочными, низкоомные - перед высокоомными. Отказы пленочных резисторов чаще всего происходят из-за обрыва вывода.

Проволочные резисторы переменного сопротивления более надежные, чем непроволочные, отказы которых чаще всего наступают из-за нарушения скользящего контакта ползунок – проводящий слой.

Конденсаторы, как и резисторы, довольно широко применяются в аппаратуре. Однако отказы конденсаторов происходят значительно реже, чем резисторов. Отказы конденсаторов происходят большей частью из-за пробоя диэлектрика. Причиной таких отказов являются недостатки в конструкции и скрытые производственные дефекты, например, воздушные включения, которые оказывают содействие развитию ионизационных процессов. Это приводит к уменьшению электрической прочности конденсатора. Причиной отказа конденсатора может быть нарушение герметичности.

Электролитические конденсаторы имеют невысокую надежность. Очень отрицательно реагируют они на колебания температуры (перегрев, переохлаждение) и перегрузку. Расположение электролитического конденсатора вблизи источника тепла будет способствовать высыханию электролита, повышению тангенса угла потерь и дополнительному нагреву конденсатора.

Отказы трансформаторов и дросселей случаются вследствие обрыва или перегорание проводов, а также вследствие уменьшение электрической прочности изоляции. Основными причинами таких отказов является плохое крепление трансформатора, небрежная намотка, плохая защита от влаги, тяжелый тепловой режим.

Реле обычно выходят из строя из-за обрывов обмоток, пробоя изоляции, обгорания контактов. И хотя удельный вес реле в радиоаппаратуре небольшой (кроме устройств автоматики), высокая интенсивность их отказов заставляет разработчиков и конструкторов особенно тщательно подходить к вопросам обеспечения правильного рабочего режима и установки их в аппарате.

Разного рода переключатели, панели, штепсели отказывают, главным образом, из-за нарушения контактов или механических повреждений.

Отказы полупроводниковых приборов. Внезапные отказы полупроводниковых приборов (как в дискретном, так и в интегральном исполнении) обусловлены, главным образом, недостатками конструкции или нарушениями технологического процесса. Постепенные отказы являются следствием недостатков и нарушений технологии изготовления таких приборов.

Внешние проявления внезапных отказов интегральных микросхем, .транзисторов, тиристоров, силовых двухслойных диодов проявляются в виде обрывов внешних и внутренних выводов, пробоя и короткого замыкания p-n переходов и подзатворного диэлектрика полевых приборов, трещин кристаллов.

Причинами обрывов или перегораний внутренних выводов могут быть или неоднородности толщины провода, который соединяет электроды с внешними выводами, или нарушение режима пайки или термокомпрессии выводов внутри корпуса с p-n -переходами. Короткие замыкания между электродами полупроводниковых приборов является следствием попадания вглубь корпуса посторонних металлических частиц вследствие выплесков металла, когда сваривают ножки приборов с корпусом.

Отличие температурных коэффициентов линейного расширения кремния, арсенида галлия и электродных материалов при термоциклировании и работе в условиях отрицательных температур приводит к образованию микротрещин в кристаллах и, как следствие, к резкому увеличению обратного тока и уменьшению напряжения пробоя.

Постепенные отказы полупроводниковых приборов как событие выхода одного из параметров за заданные пределы наблюдаются значительно чаще, чем внезапные. Медленное ухудшение параметров полупроводниковых приборов (дрейф параметров) связанно с изменениями состояния поверхности кристалла полупроводника, а также с нарушением условий нормальной теплоотдачи. Однако следствием такого события, как правило, является необратимое нарушение работоспособности, т.е. в конце концов – внезапный отказ.

Проникновение в корпус и через слой лака молекул кислорода и воды в результате нарушения герметизации приводит к изменению поверхностной проводимости кристаллов. Это вызывает увеличение обратных неуправляемых токов и токов потерь. Изменяется коэффициент передачи по току транзисторов, крутизна прямой передачи полевых приборов. Тиристоры могут включаться без поступления сигнала управления.

Недостаточная чистота и точность обработки теплоотводящей поверхности, плохое смачивание припоем поверхности кристалла вызывает ухудшение условий нормальной теплоотдачи. В результате возможен перегрев p-n -перехода даже при небольших мощностях рассеяния, который в конечном итоге приводит к тепловому пробою.

Наличие посторонних включений в кристаллической решетке вызывает отказы такого же рода, как и плохая герметизация. Однако эффект их значительно слабее.

Изучение причин отказов разнообразных электронных устройств, а также разработка мероприятий по уменьшению частоты отказов – актуальная задача теории о надежности.

2.7.2. Способы повышения надежности ЭС на этапе проектирования

Основы надежности ЭС должен закладывать разработчик и конструктор на этапе проектирования. В процессе проектирования, который включает в себя разработку принципиальной электрической схемы и конструкции устройства, следует учитывать факторы, которые влияют на надежность системы:

1. Количество и качество электрорадиодеталей, других элементов конструкции, материалов, которые применяются в устройстве.

Увеличение количества компонентов увеличивает интенсивность отказов устройства как системы (см. (2.82)), что уменьшает вероятность безотказной работы устройства в целом. Итак, на этапе проектирования необходимо использовать простейшую схему, которая имеет наименьшее количество деталей, но отвечает требованиям технического задания. К этому вопросу необходимо подходить творчески, поскольку в отдельных случаях некоторое усложнение схемы не уменьшает надежность, а наоборот, способствует ее повышению. Так, например, введение дополнительных элементов защиты, автоматической настройки и контроля усложнит схему, однако существенно повысит ее надежность.

Весьма желательно (см. п. 2.4) максимальное использование в решениях интегральных микросхем, которые не только заменяют большое количество дискретных компонентов, но и сами по себе имеют высокую надежность.

Точка пайки также является при расчете надежности элементом ЭС. Очевидно, что число точек пайки, особенно при использовании в системе интегральных микросхем, существенно превышает общее число прочих компонентов. Поэтому качество паяных соединений должно быть высоким – так, чтобы суммарный вклад точек пайки в интенсивность отказов системы не сделал паяные соединения «отстающим» элементом. Следует применять прогрессивные способы пайки и монтажа (пайка волной, поверхностный монтаж с использованием соответствующих типов корпусов компонентов, спекание вместо пайки и т.д.). В Таблице 4 [29] приведены базисные значения интенсивности отказов для некоторых способов электрических соединений.

Таблица 4. Значения базовой интенсивности отказов

различных видов соединений

Вид соединения	λ0·,10-8, 1/ч
Ручная пайка ЭРИ без накрутки	0,13
Ручная пайка ЭРИ с накруткой	0,007
Пайка ЭРИ волной	0,0069
Сварка	0,0015
Обжимка (опрессовка)	0,012
Беспаяное соединение накруткой	0,00068
Скрутка	0,026

Примечание: для пайки не используется понятие коэффициента нагрузки

Повысить надежность системы можно, применяя компоненты с более высоким уровнем надежности, с более высоким диапазоном рабочих температур. Компоненты, декларируемые как компоненты с высоким уровнем надежности (government and space, military, приемка 7, 9), проходят более тщательный выходной контроль по большому числу параметров и в результате имеют существенно меньшую величину ₀. В специальной литературе [21,29] приводятся данные по параметрам моделей высоконадежных компонентов высокого уровня качества.

2. Режимы работы компонентов.

Ясно, что даже самый надежный компонент быстро откажет, если будет работать в не допустимом для него режиме (например, при температуре кристалла, превышающей предельно допустимую). Поэтому надо стремиться к уменьшению коэффициентов нагрузки, выбирая радиодетали с предельно допустимыми значениями напряжений, токов и мощностей, превышающими эти параметры реальной схемы (см. п. 2.4).

Следует заметить, что снижение коэффициентов нагрузки компонентов влечет за собой повышение стоимости компонентов и системы в целом. Это характерно для силовых компонентов преобразователей. Например, цена IGBT модуля на определенный класс напряжения примерно пропорциональна величине классификационного тока, поскольку предельный постоянный ток прибора производители наращивают, соединяя параллельно кристаллы с площадью около 1 см², что влечет за собой увеличение количества кремния в приборе и стоимость. Для снижения коэффициента нагрузки конденсатора по величине переменной составляющей его напряжения требуется увеличения эквивалентной емкости конденсаторной батареи и, следовательно, пропорциональное увеличение цены. Поэтому требуемое значение коэффициента нагрузки компонента и, следовательно, требуемое значение соответствующего показателя надежности, должно быть обосновано исходя из задаваемого соотношения цена – качество (под последним можно понимать величину показателя надежности).

3. Схемное решение и конструктивное оформление.

То же самое устройство (компонент) может давать не одинаковый эффект по надежности при различных схемных решениях преобразователя, хотя при его проектировании использовано одинаковое количество элементов одних и тех же типов. Существенно зависит надежность электронного устройства и от конструктивного оформления в процессе разработки. Например, расположение электролитических конденсаторов вблизи деталей, которые сильно нагреваются (трансформаторы, силовые полупроводниковые приборы), приводит к быстрому высыханию электролита и, как следствие, к быстрому выходу из строя компонента. Неудачная трассировка печатной платы (например, расположение печатных проводников входных цепей драйверов вблизи силовых компонентов с большими производными токов) может приводить к сбоям в работе системы и возникновению аномальных и аварийных режимов при протекании которых возможны отказы силовых приборов.

4. Стандартизация и унификация.

Стандартизированные и унифицированные изделия изготовляются специализированными предприятиями, где хорошо отработана технология изготовления. Они проверены практикой, а потому более надежны. Ведущие производители постоянно совершенствуют качество компонентов, в условиях конкуренции со стороны менее известных производителей вынуждены подтверждать высокое качество своей продукции.

На этапе проектирования необходимо также тщательно проанализировать возможные условия эксплуатации; грамотное конструктивное решение вопросов тепло - и влагозащиты, защиты от ударов, вибраций, повышенного и пониженного давления и других факторов существенно повышают надежность изделия.

5. Использование резервирования.

Одним из важнейших способов повышения надежности изделий электроники является резервирование - введение избыточности в систему, т.е. компонентов, которые не являются принципиально необходимыми для осуществления функции устройства. Цель введения резервирования – повышение надежности работы изделия. В случае отказа компонента либо блока отказавший компонент либо блок исключаются из работы, и функцию отказавших принимают на себя резервные компоненты (блоки). Ясно, что резервирование влечет за собой повышение массы, габаритов, цены изделия и должно быть технически целесообразно. Подробное рассмотрение разновидностей и характеристик резервированных электронных систем не входит в цели данной работы. Отметим, что у резервированных систем, обладающих на определенном интервале времени большей величиной вероятности безотказной работы в сравнении с не резервированными, с течением времени вероятность безотказной работы падает сильнее, чем у не резервированных [31]. Поэтому системы длительного периода работы, к которым в большинстве случаев следует отнести преобразовательные системы для асинхронного электропривода, выполняются как не резервированные. Надежность таких систем повышают выше перечисленными способами (1 – 4).

Из вышесказанного, а также анализа данных по интенсивности отказов входящих в преобразователь для электропривода компонентов, следует, что отказы интегральных микросхем системы управления, пассивных компонентов системы управления (в том числе печатных плат) существенно менее вероятны, чем отказы силовых компонентов преобразователя. Поэтому при анализе последствий отказов (аварийных режимов) следует прежде всего проанализировать электромагнитные нагрузки не отказавших силовых компонентов. Аварийные нагрузки на силовые компоненты преобразователя могут приводить к отказам этих компонентов (зависимые отказы). Поэтому целью анализа может быть получение значений токов и напряжений силовых компонентов в аварийных режимах. Знание этих характеристик позволяет выработать рекомендации по выбору (корректировке) номинальных значений соответствующих параметров компонентов и способах воздействия на не вышедшие из строя активные (управляемые) элементы, предотвращающих дальнейшее увеличение электромагнитных нагрузок и тем самым минимизировать последствия возникновения аварийных режимов. Вопросам методологии такого анализа посвящен следующий раздел.