Бесконечно большие величины:

Определение 7: Переменная величина у называется бесконечно большой, если при своем изменении она становится и в дальнейшем остается по абсолютной величине больше любого наперед заданного положительного числа N:

|у| > N

Замечание: Бесконечно большая величина у не может стремиться ни к какому пределу А, т.к. при своем изменении переменная у по абсолютной величине перерастает абсолютную |А| всякого числа А, и разность у – А, увеличиваясь по абсолютной величине при дальнейшем изменении у, не может оказаться величиной бесконечно малой.

Говорят, что предел положительной бесконечно большой величины у равен плюс бесконечности (Lim y = + ), предел отрицательной бесконечно большой величины у равен минус бесконечности (Lim y = - ), предел бесконечно большой величины, не сохраняющий при своем изменении определенного знака, равен бесконечности (Lim y = ).

Связь между бесконечно большой и бесконечно малой величинами.

ТП 4: Если у – величина бесконечно большая, то - бесконечно малая.

ТП 5: Если у – величина бесконечно малая, то - бесконечно большая, у ≠ 0.

Например:

1. Вычислить: Lim

х → 1+

Решение:

Т.к. числитель и знаменатель дроби являются бесконечно большими величинами при х→ , то пределов числителя и знаменателя не существует,

поэтому разделим каждое слагаемое числителя на знаменатель:

, тогда

= (1 + ) = + = 1 + 5 x Lim = 1 + 5 x 0 =1,

x→+

т.к дробь при х → +∞ является бесконечно малой величиной и следовательно ее предел равен нулю.

Ответ: Lim = 1.

х → 1+

2. Найти: Lim

х →

Решение:

Числитель и знаменатель выражения, стоящего под знаком предела при х→ являются бесконечно большими величинами, поэтому для того, чтобы можно было применить теоремы о пределах, предварительно разделим числитель и знаменатель дроби на старшую степень х:

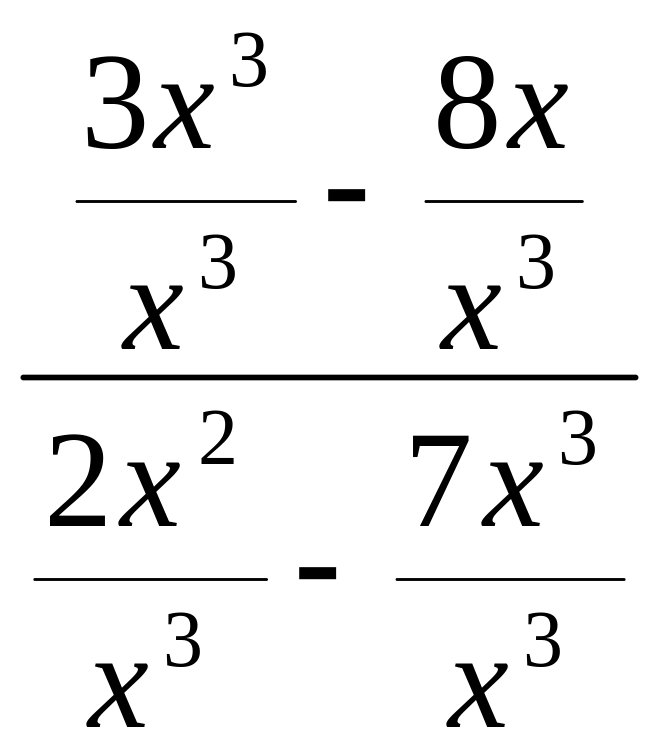Lim = Lim = Lim = .

х → х → х →

Т.к. под знаком предела стоит дробь, то нужно выяснить, отличен ли от нуля предел знаменателя:

Lim = Lim - Lim 7 = 2 x Lim - 7 = 2 x 0 – 7 = -7,

x→∞ x→∞ x→∞ x→∞

т.к. при безграничном возрастании х является величиной бесконечно малой и следовательно Lim = 0. Предел знаменателя отличен от нуля, следовательно:

x→∞

= = = = = -

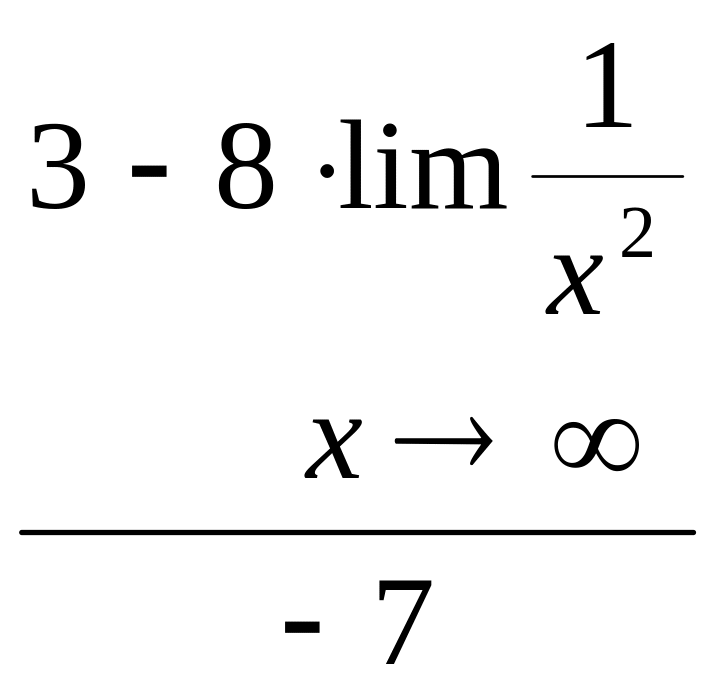Ответ: Lim = -

х →

Задание 1.

1. Lim ;

x→+∞

1.02 Lim ;

x→+∞

1.03 Lim ;

x→ -2

1.04 Lim ;

x→ 4

1.05 Lim ;

x→ 2

1.06 Lim ;

x→ -2

1.07 Lim (х² – 4х + 5);

x→ 5

1.08 Lim ;

x→∞

1.09 Lim ;

x→ 2

1.10 Lim .

x→