Лабораторная работа № 7 линейная фильтрация

Цель работы: закрепление теоретических знаний связанных с фильтрацией сигналов

Необходимые теоретические сведения

Выходной сигнал фильтра можно найти, используя функцию filter.

Она реализует алгоритм цифровой фильтрации, соответствующий транспонированной структуре фильтра (direct form II transposed)

y= filter (b, a, s);

где b и a – векторы коэффициентов числителя и знаменателя передаточной функции фильтра; s – вектор входного сигнала; y – вектор выходного сигнала. Рассчитав выходной сигнал, можно построить графики входного и выходного сигналов:

plot (t, s, ‘r’, t, y, ‘g’)

Входной сигнал будет отображён непрерывной линией красного цвета, а выходной – непрерывной линией зелёного цвета.

При использовании функции stem лучше вывести графики отдельно:

subplot (2,1,1) stem (t, s, ‘.r’) subplot (2, 1, 2) stem (t, y, ‘.b’)

Цифровую фильтрацию можно осуществить как операцию свёртки входного сигнала и импульсной характеристики фильтра. Для этого сначала нужно получить импульсную характеристику фильтра:

h= impz (b, a);

где b и a – коэффициенты полиномов числителя и знаменателя передаточной функции, h – вектор отсчётов импульсной характеристики. Количество отсчётов рассчитывается автоматически и зависит от поведения импульсной характеристики. Для явного задания количества расчётных точек n нужно ввести оператор:

h= impz (b, a, n);

Для вывода графика импульсной характеристики не нужно указывать выходной параметр и ставить точку с запятой:

impz (b, a)

Рассчитав импульсную характеристику, можно найти выходной сигнал фильтра методом свёртки:

y= conv (s, h);

где s – вектор входного сигнала, h – вектор импульсной характеристики, y – вектор выходного сигнала.

Далее следует построить графики входного и выходного сигналов.

Еще один способ фильтрации в частотной области с использованием быстрого преобразования Фурье (БПФ) выполняется следующим образом. В соответствии со спектральным методом спектр выходного сигнала равен произведению спектра входного сигнала и комплексной частотной характеристики фильтра. Спектр вычисляется путём применения к сигналу, заданному в виде последовательности отсчётов, дискретного преобразования Фурье (ДПФ). В MatLab алгоритм ДПФ применяется в форме БПФ (FFT –Fast Fourier Transform). Для осуществления фильтрации в частотной области задаются операторы (подразумевается, что сигнал s, частота дискретизации Fs, а также коэффициенты фильтра b и a определены ранее:

K= freqz (b, a, 512); S= fft (s, 1024); Y= S(1:512) .*K; y= ifft (Y);

Нужно следить, чтобы суммарное количество отсчётов сигнала s и импульсной характеристики h = impz (b, a) не превышало 1024. В противном случае нужно использовать функцию fft, задавая более высокую размерность преобразования. Тогда большее количество точек n надо задавать при расчёте частотной характеристики фильтра:

K = freqz (b, a, n);

где n = N/2, где N – размерность БПФ. Помимо графиков сигналов можно вывести спектры входного и выходного сигналов и частотную характеристику фильтра:

f = (0:511)/512*(Fs/2); subplot (3,1,1) stem (f, abs(S(1:512))) subplot (3,1,2) plot (f, abs(K)) subplot (3,1,3) stem (f, abs(Y(1:512)))

Вместо функции stem можно использовать функцию plot, тогда получим непрерывные спектры. Если имеется необходимость совместить все три графика, то можно использовать операторы hold on и hold off вместо операторов subplot. Для различения графиков нужно задать различный цвети (или) тип линии.

Блочную фильтрацию с помощью БПФ (сигнал разбивается на блоки по N отсчётов, где N – размерность БПФ) можно также реализовать, используя функцию fftfilt:

y = fftfilt (h, s, N);

где h – вектор импульсной характеристики фильтра, s – вектор входного сигнала, N – размерность БПФ.

Рассмотрим пример. Пусть необходимо смоделировать с помощью программы MatLab сложный сигнал следующего вида:

S(t)=Y(t)+X(t)+d(t),

где Y(t)=A·sin(t)-синусоидальный сигнал;

X(t) – треугольный импульс;

d(t) – белый Гауссовский шум.

Для генерации случайной последовательности с равномерным законом

распределения вероятностей служит функция rand, с нормальным законом распределения – функция randn.

Fs= 1e3; t=0:1/Fs:1; sigma= 2; d= sigma * randn ( length(t), 1); sn= s+d;

С помощью дискретных фильтров Чебышева первого (пульсации в полосе пропускания) и второго (пульсации в полосе задерживания) рода выделить из сложного сигнала треугольный, отфильтровав, таким образом, синусоидальную составляющую и белый Гауссовский шум с нулевым математическим ожиданием и дисперсией ϭ²=4.

t=0:0.1:25; % определение временного интервала y=0.5*sin(25*t); % определение синусоидального сигнала x=4*sawtooth(t,0.5); % определение треугольного сигнала d=0.1*randn(251,1); % задание белого Гауссовского шума plot(t,x,t,y,t,d), grid % вывод 3-х составляющих сигнала на экран xlabel ('Время'); % подпись оси Х («Время») ylabel ('Амплитуда'); % подпись оси Y («Амплитуда»)

s=x+y+d; % синтез сложного сигнала plot(t,s), grid; % вывод сложного сигнала на экран xlabel ('Время'); % подпись оси Х («Время») ylabel ('Амплитуда'); % подпись оси Y («Амплитуда»)

Построим АЧХ фильтров. В случае цифрового фильтра wn задается в нормированном виде по отношению к частоте Найквиста:

[b,a]=cheby1(6,0.06,4/14); % определение параметров фильтра % Чебышева первого рода [b1,a1]=cheby2(9,35,4/14); % определение параметров фильтра % Чебышева второго рода Fs=100; % частота диcкретизации [H,w] = freqz(b,a,512); % определение АЧХ фильтра [H1,w] = freqz(b1,a1,512); % определение АЧХ фильтра plot(w*Fs/(2*pi),abs(H), w*Fs/(2*pi),abs(H1)), grid; % вывод графика АЧХ xlabel('Частота (Гц)'); % подпись оси Х («Частота») ylabel('Амплитуда'); % подпись оси Y («Амплитуда») legend({'АЧХ фильтра Чебышева 1 рода','АЧХ фильтра Чебышева 2 рода'});

Программа для определения спектральных плотностей составляющих сигнала:

sf=filter(b,a,s); %фильтрация сигнала S = fft(s,512); %БПФ сложного сигнала SF = fft(sf,512); %БПФ отфильтрованного сигнала w = (0:255)/256*(Fs/2); % разбиение частотной оси на 256 значений plot(w,abs([S(1:256)' SF(1:256)'])); grid; % построение графика АЧХ xlabel('Frequency (Hz)'); % подпись оси Х («Частота, Гц») ylabel('Mag. of Fourier transform'); % подпись оси Y («Значение преобразования Фурье») legend({'input signal','filtered signal'});% подпись графиков («Входной сигнал, Фильтрованный сигнал»)

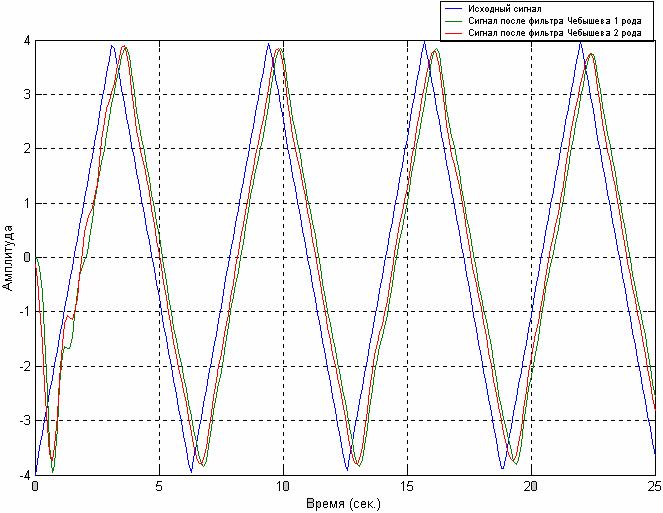
Программа фильтрации сигнала:

[b,a]=cheby1(6,0.06,4/14); %определение параметров фильтра % Чебышева первого рода [b1,a1]=cheby2(9,35,4/14); % определение параметров фильтра % Чебышева второго рода sf=filter(b,a,s); %фильтрация сигнала фильтром №1 sf1=filter(b1,a1,s); %фильтрация сигнала фильтром №2 plot (t,x,t,sf), grid; %построение графика отфильтрованных % и требуемого сигналов legend ('Исходный сигнал','Сигнал после фильтра Чебышева 1 рода', 'Сигнал после фильтра Чебышева 2 рода ',4); % подпись графиков сигналов

ВЫВОДЫ

Аппроксимация сигнала производилась полиномами Чебышева первого (пульсации в полосе пропускания) и второго (пульсации в полосе задерживания) рода, первый из которых имел неравномерность АЧХ в полосе пропускания. Фильтр Чебышева второго рода обладал меньшей шириной полосы, нежели фильтр первого рода и имел неравномерность АЧХ в полосе задерживания, но при этом обеспечивал большую крутизну затухания. Следовательно, фильтр Чебышева 1 рода необходимо использовать, когда требуется большая скорость затухания вне полосы пропускания и не предъявляются требования по обеспечению минимальных искажений АЧХ в полосе пропускания. Фильтр второго рода следует применять при повышенных требованиях к искажению при фильтрации.

На основе рассчитанных коэффициентов b,a построена спектральная плотность сложного входного и выходного фильтрованного сигнала. На графике отчетливо заметно, что после прохождения через фильтр синусоидальная и шумовая составляющая подавлены. Задержка выходного сигнала объясняется началом фильтрации только после накопления предшествующих n+1 значений, где n-порядок фильтра.

ЗАДАНИЕ