Примеры

1. Разложить в ряд Фурье на отрезке функцию

>>Решение <<

2. Разложить в ряд Фурье на интервале функцию .

>>Решение<<

6. Разложение функции, заданной на отрезке, в ряд по синусам или косинусам

Пусть ограниченная кусочно-монотонная функция задана на отрезке . Значения этой функции на отрезке можно доопределить различным образом. Например, можно определить функцию на отрезке так, чтобы . В этом случае говорят, что «продолжена на отрезок четным образом»; ее ряд Фурье будет содержать только косинусы. Если же функцию определить на отрезке так, чтобы , то получится нечетная функция, и тогда говорят, что «продолжена на отрезок нечетным образом»; в этом случае ее ряд Фурье будет содержать только синусы.

Итак, каждую ограниченную кусочно-монотонную функцию , определенную на отрезке , можно разложить в ряд Фурье и по синусам, и по косинусам.

Примеры

1. Функцию разложить в ряд Фурье: а) по косинусам; б) по синусам.

>>> решение <<<

7. Ряд Фурье для функции с произвольным периодом

Пусть функция является периодической с периодом . Для разложения её в ряд Фурье на отрезке , сделаем замену переменной, положив 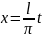. Тогда функция будет периодической функцией аргумента t с периодом 2π, т.к.

и ей можно разложить на отрезке в ряд Фурье

где

Возвращаясь к переменной x, т.е. положив , получим

Все теоремы, справедливые для рядов Фурье периодических функций с периодом 2π, остаются в силе и для периодических функций с произвольным периодом . В частности, сохраняет свою силу и достаточный признак разложимости функции в ряд Фурье.

Примеры

1. Разложить в ряд Фурье периодическую функцию с периодом , заданную на отрезке формулой

>>Решение и рисунок<<

Теорема №5

Если функция имеет период и интегрируема, то для любого числа a выполняется равенство

т.е. интеграл по отрезку, длина которого равная периоду T, имеет одно и то же значение независимо от положения этого отрезка на числовой оси.

Доказательство

В самом деле,

Делаем замену переменной во втором интеграле, полагая Это дает

и следовательно,

Что и требовалось доказать.

Г

рис. 10

еометрически это свойство означает, что в случае площади заштрихованных на рис.10 областей равны между собой.

Примеры

2. Функция является периодической с периодом В силу нечетности данной функции без вычисления интегралов можно утверждать, что при любом a

>>> тут еще замечание должно быть <<<

3. Разложить в ряд Фурье заданную на интервале функцию

с периодом 2π.

>> решение <<

8. Комплексная запись ряда Фурье

П

(1)

усть функция удовлетворяет достаточным условиям разложимости в ряд Фурье. Тогда на отрезке её можно представить рядом вида

Используя формулы Эйлера

найдем, что

П

(2)

одставляя эти выражения в ряд (1) вместо и , будем иметь

Введем следующие обозначения

Тогда ряд (2) примет вид

Преобразуем правую часть этого равенства следующим образом

П

(3)

оследнее равенство можно записать так:

Таким образом, ряд Фурье (1) представлен в комплексной форме (3).

Найдем выражения коэффициентов и 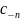через интегрирование. Имеем

Аналогично находим

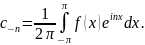
Окончательно формулы для и и можно записать так:

Коэффициенты называются комплексными коэффициентами Фурье функции .

Д

(4)

ля периодической функции с периодом комплексная форма ряда Фурье примет вид

где коэффициенты вычисляются по формулам

Сходимость рядов (3) и (4) понимается так: эти ряды называются сходящимися для данного значения x , если существуют пределы

Примеры

1. Разложить в комплексный ряд Фурье функцию периода 2π

…. решение….

9. Ряд Фурье

по общим ортогональным системам функций

9.1. Ортогональные системы функций

Обозначим через 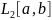множество всех действительных функций, определенных и интегрируемых на отрезке с квадратом, т.е. таких, для которых существует интеграл

В частности, все функции , непрерывные на отрезке , принадлежат , и значения их интегралов Лебега совпадают со значениями интегралов Римана.

С

(1)

истема функций , где , называется ортогональной на отрезке , если

(имеется ввиду интеграл Лебега)

Замечание. Условие (1) предполагает, в частности, что ни одна из функций не равна тождественно нулю.

Введем обозначение

и назовем величину нормой функции .

Если в ортогональной системе для всякого n имеем , то система функций называется ортонормированной.

Если система ортогональна, то система 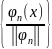ортонормирована.