2.2.4 Расчет червячной передачи
Число заходов червяка Z1=4.
Z2=Z1·U (3.6)
Z2=50 – число зубьев колеса.
Коэффициент диаметра червяка
qопт=0,25·Z2 (3.7)
qопт =0,25·50=12,5
Назначаем из стандартного ряда ГОСТ 19672-74 q=12,5.
Межосевое расстояние червячной передачи определяем по формуле
(3.8)
где K – коэффициент нагрузки;
q1 – коэффициент смещения червяка.
При проектном расчете коэффициент нагрузки принимают равным
0,5(Kβ
+1),
(3.9)
где Kβ – начальный коэффициент концентрации нагрузки.
Тогда
0,5(1,18+1)=1,09.
Из
нормального ряда чисел и конструктивных
соображений принимаем.
Модуль передачи определяется по формуле
m=2aw/(Z2+q) (3.10)
m= 10мм.
Согласуем со стандартным рядом ГОСТ 2144-76 m=10 мм.
Для сохранения стандартного межосевого расстояния определяем коэффициент смещения
x=aw/m-0,5(q+Z2), (3.11)
x=0.
Червяк:
Делительный диаметр d1=m·q (3.12)
d1=12,5·10=125 мм.
Диаметр вершин витков da1=d1+2m (3.13)
da1=145мм.
Диаметр впадин df1=d1-2,4m (3.14)
df1=125-2,4·10=101 мм
Длина
нарезной части червяка
b1
(10+5,5[x]+Z1)m (3.15)
b1 (10+4)·12.5=175 мм.
Для шлифуемых червяков длину увеличивают на 25 мм. Принимаем b1=200 мм.
Угол
подъема линий витков червяка
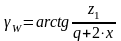(3.16)
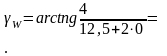17,74472
֠
Червячное колесо:
Делительный диаметр d2= m·Z2
d2= 10·50=500 мм.
Диаметр вершин зубьев в среднем сечении da2= d2+2m(1+x) (3.17)
da2=500+2·10(1+0)=520 мм.
Наибольший диаметр колеса dam2 da2+6m/(Z1+2) (3.19)
dam2 520+6·10/(4+2)= 530 мм.
Ширина колеса b2=ψa aw = 0,355·312,5 = 110 мм (3.20)
Скорость скольжения:
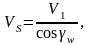(3.21)
где V1 – окружная скорость червяка, м/с.
(3.22)
Тогда
,
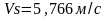Коэффициент полезного действия червячной передачи
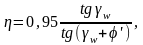(3.23)
где φ’ – приведенный угол трения.
Тогда
.
2.2.5. Проверочный расчёт передачи на контактную прочность.
Осуществляется по формуле
, (3.24)
где K – коэффициент нагрузки,
К=Кβ·КV , (3.25)
где Кβ – коэффициент концентрации нагрузки;
КV – коэффициент динамической нагрузки, при постоянной нагрузке.
Kβ=1+(z2/θ)3(1-x) , (3.26)
Kβ=1+(50/100)3(1-0)=1,08.
Где
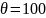- коэффициент деформации червяка
Определяем окружную скорость колеса
(3.27)
.
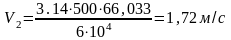Назначаем КV=1.
Тогда К=1·1,08=1,08
.
.
Условие контактной прочности
выполняется.
2.2.6. Проверка зубьев колеса на напряжения изгиба.
Формула условия прочности на изгиб имеет вид
,
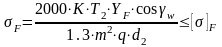где YF – коэффициент формы зуба, который принимают в зависимости от эквивалентного числа зубьев колеса ZV2.
ZV2=Z2/cos3γw (3.28)
ZV2=50/cos317,74=58.
Назначаем YF = 1,64.
,
σF=19,716 МПа < =90,9 МПа.
Прочность зубьев на изгиб обеспечена.
2.2.7. Определение усилий в зацеплении
Окружная сила на колесе, равная осевой силе на червяке
Ft2=Fa1=2T2/d2 (3.29)
Ft2=Fa1=16,287 кН.
Окружная сила на червяке, равная осевой силе на колесе
Fa2= Ft1=2T1/d1 (3.30)
Fa2= Ft1=2·411,3/125=6,58 кН.
Радиальная сила Fr= Ft2·tgαx , (3.31)
где αx =20˚ - угол зацепления.
Тогда
Fr=5,927кН.