12. Алгебраическая величина момента пары сил.

Алгебраической величиной момента пары сил называют взятое с определенным знаком произведение модуля одной из сил, составляющих пару, на плечо пары сил:

.

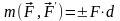Знак плюс берется, если пара стремиться повернуть тело против часовой стрелки и минус – если по часовой (рисунки 2.11 а и б).

,

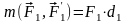Так как момент пары полностью характеризует действие пары, то иногда пару сил изображают в виде дуговой стрелки с указанием ее момента 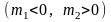(рисунок 1.11 в).

12. Главный вектор и главный момент произвольной плоской системы сил.

Для произвольной плоской системы сил главный вектор является геометрической суммой всех сил и проектируется на две оси декартовой системы координат.

.

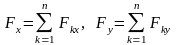Величина (модуль) главного вектора определяется по формуле:

,

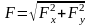а направление – с помощью направляющих косинусов:

, .

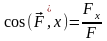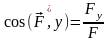Главный момент относительно точки О в этом случае является алгебраической суммой моментов всех сил относительно точки О:

.

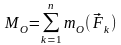Если на тело кроме сил действуют пары, то их моменты добавляются в главный момент системы.

12. Аналитические условия равновесия произвольной плоской системы сил (три формы).

Из общих условий равновесия системы сил вытекают векторные условия равновесия произвольной плоской системы сил:

,

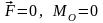которые в аналитической форме записываются в виде скалярных условий равновесия в первой форме.

Первая форма условий равновесия произвольной плоской системы сил: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на две координатные оси (х и у), лежащие в плоскости действия сил, и алгебраическая сумма моментов всех сил относительно любой точки О были равны нулю:

.

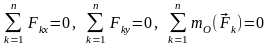Кроме этого можно аналитические условия равновесия произвольной плоской системы сил записать еще в двух формах.

Вторая форма условий равновесия произвольной плоской системы сил: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций всех сил на ось (х), лежащую в плоскости действия сил, и алгебраические суммы моментов всех сил относительно двух точек (А и В), не лежащих на одном перпендикуляре к этой оси, были равны нулю:

.

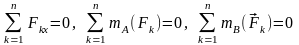Третья форма условий равновесия произвольной плоской системы сил: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно трех точек (А, В и С), не лежащих на одной прямой, были равны нулю:

.

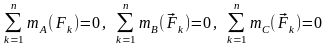При решении задач, в тех случаях, когда сложно определить плечо силы относительно точки, можно силу разложить на составляющие и воспользоваться теоремой Вариньона.

12. Распределенные силы и определение их равнодействующей.

13. Реакция жесткой заделки.

14. Условия равновесия системы тел.

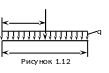Силы, приложенные в одной точке тела, называются сосредоточенными силами. Кроме таких сил, существуют силы, действующие вдоль отрезка, плоскости или в объеме. Такие силы называются распределенными. Для произвольной плоской системы сил будем рассматривать силы, распределенные вдоль отрезка прямой. Равномерно распределенной силой (нагрузкой) называется сила, действие которой равномерно распределено вдоль отрезка прямой (рисунок 1.12). При этом задается интенсивность распределения этой силы (q), то есть сила, приходящаяся на единицу длины нагруженного отрезка. В этом случае равномерно распределенная сила заменяется равнодействующей 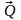, модуль которой

,

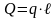а приложена она в середине отрезка (рисунок 1.12).

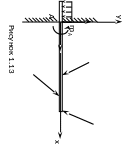
Неподвижной защемляющей опорой (жесткой заделкой) называется связь, осуществляемая в виде заделки консольной балки в жесткую конструкцию. В этом случае на балку в ее поперечном сечении действует со стороны заделанного конца система распределенных сил (реакций).

Считая эти силы приведенными к центру А сечения, можно их заменить одной силой, имеющей составляющие и , приложенные в этом центре, и парой с моментом 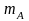(рисунок 1.13).

При рассмотрении равновесия системы тел (составной конструкции), связанных между собой, необходимо систему разбить на отдельные тела и исследовать равновесие каждого из тел отдельно, добавляя силы реакций (внутренние силы) со стороны отделенных тел. При этом, согласно четвертой аксиоме, силы реакций, с которыми разделенные тела действуют друг на друга, равны по величине и противоположны по направлению.