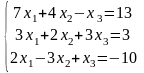- •1.2. Действия над матрицами
- •§ 2. Определители
- •2.1. Определители 2-го и 3-го порядка
- •2.2. Минор и алгебраическое дополнение
- •§ 3. Невырожденные матрицы
- •3.1. Обратная матрица
- •§ 4. Системы линейных уравнений
- •4.1. Виды систем линейных уравнений
- •4.2. Матричная запись систем линейных уравнений
- •4.3. Решение систем линейных уравнений матричным методом
- •4.4. Решение систем линейных уравнений методом Крамера
- •Контрольная работа №1
- •1. Даны две матрицы а и в Найти: а) ав; б) ва; в) а-1; г) аа-1; д) а-1а; е) в-1; ж) определитель матрицы а; з) определитель матрицы в.
- •2. Проверить совместность системы и в случае совместности решить ее:
4.3. Решение систем линейных уравнений матричным методом
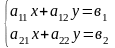 ,
А=
-
основная матрица; В=
,
А=
-
основная матрица; В= -
матрица столбец свободных членов; Х=
-
матрица столбец свободных членов; Х=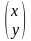 -
матрица столбец неизвестных.
-
матрица столбец неизвестных.
Х= А-1В [1.14]- формула для решения систем линейных уравнений матричным методом.
Пример
1)
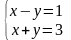 ,
А=
,
А=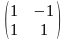 ,
В=
,
В=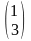 ,
Х=
,
А-1=
,
Х=
,
А-1=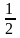
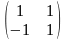 ;
;
применим формулу: Х= А-1В=
=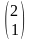 ,
значит х=2, у=1.
,
значит х=2, у=1.
2)
 ,
А=
,
В=
,
А=
,
В=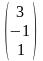 ,
Х=
,
Х=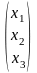 ,
А-1=-
;
,
А-1=-
;
применим формулу: Х= А-1В=-
= ,
значит х1=2, х2=0, х3=-1.
,
значит х1=2, х2=0, х3=-1.
4.4. Решение систем линейных уравнений методом Крамера
Для решения система n
линейных уравнений с n
неизвестными применяются формулы: х1=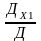 ,
х2=
,
х2=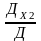 ,
…, хn=
,
…, хn=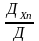 [1.15]; где х1, х2, …, хn-
неизвестные, Д- определитель основной
матрицы; ДХ1- определитель основной
матрицы в котором первый столбец заменили
столбцом свободных членов, ДХ2-
определитель основной матрицы в котором
второй столбец заменили столбцом
свободных членов, …., ДХn-
определитель основной матрицы в котором
n-ый столбец заменили
столбцом свободных членов.
[1.15]; где х1, х2, …, хn-
неизвестные, Д- определитель основной
матрицы; ДХ1- определитель основной
матрицы в котором первый столбец заменили
столбцом свободных членов, ДХ2-
определитель основной матрицы в котором
второй столбец заменили столбцом
свободных членов, …., ДХn-
определитель основной матрицы в котором
n-ый столбец заменили
столбцом свободных членов.
Частные случаи
1) Пусть Д≠0, ДХ1≠0, ДХ2≠0, …, ДХn≠0- тогда система имеет единственное решение.
2) Пусть Д=0, ДХ1≠0, ДХ2≠0, …, ДХn≠0- тогда система не имеет решений.
3) Пусть Д=0, ДХ1=0, ДХ2=0, …, ДХn=0- тогда система имеет бесконечное множество решений (см. метод Гаусса).
Однородная система линейных уравнений
1) Пусть Д≠0, ДХ1=0, ДХ2=0, …, ДХn=0- тогда система имеет единственное решение (х1=х2=…=хn=0).
2) Пусть Д=0, ДХ1=0, ДХ1=0, …, ДХn=0- тогда система имеет бесконечное множество решений (см. метод Гаусса).
Пример
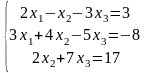 ,
Д=
,
Д=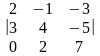 =79,
ДХ1=
=79,
ДХ1=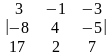 =395,
ДХ2=
=395,
ДХ2= =-158,
ДХ3=
=-158,
ДХ3=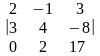 =237,
х1=
=5,
х2=
=-2,
х3=
=237,
х1=
=5,
х2=
=-2,
х3= =3.
=3.
Контрольная работа №1
Линейная алгебра
1. Даны две матрицы а и в Найти: а) ав; б) ва; в) а-1; г) аа-1; д) а-1а; е) в-1; ж) определитель матрицы а; з) определитель матрицы в.
1) А=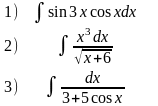 ,
В=
,
В=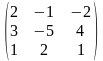
2) А=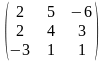 ,
В=
,
В=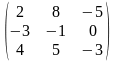
3) А=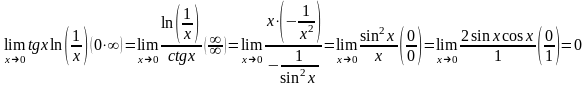 ,
В=
,
В=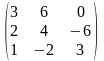
4) А=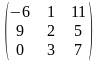 ,
В=
,
В=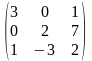
5) А= ,
В=
,
В=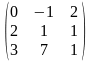
6) А=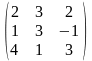 ,
В=
,
В=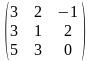
7) А= ,
В=
,
В=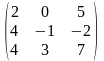
8) А= ,
В=
,
В=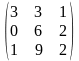
9) А=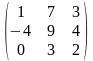 ,
В=
,
В=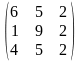
10) А=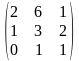 ,
В=
,
В=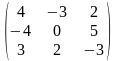
11) А=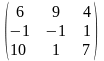 ,
В=
,
В=
12) А=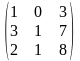 ,
В=
,
В=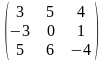
13) А=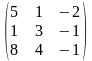 ,
В=
,
В=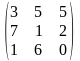
14) А=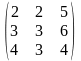 ,
В=
,
В=
15) А=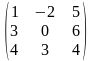 ,
В=
,
В=
16)
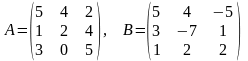
17)

18)

19)

20)

21)
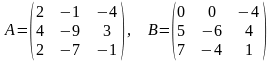
22)
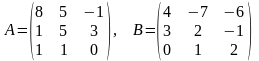
23)
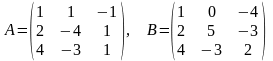
24)
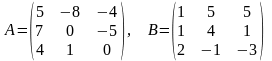
25)

26)
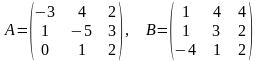
27)
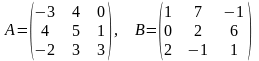
28)
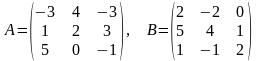
29)

30)
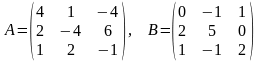
2. Проверить совместность системы и в случае совместности решить ее:
а) по формулам Крамера;
b) матричным методом.
1)
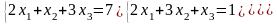
2)
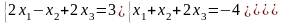
3)

4)
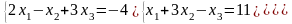
5)
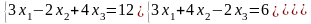
6)
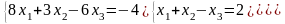
7)

8)

9)
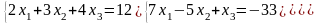
10)
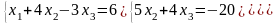
11)
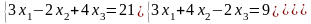
12)
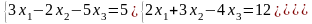
13)

14)
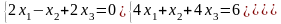
15)
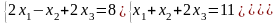
16)
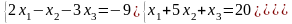
17)
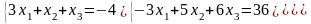
18)
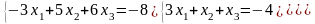
19)
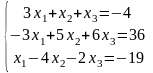
20)
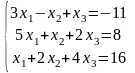
21)
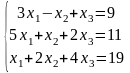
22)
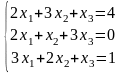
23)
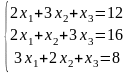
24)
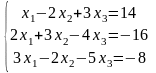
25)
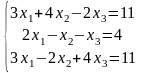
26)
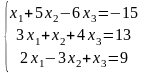
27)

28)
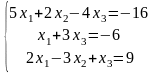
29)
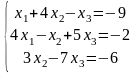
30)