
- •1.2. Действия над матрицами
- •§ 2. Определители
- •2.1. Определители 2-го и 3-го порядка
- •2.2. Минор и алгебраическое дополнение
- •§ 3. Невырожденные матрицы
- •3.1. Обратная матрица
- •§ 4. Системы линейных уравнений
- •4.1. Виды систем линейных уравнений
- •4.2. Матричная запись систем линейных уравнений
- •4.3. Решение систем линейных уравнений матричным методом
- •4.4. Решение систем линейных уравнений методом Крамера
- •Контрольная работа №1
- •1. Даны две матрицы а и в Найти: а) ав; б) ва; в) а-1; г) аа-1; д) а-1а; е) в-1; ж) определитель матрицы а; з) определитель матрицы в.
- •2. Проверить совместность системы и в случае совместности решить ее:
Всё что выделено красным, это для самост.изучения
Глава I. Линейная алгебра
§1. Матрицы
1.1. Матрицы. Виды матриц.
Матрицей называется упорядоченная таблица чисел, состоящая из m строк и n столбцов.
Число строк и столбцов (m n)
называется размером матрицы.
n)
называется размером матрицы.
аij называется элементом матрицы, где i-номер строки, j-номер столбца матрицы.
Пример
а) А=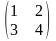 размер
матрицы 2
2,
а11=1, а21=3.
размер
матрицы 2
2,
а11=1, а21=3.
б) В= размер
матрицы 4
3,
а33=13, а41=4, а12=0.
размер
матрицы 4
3,
а33=13, а41=4, а12=0.
Виды матриц
Матрица называется квадратной, если в ней число строк равно числу столбцов.
Если в матрице число строк не равно числу столбцов, то такая матрица называется прямоугольной.
Пример
А=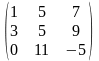 -квадратная
матрица; В=
-квадратная
матрица; В=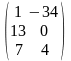 -прямоугольная
матрица.
-прямоугольная
матрица.
Матрица, элементы которой составляют строку, называется матрица строка.
Матрица, элементы которой составляют столбец, называется матрица столбец.
Пример А=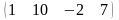 -
матрица строка; В=
-
матрица строка; В= -
матрица столбец.
-
матрица столбец.
Главная диагональ квадратной матрицы- это диагональ, которая начинается с элемента а11.
Квадратная матрица, у которой на главной диагонали единицы, а все остальные элементы равны нулю, называется единичной матрицей.
Матрица, у которой все элементы равны нулю, называется нулевой матрицей.
Пример
Е=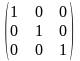 -
единичная матрица; О=
-
единичная матрица; О= -
нулевая матрица.
-
нулевая матрица.
Матрица, в которой строки и столбцы заменены местами, называется транспонированной матрицей Ат.
Пример
Если А=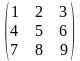 ,
тогда Ат=
,
тогда Ат= .
.
1.2. Действия над матрицами
1. Равенство матриц.
Две матрицы называются равными, если они одного размера и равны их соответствующие элементы.
Пусть А= ,
В=
,
В= ,
тогда А=В, если аij=вij.
,
тогда А=В, если аij=вij.
2. Сложение матриц.
При сложении матриц (одного размера) складываются их соответствующие элементы.
Пусть А=
,
В=
,
А+В=С, С=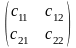 ,
где сij= аij+вij. [1.1]
,
где сij= аij+вij. [1.1]
Пример
А=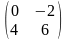 ,
В=
,
В=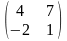 ,
А+В=
,
А+В= .
.
Свойства сложения матриц.
А+В=В+А
(А+В)+С=А+(В+С)
А+О=О+А=А
3. Умножение матрицы на число.
При умножение матрицы на число, каждый элемент матрицы умножается на это число.
Пусть А=
,
λ≠0, λ=conct, то λА=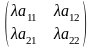 [1.2].
[1.2].
Пример
А=
,
λ=3, λА=
Свойства умножения матриц на число.
λ,β≠0, λ,β=conct λ(А+В)= λА+ λВ
(λ+ β)А= λА+βА
λ(βА)=λβА
4.Умножение матриц.
1) Квадратные матрицы (одного размера)
Пусть А= , В= , АВ=С С= , где с11=а11в11+а12в21; с12=а11в12+а12в22; с21=а21в11+а22в21; с22=а21в12+а22в22 [1.3].
Пример
а)
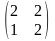
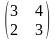 =
=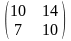 б)
б)

 =
= .
.
2) Прямоугольные матрицы.
Прямоугольные матрицы можно перемножать тогда, когда число столбцов первой матрицы равно числу строк второй матрицы. В результате получится новая матрица, в которой столько строк, сколько строк в первой и столько столбцов, сколько столбцов во второй.

Пример
а)
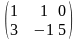
 =
=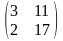 ,
3 столбца=3 строкам, (2
2)-новая
матрица;
,
3 столбца=3 строкам, (2
2)-новая
матрица;
б)
= ,
2 столбца=2 строкам, (3
3)-новая
матрица;
,
2 столбца=2 строкам, (3
3)-новая
матрица;
в)
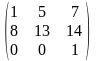
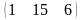 ,
3 столбца≠1 строке- перемножать матрицы
нельзя.
,
3 столбца≠1 строке- перемножать матрицы
нельзя.
Свойства умножения матриц.
АВ≠ВА
(АВ)С=А(ВС)
АЕ=ЕА=А
§ 2. Определители
2.1. Определители 2-го и 3-го порядка
Для квадратных матриц существует числовая характеристика, называемая определителем (обозначение: Д или det).
Вычисление определителей второго порядка (2 2)
 =а11а22-а21а12
[1.4];
=а11а22-а21а12
[1.4];
Пример
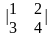 =1∙4-3∙2=-2.
=1∙4-3∙2=-2.
Вычисление определителей третьего порядка (3 3)
Перемножим элементы, расположенные на главной диагонали и прибавим к ним произведение элементов, расположенных в вершинах треугольников. Затем вычтем произведение элементов, расположенных на побочной диагонали и произведение элементов в вершинах треугольников.

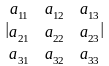 =а11а22а33+а21а32а13+а12а23а31-а31а22а13-а32а23а11-а21а12а33
[1.5].
=а11а22а33+а21а32а13+а12а23а31-а31а22а13-а32а23а11-а21а12а33
[1.5].
Пример
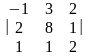 =-1∙8∙2+2∙1∙2+3∙1∙1-1∙8∙2-1∙1∙(-1)-2∙3∙2=-16+4+3-16+1-12=-36
=-1∙8∙2+2∙1∙2+3∙1∙1-1∙8∙2-1∙1∙(-1)-2∙3∙2=-16+4+3-16+1-12=-36
Свойства определителей
1) Значение определителя не
изменится при замене всех строк
соответствующими столбцами и наоборот:
=а11а22-а21а12;
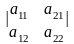 =
а11а22-а21а12.
=
а11а22-а21а12.
Пример
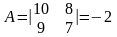
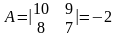
2) Если поменять местами две строки или два столбца определителя, то он изменит знак на противоположный: =а11а22-а21а12;
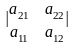 =
а21а12-
а11а22=-
а11а22-а21а12.
=
а21а12-
а11а22=-
а11а22-а21а12.
Пример


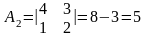
3) Определитель с двумя равными строками или столбцами равен нулю.
 =а11а12-
а11а12=0.
=а11а12-
а11а12=0.
4) Если умножить элементы,
какой- либо строки или столбца на λ≠0,
λ=conct,
то определитель увеличится в λ раз:
 =
λа11а22-
λа21а12=
λ(а11а22-а21а12).
=
λа11а22-
λа21а12=
λ(а11а22-а21а12).
Пример


5) Если все элементы строки
или столбца определителя равны нулю,
то весь определитель равен нулю:
 =
а110-
а210=0.
=
а110-
а210=0.
6) Определитель не изменится, если прибавить к элементам некоторой строки (столбца) элементы другой строки (столбца) умноженные на λ≠0, λ=conct:
=а11а22-а21а12,
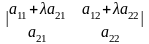 =а22(а11+
λа21)-а21(а12+
λа22)=
а22а11+
а22
λа21-
а21
а12-
=а22(а11+
λа21)-а21(а12+
λа22)=
а22а11+
а22
λа21-
а21
а12-
-а21 λа22= а11а22-а21а12.
Пример
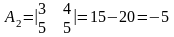
 (к 2 строке + 1 строку)
(к 2 строке + 1 строку)
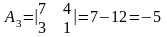 (к 1 столбцу + 2 столбец)
(к 1 столбцу + 2 столбец)
