6.2. Решение типовых задач.

Пример 1. По данным за 18 месяцев построено уравнение регрессии зависимости прибыли предприятия y (млн. руб.) от цен на сырье x₁ (тыс. руб. за 1т) и производительности труда x₂ (ед. продукции на 1 работника):

.

При анализе остаточных величин были использованы значения, приведенные в табл. 6.1:

Таблица 6.1

№	y	x1	x2
1	210	800	300
2	720	1000	500
3	300	1500	600
	…	…	…

.

Требуется:

1. По трем позициям рассчитать , , , , .

2. Рассчитать критерий Дарбина – Уотсона.

3. Оценить полученный результат при 5%-ном уровне значимости.

4. Указать, пригодно ли уравнение для прогноза.

Решение:

1. определяется путем подстановки фактических значений x₁ и x₂ в уравнение регрессии: ;

;

.

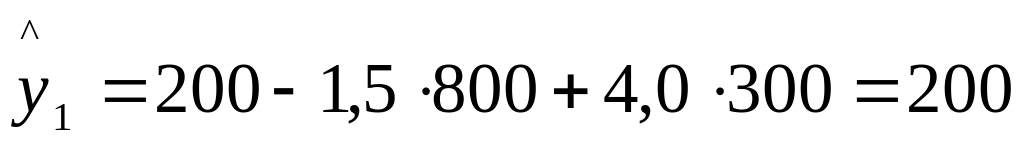Остатки _t рассчитываются по формуле . Следовательно, , , ; , , ;

- те же значения, что и _t , но со сдвигом на один месяц.

Результаты вычислений оформим в виде табл. 6.2:

Таблица 6.2

№
1	200	10	-	-	-	100
2	700	20	10	10	100	400
3	350	-50	20	-70	4900	2500
…	…	…	…	…	…	…
					40000	10500

2. Критерий Дарбина – Уотсона рассчитывается по формуле

.

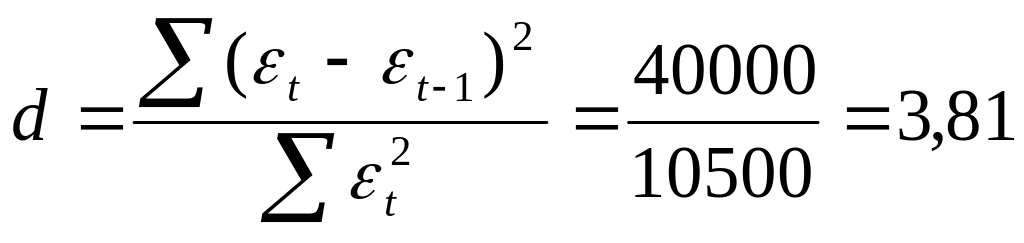3. Фактическое значение d сравниваем с табличными значениями при 5%-ном уровне значимости. При n=18 месяцев и m=2 (число факторов) нижнее значение d равно 1,05, а верхнее – 1,53. Так как фактическое значение d близко к 4, можно считать, что автокорреляция в остатках характеризуется отрицательной величиной. Чтобы проверить значимость отрицательного коэффициента автокорреляции, найдем величину 4–d=4–3,81=0,19, что значительно меньше, чем d. Это означает наличие в остатках автокорреляции.

4. Уравнение регрессии не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор. Возможно также, что форма связи неточна, а может быть, в рядах динамики имеется общая тенденция.

6.3. Реализация типовых задач на компьютере.

Решение с помощью ППП Excel

1. Для определения параметров линейного тренда по методу наименьших квадратов используется статистическая функция ЛИНЕЙН, для определения экспоненциального тренда – ЛГРФПРИБЛ. Порядок вычисления был рассмотрен в главе пункт 2.3. В качестве зависимой переменной в данном примере выступает время (t=1,2,…, n). Введем исходные данные и выполним вычисления с помощью функций ЛИНЕЙН и ЛГРФПРИБЛ:

А	В	С
1	Год, х	Выпуск продукции, у
2	1961	1054
3	1962	1104
4	1963	1149
5	1964	1291
6	1965	1427
7	1966	1505
8	1967	1513
9	1968	1635
10	1969	1987
11	1970	2306
12	1971	2367
13	1972	2913
14	1973	3837
15	1974	5490
16	1975	5502
17	1976	6342
18	1977	7665
19	1978	8570
20	1979	11172
21	1980	14150
22	1981	14004
23	1982	13088
24	1983	12518
25	1984	13471
26	1985	13617
27	1986	16356
28	1987	20037
29	1988	21748
30	1989	23298
31	1990	26570
32	1991	23080
33	1992	23981
34	1993	23446
35	1994	29658
36	1995	39573
37	1996	38435

Запишем уравнение линейного и экспоненциального тренда, используя полученные результаты:

,

.

2. Построение графиков осуществляется с помощью Мастера диаграмм.

Порядок построения следующий:

1. введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2. активизируйте Мастер диаграмм любым из следующих способов:

   1. в главном меню выберите Вставка/Диаграмма;

   2. на панели инструментов Стандартная щелкните по кнопке Мастер диаграмм;

3. в окне Тип выберите График; вид графика выберите в поле рядом со списком типов. Щелкните по кнопке Далее;

4. заполните диапазон данных. Установите флажок размещения данных в строках. Щелкните по кнопке Далее;

5. заполните параметры диаграммы на разных закладках: названия диаграммы и осей, значения осей, линии сетки, параметры легенды, таблица и подписи данных. Щелкните по кнопке Далее;

6. укажите место размещения диаграммы на отдельном или на имеющемся листе. Щелкните по кнопке Далее, а затем по кнопке Готово.

В ППП MS Excel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:

1. выделите область построения диаграммы, а затем в главном меню выберите Диаграмма / Добавить линию тренда;

2. в появившемся диалоговом окне выберите вид линии тренда и задайте соответствующие параметры. Для полиномиального тренда необходимо задать степень аппроксимирующего полинома, для скользящего среднего – количество точек усреднения.

В качестве дополнительной информации на диаграмме можно отобразить уравнение регрессии и значение среднеквадратического отклонения, установив соответствующие флажки на закладке Параметры. Щелкните по кнопке ОК.

3. Сравним значения R² по разным уравнениям трендов:

   • полиномиальный 6-й степени – R²=0,9728;

   • экспоненциальный – R²=0,9647;

   • линейный – R²=0,8841;

   • степенной – R²=0,8470;

   • логарифмический – R²=0,5886.

Исходные данные лучше всего описывает полином 6-й степени. Следовательно, в рассматриваемом примере для расчета прогнозных значений следует использовать полиномиальное уравнение.