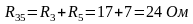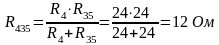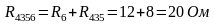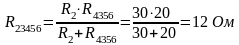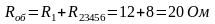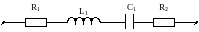Примеры решения задач Пример 1.

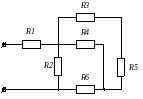
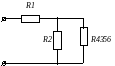
В цепи постоянного тока со смешанным соединением резисторов определить токи, напряжения и мощности каждого участка, составить уравнение баланса мощностей. Ответить на вопрос: как изменится величина напряжения U₆, если один из резисторов замкнуть накоротко?

Дано: U = 100 В R1 = 8 Ом R2 = 30 Ом R3 = 17 Ом R4 = 24 Ом R5 = 7 Ом R6 = 8 Ом R4 замкнут накоротко

Решение :

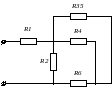
	Резисторы R3 и R5 соединены последовательно:
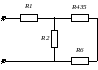
	Резисторы R35 и R4 соединены параллельно:
	Резисторы R6 и R435 соединены последовательно:
	Резисторы R2 и R4356 соединены параллельно:
	Резисторы R1 и R23456 соединены последовательно:

Разворачивая схему определяем все токи и напряжения на всех участках цепи:

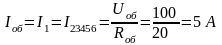
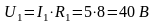
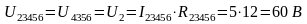
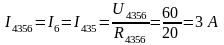
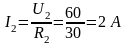
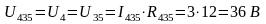
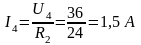
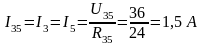
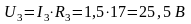
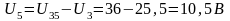
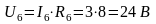
Правильность решения проверяем балансом мощностей.

Баланс мощностей:

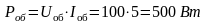
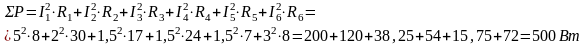
500 = 500

Пример 2

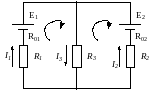
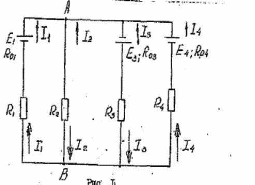
Определите токи ветвей электрической цепи, изображенной на рис-1, пользуясь методом узлового напряжения.

Дано: Е₁ = 70 В; Е₃ = 100 В; Е₄ = 200 В; R₀₁ = 2 Ом; R₀₃ = R₀₄ = 1 Ом;

R₁ = 18 Ом; R₂ = 5 Ом; R₃ = 24 Ом; R₄ = 9 Ом;

Решение.

I. Примем направление токов в ветвях к одному узлу - узлу А (рис. 1), тогда э.д.с. Е₁ и Е₄ считаются положительными, а э.д.с. Е₃ - отрицательной.

Узловое напряжение:

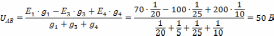
где

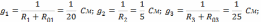
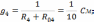
Токи ветвей

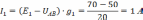
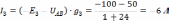
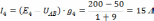
Знак «-» у тока означает, что его направление противоположно принятому предварительно. Действительные направления показаны на схеме двойными стрелками.

Пример 3

Определите токи ветвей цепи постоянного тока, применив метод узловых и контурных уравнений (по 1 и 2 законам Кирхгофа).

Составьте уравнение баланса мощностей.

Дано: Е1 = 100 В Е2 = 60 В R01 = 1 Ом R02 = 2 Ом R1 = 36 Ом R2 = 28 Ом R3 = 10 Ом

Решение :

В схеме 3 ветви и 2 узла, значит надо составить всего 3 уравнения, из них 1 – по первому закону (т.к. составляется (n-1)уравнение, где n – число узлов) и 2 по второму. Выбираем обходы контура – по часовой стрелке.

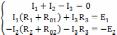
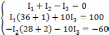
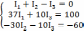
Решая систему уравнений, получим:

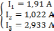
Составляем баланс мощностей:

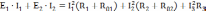
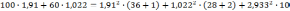
252,32 = 252,33

Баланс выполняется

Пример 4

Для неразветвленной цепи переменного тока определить следующие величины, если они не заданы: полное сопротивление, напряжение, приложенное к цепи, ток, угол сдвига фаз, активную, реактивную и полную мощности цепи. Частота тока f = 50 Гц.

Начертите в масштабе векторную диаграмму и поясните ее построение.

Поясните характер изменения тока, активной мощности и угла сдвига фаз в цепи при увеличении частоты в два раза.

R1 = 4 Ом R2 = 2 Ом L1 = 38,2 мГн

С1 = 796 мкФ Р= 24 Вт

Решение :

1). Сопротивления цепи:

а) индуктивное сопротивление: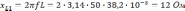

б) емкостное сопротивление:

в) полное сопротивление цепи:

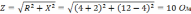
2). Ток, протекающий по цепи: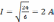

3). Напряжение, приложенное к цепи: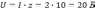

4). Мощности цепи:

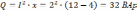
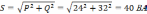
5). Угол сдвига фаз: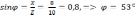

6). Для построения векторной диаграммы определяем падения напряжения на всех участках цепи:

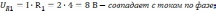
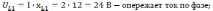
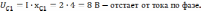
Масштаб: по току 0,25 А/см; по напряжению 2В/с.

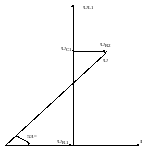
7). Если частоту увеличить в 2 раза, то:

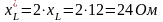
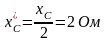
х = 24 - 2 = 12 Ом, → z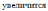 → I уменьшится → P уменьшится → φ останется положительным и увеличится (63°) по модулю