3. Коэффициент детерминации. Средняя ошибка аппроксимации.

Для оценки качества уравнения регрессии рассчитывают такие показатели, как:

1) Коэффициент детерминации показывает, какая часть вариации результата объяснена вариацией фактора:

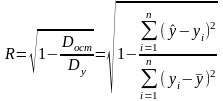(3)

или

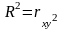
Коэффициент детерминации принимает значения в диапазоне 0 ≤ R ≤ 1.

Чем ближе к-т детерминации к 1, тем в большей степени уравнение пригодно для прогнозирования и тем лучше модель согласуется с данными наблюдений. При R=1 связь становится функциональной.

2) Средняя ошибка аппроксимации – показывает среднее отклонение расчетных значений от фактических:

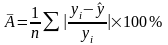(4)

Допустимый предел ошибки аппроксимации – не более 15%.

3) F-критерий Фишера и t-критерий Стьюдента, с помощью которых определяется надежность уравнения регрессии в целом и отдельно его параметров.

4. Проверка качества уравнения регрессии. F-критерий Фишера. T-критерий Стьюдента.

После того как уравнение регрессии найдено, проводится оценка значимости как уравнения в целом, так и его отдельных параметров.

Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. Согласно F-критерию Фишера, выдвигается «нулевая» гипотеза H₀ о статистической незначимости уравнения регрессии и показателя тесноты связи.

Непосредственному расчету F-критерия предшествует анализ дисперсии.

Наблюдаемые значения результативного признака yi можно представить в виде суммы двух составляющих ŷi и εi:

yi = ŷi+ εi

Из данного уравнения следует следующее соотношение между дисперсиями наблюдаемых значений переменной D(y), ее расчетных значений D(ŷ) и остатков D(е) (остаточной дисперсией Dост = D(ε)):

D(y) = D(ŷ) + D(ε)

= +

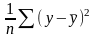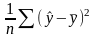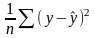
полная (общая) сумма квадратов отклонений

=

сумма квадратов отклонений, объясненная регрессией

+

(остаточная) сумма квадратов отклонений, не объясненная регрессией

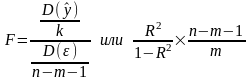
где m – число независимых переменных в уравнении регрессии (для парной регрессии m = 1);

n – число единиц совокупности.

Если нулевая гипотеза Н₀ справедлива, то факторная и остаточная дисперсии не отличаются друг от друга (т. е. отличие величины F от нуля статистически незначимо).

Если нулевая гипотеза Н₀ не справедлива, то факторная дисперсия превышает остаточную в несколько раз.

Справедливость (несправедливость) гипотезы Н₀ определяется по таблицам критических значений F-критерия Фишера, которые разработаны английским статистиком Снедекором для разных уровнях значимости нулевой гипотезы и различного числа степеней свободы.

Уровнем значимости (обозначается α) в статистических гипотезах называется вероятность отвергнуть верную гипотезу (это, так называемая, ошибка первого рода). Уровень значимости α обычно принимает значения 0,05 и 0,01, что соответствует вероятности совершения ошибки первого рода 5 % и 1 %.

Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. В таблице значений F-критерия Фишера число степеней свободы k1 = m, k2 = n -m-1.

Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном расхождении их для данного уровня вероятности наличия нулевой гипотезы.

Если Fфакт > Fтабл, то Н0 о случайной природе связи отклоняется и признается статистическая значимость и надежность уравнения.

Если Fфакт < Fтабл, то Н0 не отклоняется и признается статистическая незначимость уравнения регрессии.

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому параметру определяется его стандартная ошибка.

Стандартные ошибки параметров регрессии (ma, mb) определяются соотношениями:

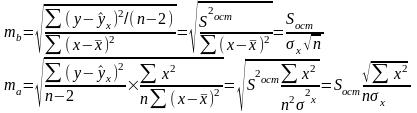
Сопоставляя оценки параметров и их стандартные ошибки можно сделать вывод о надежности (точности) полученных оценок.

Для оценки статистической значимости коэффициентов регрессии применяется t-критерий Стьюдента, согласно которому выдвигается «нулевая» гипотеза H0 о статистической незначимости коэффициента уравнения регрессии (т. е. о статистически незначимом отличии величины а или b от нуля):

Н₀: а=0, b=0

Эта гипотеза отвергается при выполнении условия t > tтабл, где tтабл определяется по таблицам t-критерия Стьюдента по числу степеней свободы k1 = n-m-1 (m - число независимых переменных в уравнении регрессии) и заданному уровню значимости α.

t-критерий Стьюдента используется и для оценки статистической значимости выборочного коэффициента корреляции rxy:

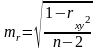
Оценка значимости параметров уравнения и коэффициента корреляции проводится путем сопоставления их значений с величиной случайной ошибки:

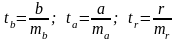
Если tфакт > tтабл, то Н0 отклоняется, т.е. a, b, r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х.

Если tфакт < tтабл, то Н0 не отклоняется и признается случайная природа формирования a, b, r.

Проверка значимости оценок параметров ничего не говорит о том, насколько эти оценки могут отличаться от точных значений. Ответ на этот вопрос дает построение доверительных интервалов.

Под доверительным интервалом понимаются пределы, в которых лежит точное значение определяемого показателя с заданной вероятностью (P = 1-α).

Доверительные интервалы для параметров a и b уравнения линейной регрессии определяются соотношениями:

;

;

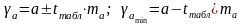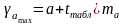
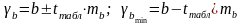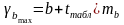
Если в границы доверительного интервала попадает ноль, т. е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается равным нулю, так как он не может одновременно принимать и положительное, и отрицательное значения.