Наземный гирокомпас(1г25-1).

Цель работы: ознакомление с принципом действия, конструкцией, режимами работы, тактико-техническими характеристи­ками прибора.

Назначение прибора: Гирокомпас 1Г25-1 предназначен для определения истинного азимута перпендикуляра к базовой оси установочного столика (обозначенной пазом и отверстием), при работе гирокомпаса на подвижном относительно Земли основании.

Состав лабораторной установки.

1. Гирокомпас.

2. Установочный столик.

3. Блок преобразования информации и управления.

4. Блок управления.

5. Блок питания.

6. Устройство амортизационно – фиксирующее.

7. Призма.

Порядок проведения лабораторной работы

1. Изучение теоретической части лабораторной работы, подготовка ответов на контрольные вопросы.

2. Ознакомление с устройством лабораторной установки.

3. Выполнение экспериментальной части.

4. Составление отчета.

Содержание отчета

1. Название и цель лабораторной работы.

2. Кинематическая схема с указанием приложенных к ГК моментов.

3. Алгоритм работы наземного ГК по рис.4

4. Экспериментальные данные.

1.Теоретическая часть

1. Принцип действия наземного гирокомпаса

Гирокомпас определяет истинный азимут ориентирного направления. В качестве ориентирного направления принято направление, перпендикулярное к контрольному элементу КЭ (рис.1). Контрольный элемент расположен на базовой оси установочного столика, на котором закреплен корпус гирокомпаса. Базовая ось обозначена пазом и отверстием. Азимут А отсчитывается от направления на север по часовой стрелке до нормали к КЭ.

Рис.1 Измеряемый азимут ориентирного направления.

Гирокомпас представляет собой гиромаятник, центр масс которого смещен относительно точки подвеса на величину (рис.2).

Чувствительный элемент (ЧЭ) гирокомпаса состоит из гиромотора 5 со штангой 4, подвешенного с помощью торсиона 2 в корпусе 6. Вращающийся ротор гиромотора, кинетический момент которого равен Н, имеет две степени свободы относительно корпуса (, ). Угол  характеризует угол отклонения оси Z в горизонтальной (азимутальной) плоскости от направления на север, угол  - угол отклонения оси Z от плоскости горизонта. На рис.2 показаны положительные направления отсчета углов , .

Для уменьшения вредных моментов, обуславливаемых закруткой торсиона на угол , верхний конец торсиона закреплен в кольце 1. С помощью следящей системы обеспечивается синхронное слежение кольца 1 за азимутальным движением ЧЭ. Движение ЧЭ по углу  фиксируется лимбом 3.

Рис.2 Кинематическая схема гирокомпаса.

Центр масс ЧЭ находится в точке О и смещен на величину вниз относительно точки подвеса О_п.

Направление на север совпадает с одной из осей географической системы координат , показанной на рис.3 для точки О земной поверхности.

Рис.3 Географическая системы координат.

Ось  направлена по истинной вертикали, ось  - по касательной к меридиану в сторону северного полюса N, ось  - по касательной к параллели в сторону востока (Е). Оси , образуют плоскость горизонта. Оси , лежат в плоскости меридиана.

Вектор скорости вращения Земли (U=15/ч) проектируется на оси , . Вертикальная составляющая скорости вращения , горизонтальная составляющая , где  - широта места расположения точки О.

Для точки О', расположенной на экваторе, истинная вертикаль  расположена в плоскости экватора и направлена по линии пересечения плоскости меридиана с плоскостью экватора.

Гирокомпас устанавливается на неподвижном относительно Земли основании так, чтобы ось Y была направлена по вертикали .

Рассмотрим работу гирокомпаса, установленного на экваторе (=0). Ось Y находится в плоскости экватора (рис.4). Ось вращения Земли, проходящая через полюса N, S, перпендикулярна плоскости чертежа.

Рис.4 Работа гирокомпаса на экваторе.

Пусть в начальный момент времени ось вращения ротора гиромотора Z горизонтальна и направлена на Восток (положение I). Сила тяжести , направленная по вертикали, не создает момента вокруг т. О_п. Гироскоп, свободный от действия моментов, сохраняет неизменное положение оси Z в инерциальном пространстве.

За некоторый промежуток времени Земля повернется вокруг своей оси, проходящей через полюса N, S, и вертикаль места расположения гирокомпаса изменит свою первоначальную ориентацию в инерциальном пространстве (положение II).

Ось гирокомпаса Z, сохраняя то положение, которое она имела в положении I, окажется поднятой над плоскостью горизонта (0). Сила тяжести создает момент вокруг т. О_п (величина G называется маятниковостью гирокомпаса). Вектор момента направлен перпендикулярно к плоскости чертежа вверх. Момент вызывает прецессию гироскопа со скоростью . Скорость прецессии вокруг вертикали равна

.

С этой скоростью ось Z поворачивается к Северу, приближаясь к плоскости меридиана.

По мере дальнейшего суточного вращения Земли ось Z продолжает подниматься над плоскостью горизонта, угол  увеличивается. При этом скорость прецессии возрастает и ось Z с возрастающей скоростью прецессирует к плоскости меридиана.

В положении III ось Z находится в плоскости меридиана, но по-прежнему поднята над плоскостью горизонта (рис.4, вид по стрелке «А»). Следовательно, проекция Н на вертикаль равна . Угол  достигает своего максимального значения.

Прецессия продолжается, ось Z выходит из плоскости меридиана и движется в сторону Запада (положение IV). Угол  начинает уменьшаться, так как плоскость горизонта как бы сама приближается к оси Z. Скорость прецессии вокруг вертикали уменьшается, но знак ее сохраняется.

Наступит такой момент времени, когда ось Z совпадет с плоскостью горизонта (положение V). Угол =0, маятниковый момент равен нулю, прецессия прекращается. ЧЭ останавливается.

При дальнейшем вращении Земли ось Z окажется ниже плоскости горизонта (положение VI). Угол  и маятниковый момент изменяют свои знаки на обратные. Скорость прецессии также изменяет свой знак и ось Z начинает вновь двигаться к плоскости меридиана.

Как показывают ниже приведенные уравнения движения гирокомпаса, ось Z совершает незатухающие колебания относительно плоскости меридиана и плоскости горизонта.

Составим укороченные (без учета инерционных и демпфирующих моментов) уравнения движения маятникового гирокомпаса на основе принципа Д`Аламбера ( ).

На рис.5 показаны моменты, действующие вокруг осей x,y.

Положим, что возмущающие моменты отсутствуют. При малых углах  ; .

Уравнения движения вокруг осей x,  получают вид:

В реальных гирокомпасах , так как , то .

Тогда уравнения получают вид:

Рис.5 Угловые скорости и моменты, приложенные к ЧЭ.

В положении равновесия, когда , имеем:

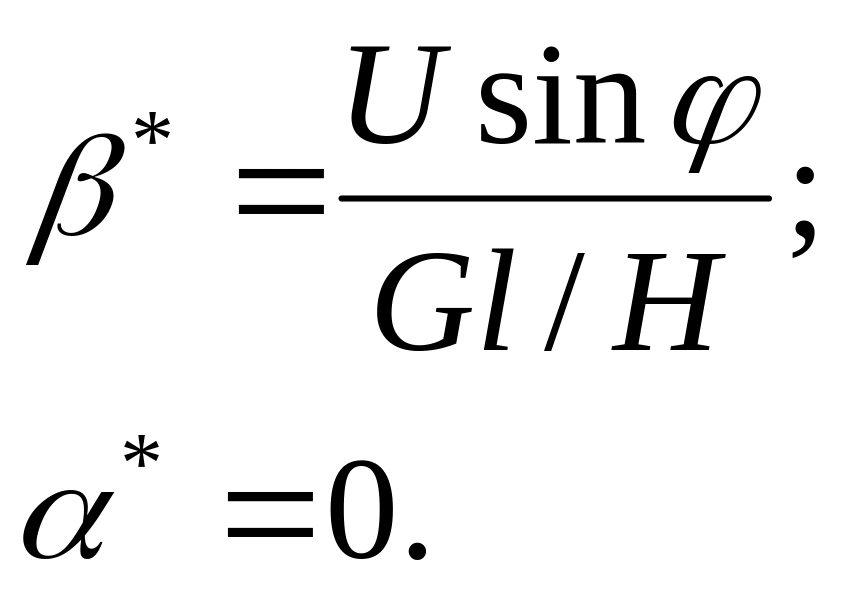
При малых углах , характеризующих отклонения оси Z от плоскости меридиана, уравнения получают вид:

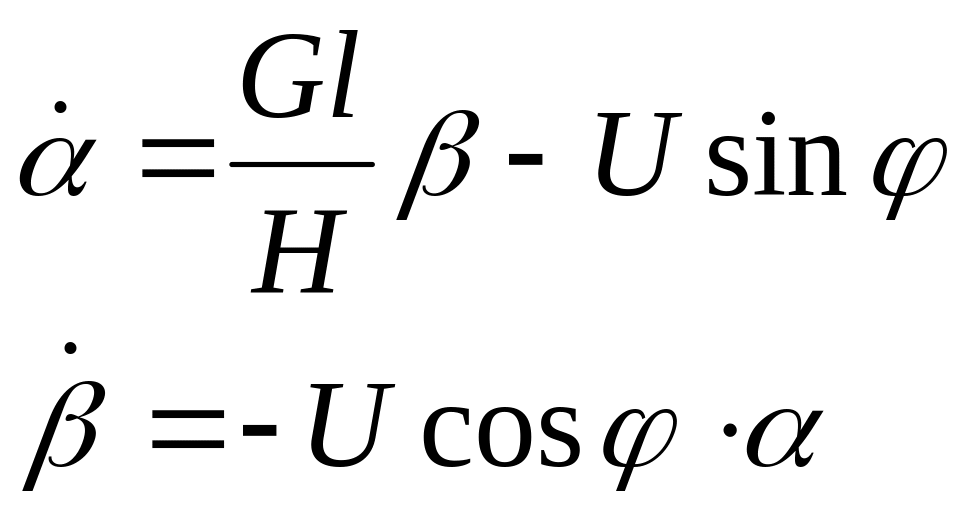(1)

После разделения переменных получим:

(2)

Решения уравнений (2) получим с использованием преобразования Лапласа при начальных условиях:

В операторном виде уравнения (1) получают вид:

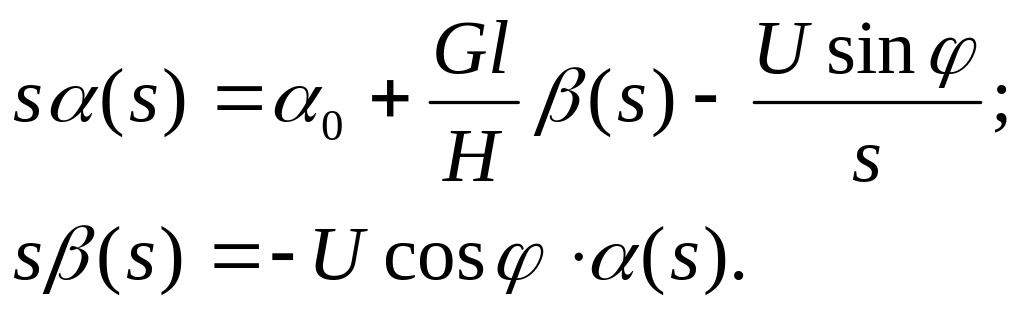
Решения имеют вид:

где (3)

Обратные преобразования имеют вид:

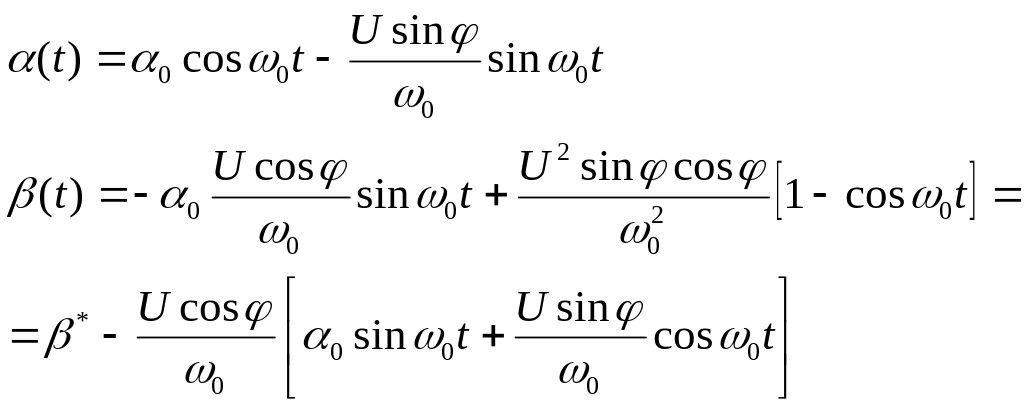
После преобразований получим:

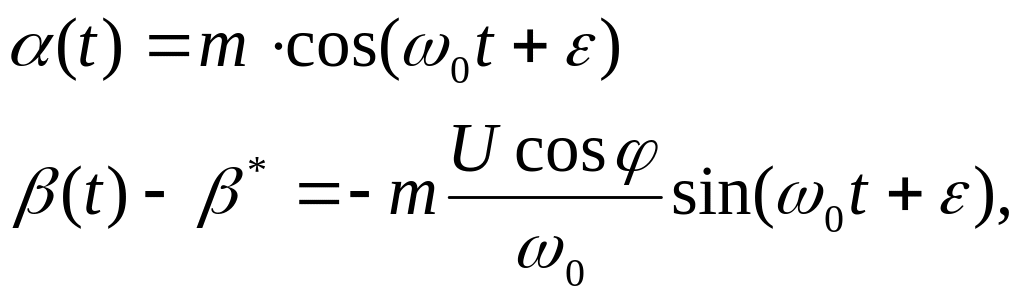
где

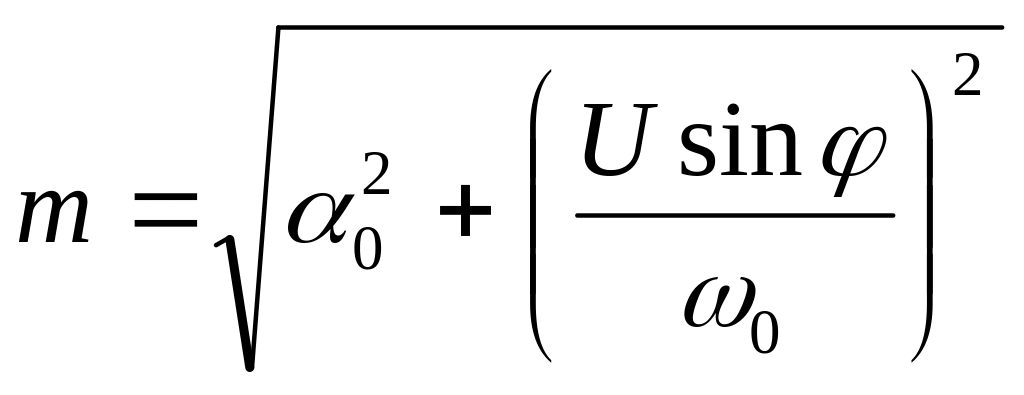
ЧЭ гирокомпаса, будучи отклоненным от плоскости меридиана на угол , совершает незатухающие колебания с частотой около положения равновесия, определяемого координатами: . Частота , определяемая формулой (3), зависит от широты .

Определим траекторию апекса гироскопа (т. А на рис.2) на картинной плоскости. Уравнение траектории получим из уравнения (4):

(5)

Уравнение (5) является уравнением эллипса с полуосями и с центром в точке О .

Отношение полуосей эллипса определяется величиной . Следовательно, эллипс сильно вытянут в горизонтальном направлении (рис.2). Малая ось находится в плоскости меридиана, большая ось – в плоскости, поднятой над плоскостью горизонта на угол .

Угол называется компенсирующим углом. При =0 .

При работе гирокомпаса углы подъема и опускания относительно плоскости горизонта малы.

В точках 1, 2 (см. рис 2) скорость прецессии равна нулю, ЧЭ останавливается. Эти положения ЧЭ называются точками реверсии и соответствуют максимальным отклонениям ЧЭ от плоскости меридиана.

Снимая отсчеты N₁, N₂ по лимбу в точках реверсии 1, 2, определяют отсчет , соответствующий линии пересечения плоскостей меридиана и горизонта, то есть направлению на Север.

Азимут (истинный курс) ориентирного направления вычисляется по формуле

,

где - поправка визуального канала, записанная в формуляре комплекта гирокомпаса.

Вид отсчетного поля зрения визуального канала гирокомпаса представлен на рис.6.

Отсчет производится в делениях угломера ДУ. Поворот лимба на 360 соответствует 6000 ДУ, что записывается в виде 60-00. 1 ДУ соответствует 0.06=3.6 угл.мин

Цена деления лимба – 5 ДУ (18 угл.мин), что записывается в виде 00-05.

Цена деления сетки визуальной отсчетной системы – 0.2 ДУ (0.72 угл.мин = 43.2 угл.с), что записывается в виде 00-00.2.

Рис.6 Поле зрения визуального канала.

Штрих лимба, попадающий на сетку, определяет целое число делений угломера. На рис. 6 отсчет по лимбу – 23-20 ДУ. Деление шкалы сетки, против которого находится штрих лимба, определяет единицы и десятые доли ДУ. На рис. 6 отсчет по сетке 00-01.4. Таким образом отсчет равен 23-21.4 ДУ.

Если один из отсчетов N₁ (или N₂) находится в первой четверти (00-00 – 15-00) ДУ, а второй N₂ (или N₁) – в четвертой четверти (45-00 – 60-00) ДУ, то вычисление азимута производится по формуле

,

знак «+», если N₁+ N₂ < 60-00

знак «-», если N₁+ N₂ > 60-00.

Поправкой гирокомпаса называется разность между истинным значением азимута ориентированного направления и средним из шести значений азимута этого же направления, определяемых с помощью гирокомпаса. Перед началом определения поправки необходимо выбрать эталонное направление, азимут которого известен с погрешностью не более 00-00.9 ДУ (3.24 угл. мин).