
МЕТОДИЧКА_EXCEL_НОВАЯ
.pdf
Рисунок 6.4 –Диалоговое окно Добавление ограничения
Рисунок 6.5 – Диалоговое окно Добавление ограничения
51
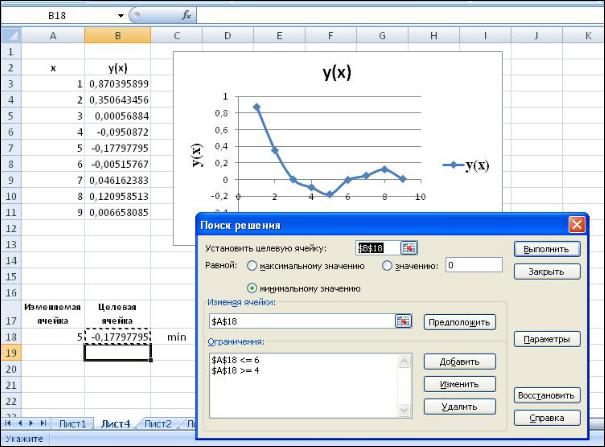
Рисунок 6.6 – Диалоговое окно Поиск решения
4. Нажатием на кнопку Параметры вызываем диалоговое окно
Параметры поиска решения (см. рис.6.7.)
Обычно установленных по умолчанию значений вполне хватает для нахождения решений большинства задач. При решении сложной задачи вы всегда можете настроить эти параметры вручную.
Для того, чтобы закрыть диалоговое окно Параметры поиска решения щелкните на кнопке OK. После заполнения всех параметров окна диалога Поиск решения нажмите кнопку Выполнить.
Значения, отображаемые в рабочем листе (ячейки A18, B18), представляют собой оптимальное решение задачи (рис. 6.8). Минимальное значение функции равно –0,21379616 в точке 4,64279. Оставляем эти значения в листе, установив переключатель Сохранить найденное решение и нажмете кнопку OK. Если требуется отчет, воспользуйтесь полем Типотчета для выбора типа отчета.
52
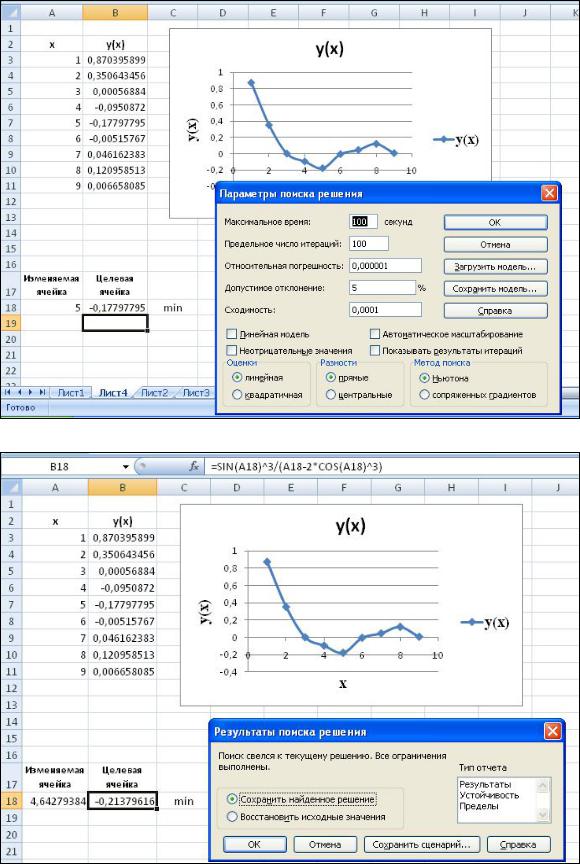
Рисунок 6.7. – Диалоговое окно Параметры поиска решения
Рисунок 6.8. – Диалоговое окно Результаты поиска решения
53
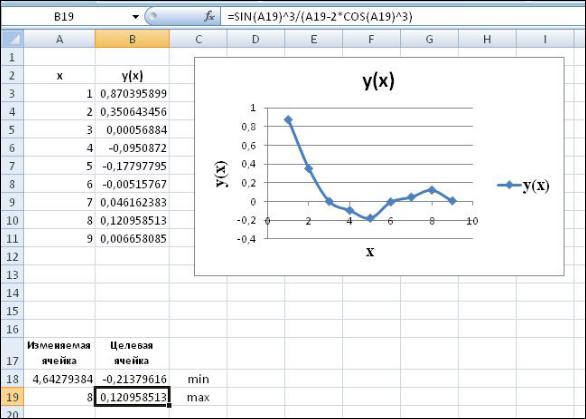
Для нахождения наибольшего значения функции y(x) в ячейке А19 задаем приближение 8, в ячейку В19 помещаем формулу
sin(A19)^3/(A19 2*cos(A19)^3). Формулу копируем из ячейки В18. (см. рис. 6.9). Далее вызываем команду Поиск решения, задаем ограничения, вызываем диалоговое окно Параметры поиска решения и
получаем результат (см. рис. 6.10– 6.14).
Максимальное значение функции = 0,1276727 в точке 7,81085.
Рисунок 6.9 – Подготовка ячеек перед вызовом команды ПОИСК РЕШЕНИЯ
54
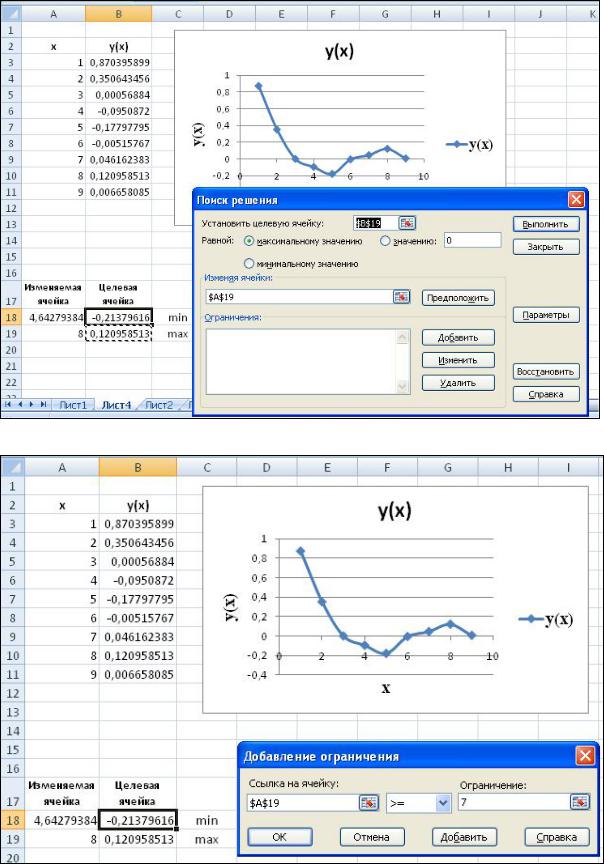
Рисунок 6.10.– Диалоговое окно Поиск решения
Рисунок 6.11– Диалоговое окно Добавление ограничения
55
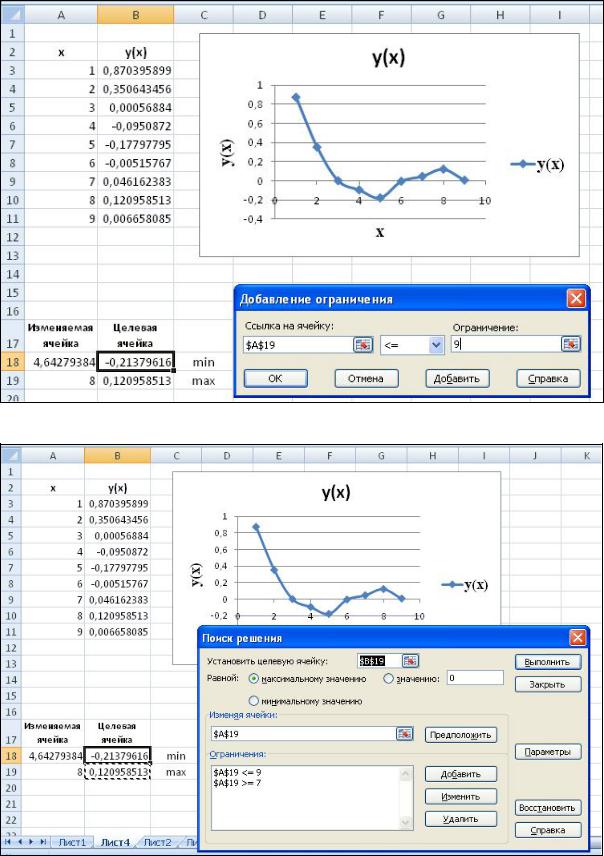
Рисунок 6.12– Диалоговое окно Добавление ограничения
Рисунок 6.13– Диалоговое окно Поиск решения
56
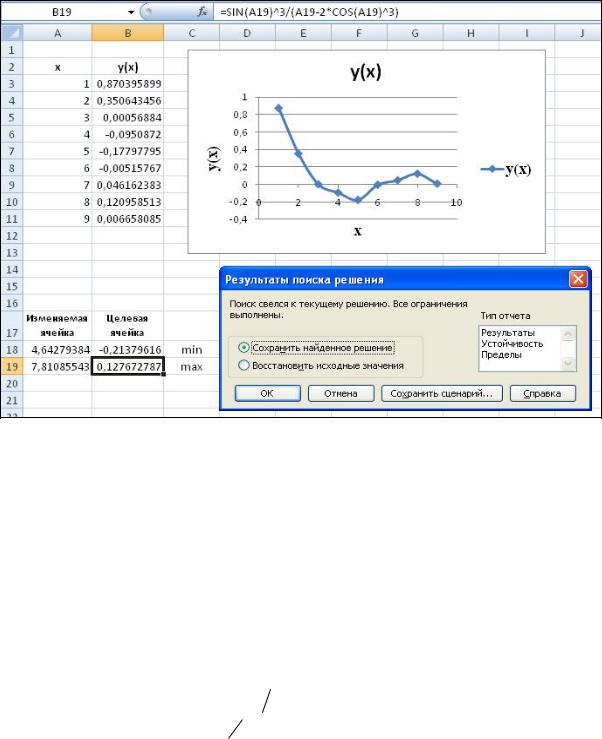
Рисунок 6.14 – Диалоговое окно Результаты поиска решения
6.2. Задачи для выполнения лабораторных работ
Найти экстремумы функции. Исходные данные представлены в табл.6.1.
Таблица 6.1 – Варианты задач
Вар. |
Функция |
Диапазон изменения x |
|
1 |
F(x) 5 x xsin(x) 7 |
1 x 15 |
h 1 |
2 |
P(x) 2 x 0,5x2cos(x) 5 |
0 x 10 |
h 0,5 |
3 |
Q(x) x 2 exsin(x) |
5 x 5 |
h 0,5 |
4 |
Y(x) 2 ln(x)2 3cos(3x) |
1 x 5 |
h 0,2 |
5 |
G(x) (cos(x)3 0,5) (x cos(x)) |
1 x 7 |
h 0,5 |
6 |
1 |
1 x 10 |
h 0,5 |
|
M(x) (4x 7) 3 3cos(x) 4 |
|
|
7 |
Q(x) 1 lg(x)sin(x) |
1 x 10 |
h 0,5 |
8 |
C(x) 1 ln(x)2 cos(x)2 |
1 x 10 |
h 0,5 |
9 |
R(x) 1 arctg(x)2 cos(x) |
1 x 10 |
h 1 |
10 |
K(x) 2 ln(x)2 sin(x) |
1 x 10 |
h 1 |
|
57 |
|
|
Тема 7 Решение систем уравнений в EXCEL 7.1 Примеры решения задач
Способ 1. С помощью обратной матрицы (для системы линейных уравнений).
Задана система линейных уравнений в виде
n |
|
|
|
aijxj |
bi , i 1,2,...,n, |
detA 0, |
(7.1) |
j 1 |
|
|
|
Матричный метод решения системы(7.1), записываемой в виде AX B, как известно, состоит в применении формулы
X A 1B,
где A– матрица системы уравнений,
A 1 – обратная ей матрица,
B– вектор правых частей уравнений, X – вектор неизвестных.
Пример 1. Решить систему линейных алгебраических уравнений:
x 2y 3z 6
2x 3y 4z 16
3x 2y 5z 12
Решение системы (7.3) матричным методом представлено на рис.7.1, 7.2, 7.3, 7.4.
(7.2)
(7.3)
Последовательность расчета:
1.В ячейки A3:C5 вводим матрицу системы уравнений (7.3).
2.В ячейки G3:G5 вводим вектор правых частей системы уравнений (7.3).
3.Для получения обратной матрицы выделяем диапазон ячеек A8:С10, где будет обратная матрица и устанавливаем курсор ввода в окне формул.
4.Открываем диалоговое окно МОБР (рис.7.1 ). Заполним поле «Массив», не нажимаем клавишу «ОК»
5.< Ctrl> + <Shift > + < Enter >
8. Получили обратную матрицу в ячейках A8:C10 (рис.7.2)
58
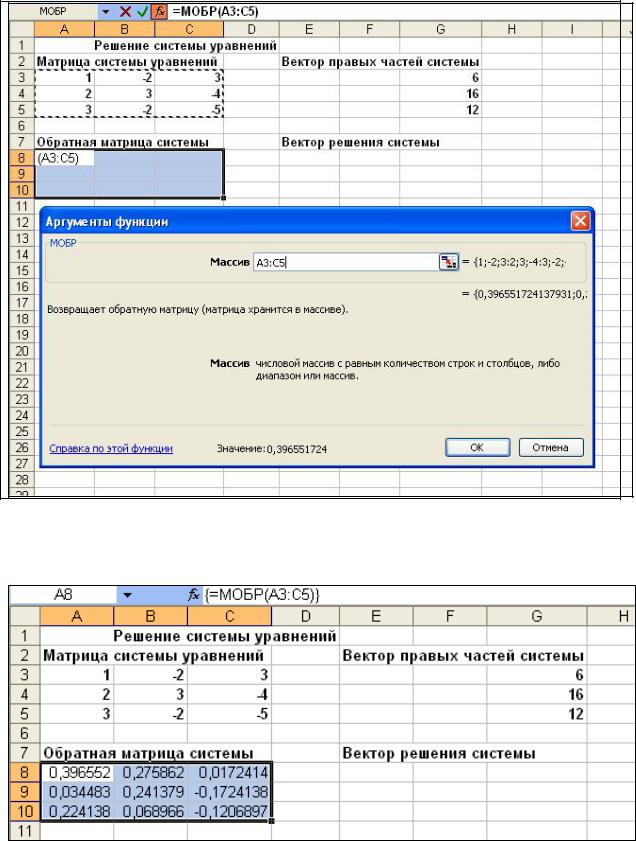
Рис.7.1
Рис.7.2
59
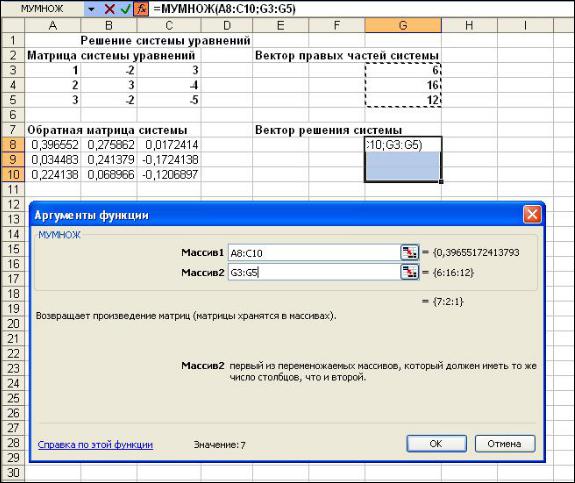
9. Затем умножаем обратную матрицу на вектор правых частей
(рис.7.3, 7.4)
Для этого
1)выделяем диапазон свободных ячеек G8:G10 для получения вектора решения системы и устанавливаем курсор ввода в окне формул.
2)открываем диалоговое окно встроенной функции умножения матриц МУМНОЖ (рис.7.3) и на его полях указываем диапазоны перемножаемых матриц. Не нажимаем клавишу «ОК».
3) < Ctrl> + <Shift > + < Enter >
Получили вектор решения системы в ячейках G8:G10 (рис.7.4)
Рис.7.3
60
