Северин Методы БМ

Возвращаясь к исходным обозначениям по равенствам (5.3)–(5.5), получим окончательно модифицированную формулу БФГШ (4.35)

ставляющий собой вектор с i -той единичной проекцией и остальными нулевыми проекциями. Вычислим разность i f f (x0 ei ) f (x0 )

151

и составим отношение i f . Если существует предел

то он называется частной производной функции f (x) по переменной xi в точке x0 и обозначается f (x0 ) xi .

Итак, по определению

Частные производные вычисляются по обычным правилам и формулам дифференцирования, причем при вычислении f xi диф-

ференцирование ведется по переменной xi , а остальные переменные считаются неизменными.

Частные производные функции двух переменных f (x1, x2 ) геометрически представляют собой тангенсы углов наклона касательных к сечениям графика этой функции плоскостями x1 C и x2 C .

Если для функции f (x) в точке x0 существуют все частные производные первого порядка, то она называется дифференцируемой в

Символ «набла» служит для обозначения оператора градиента

152

( x1 , x2 , , xn )T . Градиент также обозначается через g(x)

. Вектор градиента определяет направление наиболее быстрого возрастания функции в данной точке.

Поскольку по определению градиента xi ei , то

xT (x1, x2, , xn ) (e1, e2, ...,en ) E .

Если векторы-столбцы u и v зависят от x , то по правилу производной произведения функций

(uT v) (uT )v (vT )u .

Пусть функция f (x) имеет частные производные f xi , i 1, n . Предположим, что эти частные производные в свою очередь диффе-

Дифференцируя f xi по другой переменной x j , получим сме-

шанную частную производную второго порядка, которая обозначается

153

Пусть функция f (x) является дважды дифференцируемой по всем переменным. Тогда для такой функции можно составить матрицу вторых частных производных, которая называется матрицей Гессе

Поэтому матрица Гессе является симметрической матрицей и для нее

2 f (x)T 2 f (x) .

Матрица Гессе также обозначается как H(x) .

5.6. Формула Тейлора

Пусть функция f (x) скалярного действительного аргумента x R в любой точке x0 n раз дифференцируема. Тогда для нее справедлива формула Тейлора

f (x h) f (x) f (x)h 21! f (x)h2 n1! f (n) (x)hn o(hn ) ,

где h – приращение аргумента, o(hn ) – бесконечно малая более вы-

сокого порядка, чем hn , называемая остаточным членом формулы

154

Тейлора в форме Пеано.

Пусть теперь функция f (x) векторного аргумента x Rn в любой точке дважды дифференцируема. Тогда для нее формула Тейлора

где h (h1, h2 , , hn )T – векторное приращение аргумента. Эту формулу можно представить в векторном виде

f (x h) f (x) f (x)T h 21!hT 2 f (x)h o( h 2 ) ,

где f (x) и 2 f (x) – градиент и матрица Гессе функции f (x) соответственно.

квадратной матрицы A с элементами aij , квадратичную форму можно

представить в виде

f (x) xT Ax .

Без потери общности матрицу A можно всегда предполагать симметрической. В противном случае A следует заменить симметрической

матрицей (A AT )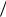2 , значения квадратичной формы при этом не изменятся.

155

Симметрическая матрица A называется неотрицательно определенной, если xT Ax 0 для всех x Rn . При этом пишут A 0 .

Симметрическая матрица A называется положительно определенной, если xT Ax 0 для всех x 0 . При этом пишут A 0 .

Симметрическая матрица A называется неположительно определенной, если xT Ax 0 для всех x Rn . При этом пишут A 0 . Матрица A неположительно определенная тогда и только тогда, когдаA есть неотрицательно определенная матрица.

Симметрическая матрица A называется отрицательно определенной, если xT Ax 0 для всех x 0 . При этом пишут A 0 . Матрица A отрицательно определенная тогда и только тогда, когда A – положительно определенная матрица.

Симметрическая матрица A называется неопределенной, если квадратичная форма xT Ax может принимать как положительные, так и отрицательные значения.

Для установления положительной определенности матрицы A составим из ее элементов определители

an1 an2 ann

Очевидно, det A n . Определители 1 , 2 , 3 , …, n 1 называют-

ся главными диагональными минорами матрицы A .

К р и т е р и й С и л ь в е с т р а – Я к о б и . Для того, чтобы квад-

ратная симметрическая матрица была положительно определенной,

156

необходимо и достаточно, чтобы все ее главные диагональные миноры, включая и определитель матрицы, были положительными.

Таким образом, если для матрицы A имеем 1 0 , 2 0 ,3 0 , …, n 1 0 , n 0 , то A – положительно определенная матрица. Все диагональные элементы положительно определенной матрицы должны быть положительными.

Чтобы установить, что матрица является отрицательно определенной, следует умножить ее на 1 и проверить полученную матрицу на положительную определенность. Тогда из критерия СильвестраЯкоби следует, что для того, чтобы матрица была отрицательно определенной, необходимо и достаточно, чтобы знаки ее главных диагональных миноров, включая и определитель этой матрицы, чередовались, начиная со знака «–». То есть, если 1 0 , 2 0 , 3 0 , …,

( 1)n n 0 , то A – отрицательно определенная матрица. Все диагональные элементы отрицательно определенной матрицы должны быть отрицательными.

При проверке матрицы на неотрицательную определенность достаточно установить, что все ее диагональные элементы и все главные диагональные миноры, включая определитель матрицы, неотрицательны.

При проверке матрицы на неположительную определенность достаточно установить, что все ее диагональные элементы и все главные диагональные миноры, включая определитель матрицы, неположительные.

При проверке матрицы на неопределенность достаточно убедиться в том, что, по крайней мере, два из ее диагональных элементов имеют разные знаки.

157

учеб. пособ. / А. В. Пантелеев, Т.А. Летова. – М. : Высш. шк., 2002. –

544с.

13.Раскин Л.Г. Математическое программирование : учебнометод. пособ. / Л.Г. Раскин. – Харьков : ПП «ГЕММА», 1986. – 68 с.

14.Реклейтис Г. Оптимизация в технике : в 2 кн. / Г. Реклейтис,

А. Рейвиндран, К. Рэгсдел. Кн. 1 ; пер. с англ. В.Я. Алтаева, В.И. Моторина. – М. : Мир, 1986. – 349 с.

15.Северин В.П. Методы одномерного поиска : учебно-метод. пособ. по курсу «Методы оптимизации» / В.П. Северин. – Х. : НТУ

«ХПИ», 2012. – 112 с.

16.Струченков В.И. Методы оптимизации. Основы теории, зада-

чи, обучающие компьютерные программы : учеб. пособ. / В.И. Струченков. – М. : Экзамен, 2005. – 256 с.

17.Сухарев А.Г. Курс методов оптимизации : учеб. пособ. / А.Г. Сухарев, А.В. Тимохов, В.В. Федоров. – 2-е изд. – М. : ФИЗМАТ-

ЛИТ, 2005. – 368 с.

18.Форсайт Д. Машинные методы математических вычислений / Д. Форсайт, М. Малькольм, К. Моулер ; пер. с англ. Х.Д. Икрамова. –

М. : Мир, 1980. – 280 с.

19.Химмельблау Д. Прикладное нелинейное программирование / Д. Химмельблау ; пер. с англ. И.М. Быховской, Б.Т. Вавилова. – М. :

Мир, 1975. – 536 с.

20.Fletcher R. Practical methods of optimization / R. Fletcher. – 2-d edition. – UK, Chichester : John Wiley & Sons Ltd, 2000. – 436 p.

21. Luenberger D. G. Linear and nonlinear programming / D.G. Luenberger, Y. Yinyu. – 3-d edition. – USA, New York : Springer, 2008. – 546 р.

22.Bazaraa M.S. Nonlinear programming : theory and algorithms / M.S. Bazaraa, H.D. Sherali, C.M. Shetty. – 3-d edition. – USA, Hoboken, New Jersey : John Wiley & Sons Inc., 2006. – 853 р.

23.Sun W. Optimization theory and methods. Nonlinear programming

/W. Sun, Y. X. Yuan. – USA, New York: Springer, 2006. – 687 р.

159