Северин Методы БМ

справа на матрицу S 1 , получим GnH E , откуда Gn H 1 . Поэтому следующая итерация метода Бройдена является итерацией метода Ньютона и приведет к точке минимума квадратичной функции.

Заметим, что в доказательстве этого свойства не используется условие точного одномерного поиска.

С в о й с т в о 5 . Если при минимизации квадратичной функции с положительно определенной матрицей Гессе H методом Бройдена выполняется точный одномерный поиск, то направления поиска s0 ,

s1 , …, sn 1 являются H -сопряженными.

Д о к а з а т е л ь с т в о . При выполнении условий данного утвер-

Докажем это свойство методом математической индукции. При k 1 с учетом (4.14) имеем:

sT0 Hs1 sT0 H 1d1 sT0 H(1G1g1) 1sT0 HG1g1 1(G1Hs0 )T g1 .

Отсюда по свойству 3 в виде G1p0 s0 и по условию точного одно-

мерного поиска (3.7) в виде sT0 g1 0 получим:

k 1(Gk 1Hsi )T gk 1 k 1(Gk 1pi )T gk 1 .

111

Очевидно, что

gk 1 gi 1 (gi 2 gi 1) (gi 3 gi 2 ) (gk 1 gk ) .

С учетом обозначений (4.3) имеем:

По условию точного одномерного поиска (3.7) в виде sT g 0 и сде-

i i 1

ланного предположения индукции (4.16) окончательно получим для

i 0, k условие сопряженности sT Hs 0 . Следовательно, равен-

i k 1

ства (4.16) выполняются для всех k 1, n 1.

Это свойство показывает, что метод Бройдена является методом сопряженных направлений, поэтому он минимизирует квадратичную функцию с положительно определенной матрицей Гессе H при выполнении точного одномерного поиска не более чем за n итераций.

В случае, когда целевая функция не является квадратичной, применение уравнения (4.10) может привести к нежелательным явлениям. Во-первых, матрица G k может перестать быть положительно опреде-

ленной. Во-вторых, поправка Gk может стать неограниченной. В-

третьих, если направление sk случайно совпадет с направлением

112

предыдущей итерации, матрица Gk 1 становится вырожденной или неопределенной. В алгоритме Бройдена это тоже будет иметь место, если либо Gk pk sk , либо (sk Gk pk )T pk 0 . Тогда знаменатель формулы (4.10) обращается в нуль. Эта особенность снижает надежность метода Бройдена.

4.4. Метод Девидона – Флетчера – Пауэлла

По аналогии с формулой (4.9) коррекции ранга один рассмотрим формулу коррекции ранга два

Для системы линейных алгебраических уравнений (4.5) получим

(Gk uuT vvT )pk sk .

Раскрывая скобки, после преобразований имеем

Gk pk (uT pk )u (vT pk )v sk ,

где скобки содержат скалярные величины. Это уравнение превратится

Эта формула называется формулой Девидона – Флетчера – Пауэлла

(ДФП), а использующий ее квазиньютоновский метод называется ме-

тодом Девидона – Флетчера – Пауэлла. Формула (4.14) впервые пред-

ставлена в 1959 году американским математиком В. Девидоном как часть метода оптимизации, а в 1963 году метод, основанный на фор-

113

муле (4.20), развит английскими математиками Р. Флетчером и М. Д. Д. Пауэллом. Таким образом, метод ДФП основан на формулах (4.3), (4.7), (4.8) и (4.20). Как и в методе Бройдена первая итерация начинается из заданной начальной точки x0 , и в направлении антиградиента выполняется одномерный поиск:

Последующие итерации для k 1, 2, 3, выполняются по формулам:

Выходной параметр x – конечная точка поиска.

3.Положить x x s , gy gx .

4.Вычислить gx f (x) , p gx gy , v G p .

5.Положить G G s sT (sT p) v vT (vT p) .

6.Вычислить d G gx .

114

7.Если s , то перейти к шагу 2.

8.Остановиться.

Пр и м е р 4 . 3 . Для вычисления точки минимума квадратичной функции (1.3) с допустимой погрешностью 10–3 метод Девидона – Флетчера – Пауэлла затратил 3 итерации и 19 вычислений функции. При этом траектория минимизации квадратичной функции методом ДФП такая же, как и траектория минимизации этой же функции методом Бройдена из примера 4.1, представленная на рис. 4.1.

Пр и м е р 4 . 4 . На рис. 4.3 представлена траектория минимизации функции Розенброка методом Девидона – Флетчера – Пауэлла. Одномерный поиск с начальным единичным шагом производился комбинацией метода Свенна и метода квадратичной интерполяции с тремя точками при допустимой погрешности шага 10–5. Для нахождения точки минимума с допустимой погрешностью 10–3 метод ДФП использовал 17 итераций и 265 вычислений функции. Траектория минимизации такая же, как и траектория метода Бройдена из примера 4.2, представленная на рис. 4.2.

Рис. 4.3. Минимизация функции Розенброка методом ДФП

115

4.5. Свойства метода Девидона – Флетчера – Пауэлла

В правой части этого равенства первое слагаемое неотрицательно в силу неравенства Коши – Буняковского – Шварца aT b a b , а

116

второе слагаемое неотрицательно, если sTk pk 0 . Покажем, что эти слагаемые не могут одновременно обращаться в нуль. Если первое

условии точного одномерного поиска (3.7) в виде sT g 0 и обеспе-

k k 1

чении sk как направления спуска, для которого sTk gk 0 . Действи-

тельно, в силу равенств (4.22) и (4.24) sk kGkgk , k 0 . Поэтому

sT p sT (g g ) sT g sT g sT g gT G g 0 .

k k k k 1 k k k 1 k k k k k k k k

Свойство сохранения положительной определенности матрицы G k

гарантирует, что направление dk является направлением спуска.

С в о й с т в о 3 . При минимизации квадратичной функции с по-

G1Hs0 s0 . Отсюда по формулам (4.24) с точным одномерным поиском получим:

sT0 Hs1 sT0 H 1d1 sT0 H(1G1g1) 1(G1Hs0 )T g1 1sT0 g1 0 .

Таким образом, равенства (4.25) и (4.26) выполняются при начальных значениях k 0 и k 1 соответственно.

117

Предположим, что равенства (4.25) и (4.26) выполнены для неко-

Применяя формулу (4.18) для градиента квадратичной функции, имеем

По условию точного одномерного поиска (3.7) в виде sT g 0 и сде-

i i 1

pk 1 Hsk 1 , предположения индукции (4.25) и доказанного равенства

sTi Hsk 1 0 для i 0, k имеем:

118

справедливость равенств (4.25) для произвольного k .

Это свойство показывает, что в силу равенств (4.26) метод ДФП является методом сопряженных направлений, поэтому он минимизирует квадратичную функцию с положительно определенной матрицей Гессе H при точном одномерном поиске не более чем за n итераций.

С в о й с т в о 4 . При минимизации квадратичной функции с положительно определенной матрицей Гессе H методом ДФП с точ-

ным одномерным поиском после n итераций Gn H 1 .

Д о к а з а т е л ь с т в о . При сделанных предположениях после n итераций метода ДФП в силу выполнения равенств (4.26) при k n 1 векторы s0 , s1 , …, sn 1 являются сопряженными. Поэтому по лемме 3.1 они линейно независимы. Представим их столбцами невырожденной матрицы S . Поскольку при этом выполняются равенства (4.25)

женными и линейно независимыми. Сформируем из них невырожденную матрицу S . Из условий сопряженности (4.26) ST HS D , где D –

диагональная матрица с элементами sTi Hsi . Поэтому H (ST ) 1DS 1 .

Тогда H 1 SD 1ST , где D 1 – диагональная матрица с элементами

119

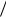
1 (sTi Hsi ) . Перемножим матрицы в правой части последнего равенства

Отсюда с использованием свойства квадратичной функции (4.4) в виде pi Hsi получим равенство (4.27).

Представим формулу ДФП (4.20) в виде

Gk 1 Gk Ak Bk ,

где

Отсюда следует, что начальное задание аппроксимирующей матрицы G0 E в процессе минимизации квадратичной функции компенсируются последней дробью в формуле (4.20).

Приведенные свойства метода Девидона – Флетчера – Пауэлла проявляются и при минимизации дифференцируемой целевой функции общего вида.

Вычислительные эксперименты, проведенные многими исследователями, показали, что метод Девидона – Флетчера – Пауэлла очень чувствителен к точности одномерного поиска. Если одномерная минимизация целевой функции проводится с невысокой точностью, то эффективность этого метода снижается.

120