6.4. Стохастические модели управления запасами

Предположим, что спрос за интервал времениявляется случайным и задан его закон распределения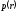или плотность вероятностей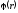(обычно функци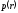ии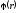оцениваются на основании опытных или статистических данных). Если спросниже уровня запаса, то приобретение (хранение, продажа) излишка продукта требует дополнительных затрат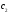на единицу продукта; наоборот, если спросвыше уровня запаса, то это приводит к штрафу за дефицитна единицу продукции.

В качестве функции суммарных затрат, являющейся в стохастических моделях случайной величиной, рассматривают ее среднее значение или математическое ожидание.

В рассматриваемой модели при дискретном случайном спросе , имеющем закон распределения, математическое ожидание суммарных затрат имеет вид:

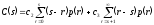. (6.14)

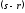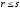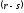В выражении (6.14) первое слагаемое учитывает затраты на приобретение (хранение) излишка единиц продукта (при), а второе слагаемое – штраф за дефицит наединиц продукта (при ).

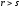В случае непрерывного случайного спроса, задаваемого плотностью вероятностей 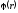, выражение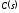принимает вид:

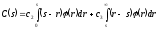. (6.15)

Задача управления запасами состоит в отыскании такого запаса , при котором математическое ожидание суммарных затрат (6.14) или (6.15) принимает минимальное значение.

Можно доказать, что при дискретном случайном спросе выражение (6.14) минимально при запасе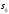, удовлетворяющем неравенствам

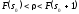, (6.16)

а при непрерывном случайном спросе выражение (6.15) минимально при значении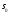, определяемом из уравнения

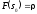, (6.17)

где

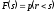
есть функция распределения спроса ,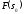и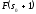– ее значения;плотность убытков из-за неудовлетворенного спроса, определяемая по формуле (6.12).

Лабораторная работа №10 Модели управления запасами

Задача 1.

Интенсивность поступления деталей на склад готовой продукции цеха составляет в начале смены 5 дет./мин, в течение первого часа линейно возрастает, достигая к концу его 10 дет./мин, и затем остается постоянной. Полагая, что поступление деталей на склад происходит непрерывно в течение всех семи часов смены, а вывоз деталей со склада производится только в конце работы, записать выражение для уровня запаса в произвольный момент времени и, используя его, найти количество деталей на складе: а) через 30 мин после начала работы; б) в конце смены.

Решение

По условию в течение смены не происходит выдачи деталей со склада, т.е. 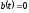. Интенсивность пополнения запаса в течение первого часа линейно возрастает, т.е.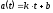. Учитывая, что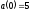, получаем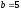. Так как в конце часа, т.е. при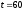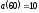, то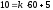, откуда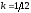. Таким образом, для первого часа смены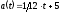, а затем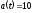. Учитывая продолжительность смены (7 ч = 420 мин) и соотношение (6.2), получим:

если

,

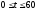
если

.

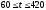
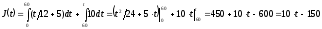Количество деталей на складе через 30 мин после начала работы: , а в конце смены:.

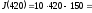
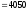Задача 2.

Потребность сборочного предприятия в деталях некоторого типа составляет 120000 деталей в год, причем эти детали расходуются в процессе производства равномерно и непрерывно. Детали заказываются раз в год и поставляются партиями одинакового объема, указанного в заказе. Хранение детали на складе стоит 0,35 ден. ед. в сутки, а поставка партии – 10000 ден. ед. Задержка производства из-за отсутствия деталей недопустима. Определить наиболее экономичный объем партии и интервал между поставками, которые нужно указать в заказе.

Решение

По условию затраты на одну партию составляют 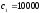ден. ед., затраты хранения единицы запаса в сутки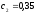ден. ед. Общий промежуток времени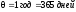, а общий объем запаса за этот период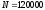деталей. По формуле (6.6)деталей, а по формуле (6.7)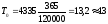дней.

Задача 3.

Для условия задачи 2 найти наиболее экономичный объем партии и интервал между поставками, если известно, что отсутствие на сборке каждой детали приносит в сутки убытки в размере 3,5 ден. ед.

Решение

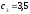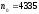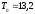По условию . Ранее (при решении задачи 1) было получено, чтои. По формуле (6.12) найдем плотность убытков из-за неудовлетворенного спроса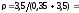0,909, т.е. 9,1% времени между поставками детали на сборке будут отсутствовать.

Теперь по формуле (6.13) определим оптимальный размер партии 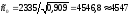. В силу (6.7) пропорционально увеличению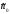должен увеличится интервал между поставками, т.е.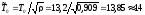дней.

Задача 4.

Предприятие закупает агрегат с запасными блоками к нему. Стоимость одного блока равна 5 ден. ед. В случае выхода агрегата из строя из-за поломки блока, отсутствующего в запасе, простой агрегата и срочный заказ нового блока к нему обойдется в 100 ден. ед. Необходимо определить оптимальное число запасных блоков, которое следует приобрести вместе с агрегатом при условии непрерывного случайного спроса ,распределенного по показательному закону с функцией распределения 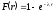при.

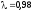Решение

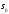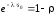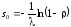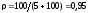Оптимальное число запасных блоков найдем из уравнения (6.17): , откудаи. Найдем плотность убытков из-за неудовлетворенного спроса . Итак,

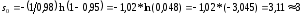(блока).