2 Векторларды оқыту әдістемесі
2.1 Векторларға қолданылатын амалдар
Айталық,
қандай да бір денені А нүктесінен В
нүктесіне, сонан соң В нүктесінен С
нүктесіне жылжытайық. Мұнда дененің
орын ауыстыруын (қозғалысын) параллель
көшіру
және
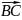векторларымен анықтала отырып, А
нүктесіндегі денені С нүктесіне
көшіретінін байқаймыз. Онда бұл
қозғалыстың нәтижесін
векторымен көрсетуге болады (15-сурет).
(15-сурет).
Ал
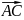векторымен көрсетуге болады. Ал
векторымен анықталатын параллель көшіру
және
векторларымен анықталатын параллель
көшірулерді бірінен соң бірін қолдану
арқылы анықталғандықтан,
векторын
және
векторларының қосындысы ретінде
қарастыруға болады:
Осы сияқты, кез келген екі вектордың қосындысы анықталады.
Анықтама
1.
және
векторлары берілсін. Жазықтықтан А
нүктесін белгілеп, осы нүктеден
на тең
векторын, ал В нүктесінен
на тең
векторын саламыз. Осының нәтижесінде
шығатын
векторын
және
векторларының қосындысы
деп атаймыз:
(16-сурет).
(16-сурет).
Векторларды қосудың бұл ережесін үшбұрыш ережесі деп атайды.
Енді векторларды қосу амалы анықтамада көрсетілген А нүктесін таңдап алуымызға тәуелсіз екенін көрсетейік.
Басқаша
айтқанда,
және
теңдіктерінен
теңдігі шығатынын көрсету қажет.
Шынында
да,
теңдігінен жоғарыда келтірілген 1-
салдар бойынша
теңдігі орындалады. Осы сияқты,
теңдігін аламыз. Осыдан
.
Онда жоғарыдағы 1-салдар бойынша
теңдігі орындалуы керек (17-сурет).
(17-сурет).
Векторларды
қосудың үшбұрыш ережесі бойынша әрбір
векторы үшін
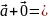теңдігі орындалатынын көреміз.
Сонымен
қатар, кез келген А, В, С нүктелері үшін
теңдігі орындалатыны да үшбұрыш
ережесінен шығады. Мұнда А, В, С нүктелері
бір-бірімен беттесуі де мүмкін.
Теорема1.
Кез
келген
және
векторлары үшін:
(ауыстырымдылық
заңы);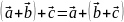
(терімділік
заңы) орындалады.
Дәлелдеу.
және векторлары коллинеар емес болсын. Жазықтықтан А нүктесін белгілеп, осы нүктеден
және
векторларын салайық. Онда төмендегі
18-суретте көрсетілгендей АВСD
параллелограмын аламыз.
(18-сурет).
Үшбұрыш ережесі бойынша
Осы сияқты,
Осыдан теңдігі шығады.
Егер
және
векторлары коллинеар болса, онда
және
векторлары бір түзудің бойында жатады.
Онда
және
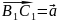векторлары да осы түзудің бойында
жатады. С және
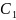нүктелерінің беттесетінін дәлелдеу
керек. Егер
болса, онда С және
нүктелерінің беттесетіндігі шығады
(19-сурет).
(19-сурет).
Ал
болса, онда С және
нүктелерінің беттесуі кесінділерді
азайту ережесінен шығады (20-сурет).
(20-сурет).
А нүктесін белгілеп,
және
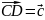векторларын саламыз (21-сурет).
(21-сурет).
Онда
Екінші жағынан,
Осыдан теңдігін аламыз. Теорема толық дәлелденді.
1-қасиеттің
дәлелденуіне
және
векторларының коллинеар емес жағдайында
қосындысы параллелограмның диагоналы
арқылы анықталатынын көрдік, яғни
және
векторларының қосындысын анықтау үшін
қандай да бір А нүктесінен
және
векторларын салып, оны АВСD параллелограмына
дейін толықтырғанда
болатынын көрдік. Векторларды қосудың
бұл ережесін параллелограмм
ережесі
деп атайды. Параллелограмм ережесін
көбінесе физикада, мысалы, екі күшті
қосу кезінде пайдаланады.
Векторларды
қосудың ауыстырымдылық және терімділік
заңдылықтарынан бірнеше векторлардың
қосындысындағы қосылғыштардың орындарын
қалауымызша ауыстырып, топтауымызға
болатындығы шығады. Бұл бірнеше
векторларды (екіден көп) қосуды
жеңілдетеді. Айталық,
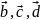векторларын
қосайық (22-сурет).
(22-сурет).
Онда
қандай да бір А нүктесінен бастап
және
векторларын
саламыз. Онда АВСDЕ сынық сызығының басы
мен соңғы нүктелерін қосатын
векторы берілген
және
векторларының қосындысы болады:
Анықтама
2.
және
векторларының
айырмасы
деп
векторымен қосындысы
векторына тең болатын векторды айтады.
және
векторларыныңайырмасын
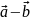арқылы белгілейді.
және
векторларының айырмасын былай салады:
қандай да бір О нүктесінен бастап
және
векторларын саламыз. Онда
векторы
айырмасына тең (23-сурет).
(23-сурет).
Себебі,
теңдігі орындалады. Сондықтан
деп жазыға болады. Суретте
айырмасының стрелкасын
векторының ұшына қаратып салады.
Нөлдік
емес әрбір
векторы үшін
және
шарттарын қанағаттандыратын
векторын
векторына қарама-қарсы вектор деп
атаймыз.
ға қарама-қарсы векторды –
арқылы белгілейді:
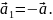Нөлдік вектор өзіне өзі қарама-қарсы
болады деп есептелінеді. Төмендегі
23- суретте
векторы
векторына қарама-қарсы. Осыдан,
қарама-қарсы векторлардың қосындысы
нөлдік вектор болғандығын көреміз:
Бұған кері тұжырым да орындалаты, яғни егер екі вектордың қосындысы нөлдік вектор болса, онда бұл векторлар бір-біріне қарама-қарсы болады.
Шынында
да, егер
болса, онда
және
болады, яғни
мен
қарама-қарсы векторлар.