
- •Курстық жұмыс
- •Қазақстан Республикасы Білім және ғылым министрлігі
- •Тараз мемлекеттік педагогикалық университеті
- •“Математика және моә” кафедрасы
- •Тапсырма
- •Тараз мемлекеттік педагогикалық университеті «Математика және моә» кафедрасы
- •Курстық жұмысты қорғайтын пән:
- •Мазмұны үшбұрыштар теңдігі белгісін оқыту әдістемесі
- •1 Вектор
- •1.1 Вектор ұғымы.
- •1.2 Векторлардың теңдігі
- •2 Векторларды оқыту әдістемесі
- •2.1 Векторларға қолданылатын амалдар
- •2.2 Векторларға берілген есептерді сабақта қолдану
- •Оқыту үрдісінің маңыздылығы:
- •Жаңа тапсырмаларды қалыптастыру:
- •Тест жұмыстары:
- •Қорытынды
- •Пайдаланылған әдебиеттер тізімі:
1.2 Векторлардың теңдігі
Жалпы, нөлдік векторды кез келген векторға колинеар деп есептейміз. Бұлай деп есептеуіміздің мағынасы келесі тақырыптарда белгілі болады.
Бағыттас векторлардың төмендегідей қасиеттері бар:
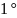 .
Егер
және
.
Егер
және
 болса, онда
болса, онда
 болады.
болады.
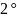 .
Егер
.
Егер
 және
және
 болса, онда
болады.
болса, онда
болады.
Дәлелдеуі.
1.
және
болғандықтан,
және
 векторларының колинеар болатындығы
шығады (егер екі түзу үшінші түзуге
параллель болса, онда бұл түзулер өзара
параллель болады). Ал
және
векторларының колинеар болатындығы
шығады (егер екі түзу үшінші түзуге
параллель болса, онда бұл түзулер өзара
параллель болады). Ал
және
 ның бағыттары
векторының бағытымен бірдей болғандықтан,
және
векторларыныңбағыттары да бірдей
болады. 2-қасиет те осылай дәлелденеді
(6-сурет).
ның бағыттары
векторының бағытымен бірдей болғандықтан,
және
векторларыныңбағыттары да бірдей
болады. 2-қасиет те осылай дәлелденеді
(6-сурет).

(6-сурет).
Анықтама 2. Егер векторлар бағыттас және олардың ұзындықтары (модульдері) тең болса, онда бұл векторларды тең векторлар деп атаймыз.
Басқаша
айтқанда, егер
және
 болса, онда
және
векторлары тең
деп аталады және оны былай жазады:
болса, онда
және
векторлары тең
деп аталады және оны былай жазады:

Айталық,
 және
және
 фигуралары берілсін. Егер кез келген
фигуралары берілсін. Егер кез келген
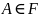 нүктесі мен
нүктесі мен
 векторы үшін
векторы үшін
 нүктесі табылып,
нүктесі табылып,
 теңдігі орындалса, онда
фигурасын
теңдігі орындалса, онда
фигурасын
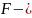 ті
векторына параллель
көшіру
арқылы алынды деп атайды (7-сурет).
ті
векторына параллель
көшіру
арқылы алынды деп атайды (7-сурет).

(7-сурет).
фигурасының векторы көмегімен фигурасына көшуін векторына параллель көшіру кезінде:
 түзуі
түзуі
 болғанда өзіне параллель түзуіне көшеді
(8-сурет),
болғанда өзіне параллель түзуіне көшеді
(8-сурет),

(8-сурет).
ал
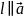 болғанда өзіне-өзі көшеді (9-сурет);
болғанда өзіне-өзі көшеді (9-сурет);

(9-сурет).
әрбір кесінді өзіне тең және параллель кесіндіге (10-сурет)

(10-сурет).
(немесе өзімен бір түзу бойында жататын кесіндіге (11-сурет))

(11-сурет).
көшеді.
Жалпы параллель көшіру түрлендіруінің осыған баламен анықтамасы мен қасиеттерін толығымен қарастырамыз.
Векторлар теңдігінің қасиеттері:
Теорема. Өзара тең векторларды қандай да бір параллель көшіру арқылы үйлестіруге (беттестіруге) болады және керісінше, параллель көшіру арқылы үйлесетін векторлар өзара тең болады.
Дәлелдеу.
Айталық,
және
 векторлары тең болсын. Онда анықтама
бойынша
векторлары тең болсын. Онда анықтама
бойынша
 және
және
 болады. Яғни
болады. Яғни
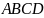 төртбұрышының АВ және
төртбұрышының АВ және
 қабырғалары параллель және ұзындықтары
тең болғандықтан, бұл төртбұрыш –
параллелограмм. Олай болса,
қабырғалары параллель және ұзындықтары
тең болғандықтан, бұл төртбұрыш –
параллелограмм. Олай болса,
 ,
яғни
векторын
векторларына параллель көшіру А-ны
С-ға, ал В-ны
,
яғни
векторын
векторларына параллель көшіру А-ны
С-ға, ал В-ны
 нүктесіне көшіреді.
нүктесіне көшіреді.
Керісінше,
векторын параллель көшіру арқылы
векторларына үйлестіруі мүмкін болсын.
Мұнда А нүктесі С-ға, ал В нүктесі
 ға көшетін болсын. Онда параллель
көшірудің қасиеттері бойынша
ға көшетін болсын. Онда параллель
көшірудің қасиеттері бойынша
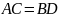 және
және
 болады, яғни
болады, яғни
 параллелограмм. Олай болса,
және
.
Ал параллель көшіру кезінде
және
векторларының басы басына, ұшы ұшына
көшетін болғандықтан,
болады. Яғни
параллелограмм. Олай болса,
және
.
Ал параллель көшіру кезінде
және
векторларының басы басына, ұшы ұшына
көшетін болғандықтан,
болады. Яғни
 .
Осы теоремадан параллеь көшірулер
арқылы үйлесетін векторларды тең деп
атауымызға болатынын көреміз. Егер
және
векторлары бір түзудің бойында орналасқан
болса, онда бұл теореманың дәлелдеуі
өте күрделі болмайды (бұл жағдайды өз
беттеріңше қарастырыңдар).
.
Осы теоремадан параллеь көшірулер
арқылы үйлесетін векторларды тең деп
атауымызға болатынын көреміз. Егер
және
векторлары бір түзудің бойында орналасқан
болса, онда бұл теореманың дәлелдеуі
өте күрделі болмайды (бұл жағдайды өз
беттеріңше қарастырыңдар).
Салдар
1.
Егер
 болса, онда
болса, онда
 болады (12,
13-сурет).
болады (12,
13-сурет).


(12-сурет). (13-сурет).
Егер А нүктесі векторының басы болса, онда векторын А нүктесінен бастап салынған деп есептейміз (14-сурет).

(14-сурет).
Салдар 2. Кез келген А нүктесінен бастап векторына тең бір ғана вектор салуға болады.
Шынында да, векторының бас нүктесін А нүктесіне көшіретін тек бір ғана параллель көшіру табылады. Онда бұл параллель көшіру арқылы алынатын векторының бейнесі де жалғыз және бұл бейненің векторына тең болатыны теоремадан шығады.
Осы айтылғандардан, әрбір вектор белгілі бір параллель көшіруді анықтайтындығын және керісінше, кез келген параллель көшіру белгілі бір вектор арқылы анықталатынын көреміз.
