1 Вектор

1.1 Вектор ұғымы.

Біздерге әр түрлі шамалар белгілі. Мысалы, ұзындық, аудан, көлем, масса және т.с.с. шамалар (белгілі өлшем бірліктеріне) өзлерінің сан мәндерімен толық анықталады. Мұндай шамаларды скаляр шамалар немесе жай ғана скаляр деп атаймыз.

Ал көптеген физикалықшамалар, мысалы, күш, материалдық дененің қозғалысы, жылдамдығы және т.с.с. шамалар тек өзінің сан мәндерімен ғана емес, кеңістіктегі бағыттарымен де сипатталады. Мұндай шамаларды векторлық шамалар немесе жай ғана вектор деп атайды. Мысалы, қандай да бір денеге белгілі бір күшпен әсер ететін болсақ, онда физика курсында бұл күшті «бағытталған кесіндімен» бейнелейді (1-сурет). Суретке 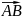вектор – тілше түрінде салынады.

(1-сурет).

Мұнда кесіндінің ұзындығы күштің сан мәніне сәйкес келсе, онда стрелка күштің әсерлік бағытын білдіреді.

Осы сияқты, геометриялық вектор ұғымын енгізуге болады. Физикамен салыстырғанда геометриялық векторлардың нақты табиғаты қарастырылмайды (яғни векторлардың белгілі бір күшті, жалдамдықты, қозғалысты және т.с.с физикалық немесе өзге шамаларды бейнелейтіндігі ескерілмейді). Геометриялық векторлар жай «бағытталған кесінді» ретінде қарастырылады.

Мәселен, әрбір кесіндінің екі ұшы болатынын жақсы білеміз. Егер осы ұштардың бірін бастапқы нүктесі немесе басы деп, ал екіншісін – ұшы деп алсақ, онда бұл кесінді бағытталған кесіндіге айналады. Төмендегі суретте бағытталған кесіндінің ұшы стрелкамен бейнеленген (2-сурет).

(2-сурет).

Әрине, кез келген кесіндіден (басы мен ұшын таңдап алуымызға байланысты) екі түрлі бағытталған кесінді алуымызға болады. Енді геометриялық векторларды анықтайық.

Анықтама 1. Кез келген бағытталған кесіндіні вектор деп атайды.

АВ кесіндідегі А – бас нүктесі, ал В – ұшы деп есептегендегі шығатын векторды арқылы белгілейді. Мысалы, жоғарыдағы суретте және векторлары бейнеленген. Сонымен, егер векторы берілсе, онда оның А нүктесі – оның басы, ал В – ұшы болады. Ал векторында керісінше, В – басы, А – ұшы болады. Векторларды көбінесе стрелкасы бар кіші латын әріптерімен де белгілейді: және т.б. (3-сурет).

(3-сурет).

Жалпы геометрияда басы мен ұшы беттесетін векторды да қарастырады. Мұндай векторды нөлдік вектор деп атайды. Осы айтылғаннан жазықтықтағы кез келген нүктені нөлдік вектор ретінде қарастыруымызға болатыны шығады. Нөлдік векторды 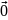арқылы белгілейміз.

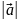АВ кесіндісінің ұзындығын векторының модулі деп атайды және оны арқылы белгілейді. Осы сияқты, векторының модулін (ұзындығын) арқылы белгілейміз. Мысалы, жоғарыдағы суреттерде бейнеленген векторлардың модульдері төмендегідей болады:

Егер АВ кесіндісі 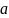түзуінде жататын болса, онда векторы да түзуінде жатады.

Егер екі вектор бір түзудің бойында немесе параллель түзулердің бойында жататын болса, онда бұл векторларды коллинеар (сызықтас) векторлар деп атайды. және векторларының коллинеарлылығын 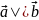арқылы белгілейді (4-сурет).

(4-сурет).

Егер және өзара перпендикуляр түзулердің бойында жататын болса, онда бұл векторларды өзара перпендикуляр (ортогональ) деп атаймыз және оны былай белгілейді (5-сурет).

(5-сурет).

Осы сияқты, егер векторы с түзуіне параллель (перпендикуляр) түзудің бойында жатса, онда векторы мен с түзуін параллель (перпендикуляр) деп атап, арқылы белгілейміз.

Егер коллинеар векторлардың бағыттары бірдей болса, онда бұл векторларды бағыттас векторлар деп атаймыз. және векторларының бағыттас болатындығын арқылы белгілейміз. Ал және векторлары колинеар және әр түрлі бағытталған болса, онда бұл векторларды қарама-қарсы бағытталған деп атап, оны былай белгілейді: .