8. Сложение гармонических колебаний, происходящих вдоль одной прямой. Сложение взаимно перпендикулярных колебаний.

Решение ряда задач значительно облегчается при использовании метода векторных диаграмм.

В основе метода лежит понятие вращающегося вектора.

x₀

О x

Возьмем ось x и из точки О отложим вектор x₀ под углом к оси x. Если привести вектор во вращение с угловой скоростью , то проекция конца этого вектора на ось x будет перемещаться по оси x в пределах от до , при этом координата будет изменяться по закону . Проекция конца вектора на ось будет совершать гармоническое колебание с амплитудой, равной длине вектора и частотой равной угловой скорости вращения .

Сложение колебаний, происходящих вдоль одной прямой.

Пусть точка совершает два колебания, происходящие вдоль одной прямой с одинаковой частотой, описываемых уравнениями:

Y

A

A₂

A ₁

X

x₂ x₁

Представив оба колебания в виде векторов и сложив их по правилу сложения векторов можно получить результирующее колебание. Это вектор, проекция которого на ось X равна сумме проекций исходных колебаний. .

Запишем результирующее колебание в виде

Из рисунка и

Частные случаи сложения колебаний

1) , где n=0,1,2….

Тогда

A

A ₁

A₂

t

2) ; n=0,1,2… , тогда

A₂

t

-A₁

3) Частоты двух слагаемых колебаний не совпадают друг с другом, но мало отличаются

Тогда слагаемые колебания будут представлены так :

, а их сумма , где

.

Такие колебания называются биениями. Множитель измеряется гораздо медленнее, чем второй множитель. Так как , за время, в течение которого множитель совершает несколько колебаний, почти не изменяется.

Это даёт нам право рассматривать результирующее колебание как гармоническое частоты w, амплитуда которого медленно изменяется по некоторому закону. Такие колебания называются пульсациями.

Сложение взаимно перпендикулярных колебаний

Допустим, что материальная точка будет совершать колебания в двух взаимно перпендикулярных направлениях. Если возбудить оба эти колебания, то точка будет двигаться по некоторой траектории, вид которой зависит от разности фаз складываемых колебаний. Пусть колебания заданы уравнениями:

(2), которые являются координатами движущейся точки, заданными в параметрической форме. Исключив из этих уравнений параметр t, получим уравнение траектории точки. Сделаем некоторые математические преобразования: , , , .

Развернём cos в уравнение (2) по формуле для косинуса суммы:

, подставим вместо и их значения, получим , после преобразования получим :

. Это уравнение эллипса.

Это уравнение представляет собой общее уравнение траектории материальной точки, совершающей два взаимно перпендикулярных колебания.

Рассмотрим частные случаи:

1) , , тогда , - это прямая проходящая через начало координат.

Y

X

2) - это эллипс, если a=b ,то это окружность.

Y

X

3) Если частоты колебаний не совпадают, то траектория имеет вид довольно сложных кривых, называемых фигурными Лиссану . Например

Y Y Y

X X X

При , траектории будут иметь вид (см.рис).

5. 1 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ

Колебаниями в физике не только называют периодические или почти периодические движения тел, когда колеблющееся тело многократно повторяет одно и то же движение туда и обратно около определенного положения, а придают этому понятию более широкий смысл. Под колебаниями понимают всякий периодический или приблизительно периодический процесс, в котором значение той или иной физической величины повторяется точно или приблизительно точно через равные или приблизительно равные промежутки времени.

Колебаться, или осциллировать, может груз на конце пружины, маятник, струны гитары или фортепиано, напряжение между обкладками конденсатора в контуре радиоприемника; колеблются атомы в молекулах, в твердом теле атомы совершают колебания относительно своих фиксированных положений в кристаллической решетке. Пауки обнаруживают попавшую в их сети добычу по дрожанию паутины, дома и мосты дрожат при проезде тяжелых грузовиков. Почти все материальные предметы колеблются после того, как на них подействует импульс силы.

В зависимости от характера воздействия на колеблющуюся систему различают свободные колебания, вынужденные колебания, автоколебания, параметрические колебания. Свободными, или собственными, называются такие колебания, которые совершает выведенная из положения равновесия или получившая толчок система, будучи предоставлена самой себе. Если колеблющаяся система подвергается в процессе колебаний воздействию внешней периодически меняющейся силы, то она совершает колебания, называемые вынужденными.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Говоря о колебаниях тела в механике, мы подразумеваем повторяющееся движение по одной и той же траектории. Простейшим примером периодического движения служат колебания груза на конце пружины (пружинный маятник) (рис. 7.1).

Если сдвинуть груз вправо, растягивая пружину, или влево, сжимая ее, то пружина действует на груз с силой, которая стремится вернуть его в положение равновесия; такую силу называют возвращающей. Для нашей системы возвращающая сила прямо пропорциональна расстоянию х, на которое сжимается или растягивается пружина ( ). Эта сила сообщает грузу ускорение, и груз приходит в положение равновесия. В положении равновесия сила, действующая на груз, уменьшается до нуля, а скорость его в этой точке максимальна. Возвратившись в устойчивое состояние, колебательная система не может сразу остановиться. В механических колебательных системах этому мешает инертность колеблющегося тела. Поэтому груз пройдет положение равновесия и будет двигаться далее, что приведет к сжатию пружины. Сила со стороны пружины в результате ее сжатия замедляет движение груза, и в некоторой точке его скорость будет равна нулю. Затем груз начинает двигаться в противоположном направлении и приходит в точку, откуда он начал движение. Затем весь этот процесс повторяется. Пружина, груз – пример колебательной системы. Расстояние х груза от положения равновесия до точки, в которой в данный момент времени находится груз, называют смещением.

Любая колебательная система, в которой возвращающая сила прямо пропорциональна смещению, взятому с противоположным знаком (например, упругая сила ), совершает гармонические колебания. Такую силу называют квазиупругой, а саму систему часто называют гармоническим осциллятором.

Рассмотрим уравнение, описывающее колебания, совершаемые системой в направлении оси X в отсутствие сил трения. Для этого воспользуемся вторым законом Ньютона . Ускорение , а так как , то ускорение можно получить, если два раза взять производную от координаты по времени. Тогда . Так в математике обозначается вторая производная. Теперь уравнение движения осциллятора можно записать в виде:

.

Введем обозначение , тогда уравнение запишется в следующем виде:

,

здесь – ускорение движущейся точки.

Поскольку , – величина, зависящая от свойств системы, совершающей колебания. Решение этого уравнения имеет вид:

(7.1)

где и – произвольные постоянные, которые определяются из начальных условий. В качестве таковых можно, например, взять значение отклонения и скорости в момент времени . В справедливости (7.1) можно убедиться на простом опыте. Если к колеблющемуся грузу прикрепить карандаш и протягивать под ним с постоянной скоростью лист бумаги, то карандаш вычертит синусоиду.

Таким образом, смещение изменяется со временем по закону косинуса или синуса. Движение механической системы, находящейся под действием квазиупругой силы, представляет собой гармоническое движение.

На рис. 7.2 приведен график зависимости смещения частицы от времени. По горизонтальной оси отложено время , по вертикальной – смещение x. Так как косинус изменяется от -1 до +1, значения лежат в пределах от до . Величина наибольшего отклонения системы от положения равновесия называется амплитудой колебания. Амплитуда – постоянная положительная величина. Величина , стоящая под знаком косинуса, называется фазой колебания. Постоянная представляет собой значение фазы в момент и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета времени.

Поскольку косинус – периодическая функция с периодом , различные состояния частицы, совершающей гармонические колебания, повторяются через такой промежуток времени T, за который фаза колебания получает приращение . Этот промежуток времени называется периодом колебания. Его можно определить из условия:

,

отсюда

.

Число колебаний в единицу времени называется частотой колебаний. Очевидно, что частота связана с периодом колебаний соотношением

.

Из определения периода следует, что . Величину называют круговой или циклической частотой. Так как она зависит от свойств самой колеблющейся системы, то ее часто называют собственной частотой колебаний системы.

Примером системы, совершающей гармонические колебания, является математический маятник. Математический маятник – это тело, подвешенное на невесомой и нерастяжимой нити, находящееся в поле тяжести Земли. Математический маятник представляет идеализированную модель, правильно описывающую реальный маятник лишь при определенных условиях. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.

Колебательную систему в данном случае образуют нить, присоединенное к ней тело и Земля, без которой эта система не могла бы служить маятником. При колебаниях математического маятника периодически изменяется угол отклонения маятника от положения равновесия. Период свободных гармонических колебаний математического маятника равен

,

где – длина нити, g – ускорение свободного падения. Таким образом, период свободных колебаний математического маятника не зависит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.

ЭНЕРГИЯ ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА

Во время колебательных процессов происходит периодическое превращение потенциальной энергии системы в кинетическую. Например, отклонив математический маятник в сторону и, следовательно, подняв его на высоту h, ему сообщают потенциальную энергию . Она полностью переходит в кинетическую энергию движения , когда груз проходит положение равновесия и скорость его максимальна. При колебаниях пружинного маятника кинетическая энергия движения груза переходит в потенциальную энергию деформированной системы. Величина полной энергии колеблющейся системы в любой момент времени равна сумме ее кинетической и потенциальной энергии:

или

.

(7.2)

 

Поскольку скорость – это первая производная от координаты по времени, то

.

Учитывая, что и подставив выражения для и , получим:

.

То есть полная энергия системы, совершающей колебания, пропорциональна ее массе, квадрату амплитуды и квадрату собственной частоты. Так как силы, действующие на колеблющуюся частицу, являются консервативными, то ее механическая энергия остается постоянной. В процессе же колебаний происходит превращение кинетической энергии в потенциальную и обратно.

На рис. 7.3 приведен график зависимости потенциальной энергии от координаты частицы. С ростом x уменьшается кинетическая энергия и увеличивается потенциальная. Максимального значение потенциальная энергия достигает в поворотных точках , при этом кинетическая энергия равна нулю. Среднее за период значение кинетической энергии равно среднему за период значению потенциальной энергии.

Скорость, ускорение и энергия колеблющегося тела.

Вернемся к формулам для смещения x, скорости v и ускорения a гармонического колебательного процесса.

Пусть имеем тело массы «m», которое совершает под действием квазиупругой силы колебания по закону:

, тогда

.

.

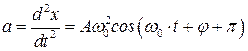Видно, что скорость и ускорение также изменяются по гармоническому закону (графики приводились ранее) с периодом колебаний равным T. Из сравнения формул видно, что скорости v опережает смещение по фазе на . Это означает, что если x=0, то v тела имеет максимальное значение .

Для ускорения зависимость иная. В каждый момент времени ускорение пропорционально смещению и находится с ним в противофазе. Это означает, что когда x=x_max, то ускорение тоже максимально, но отрицательно, т.е. при x=x_max, (графики приведены ранее).

Квазиупругая сила, под действием которой происходит колебательное движение, является консервативной. Поэтому полная энергия гармонического колебательного движения должна оставаться постоянной. В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно (силами сопротивления пренебрегаем). Причем в моменты наибольшего отклонения о положения равновесия , причем ; при прохождении положения равновесия , причем . Так как , то .

Определим, как со временем изменяется Е_к и U_п для гармонического колебания . Имеем

(8.4)

(8.5)

Т.к. , то имеем

,

т.е. как и должно было быть, т.к. квазиупругая сила – консервативная сила.

Используя формулы тригонометрии, можно получить выражения для

(8.6)

(8.7)

Здесь E – полная энергия системы. Из формул видно, что Е_к и U_п изменяются с частотой 2w₀, т.е. с частотой вдвое превышающей частоту гармонического колебания. Среднее значение квадрата sin и квадрата cos равно 1/2. Следовательно, среднее значение E_к совпадает со средним значением U_п и равно E/2.

ЛЕКЦИЯ 11

Гармонический осциллятор.

Систему, описываемую уравнением , где , будем называть гармоническим осциллятором. Решение этого уравнения, как известно, имеет вид:

.

Следовательно, гармонический осциллятор представляет собой систему, которая совершает гармонические колебания около положения равновесия.

Для гармонического осциллятора справедливы все результаты, полученные ранее для гармонического колебания.

Рассмотрим и обсудим ещё дополнительно к ним два вопроса.

Найдем импульс гармонического осциллятора. Продифференцируем выражение по t и, умножив полученный результат на массу осциллятора, получим:

. (8.8)

В каждом положении, характеризуемом отклонением “x”, осциллятор имеет некоторое значение ”p”. Чтобы найти ”p” как функцию ”x”, нужно исключить ”t” из написанных для ”p” и ”x” уравнений, Представим эти уравнения в виде:

(8.9)

Возведя эти выражения в квадрат и складывая, получим:

. (8.10)

Нарисуем график, показывающий зависимость ”p” импульса гармонического осциллятора от отклонения ”x” (рис. 8.6). Координатную плоскость (”p”, ”x”) принято называть фазовой плоскостью, а соответствующий график – фазовой траекторией. Фазовая траектория гармонического осциллятора представляет собой эллипс с полуосями “A” и ”A·m·w₀”. Каждая точка фазовой траектории изображает состояние осциллятора для некоторого момента времени (т.е. его отклонение и импульс). С течением времени точка, изображающая состояние, перемещается по фазовой траектории, совершая за период колебания полный обход. Причем это перемещение совершается по часовой стрелке [а именно, если в некоторый момент времени t¢ x=A, p=0, то в следующий момент времени ”x” будет уменьшаться, а ”p” принимать все возрастающие по модулю отрицательные значения, т.е. движение изобразительной точки (т.е. точки изображающей состояние) будет происходить по часовой стрелке].

Найдем теперь площадь эллипса . Или

.

Здесь , где n₀ – собственная частота осциллятора, являющаяся для данного осциллятора величиной постоянной.

Следовательно, . Откуда

. (8.11)

Таким образом, полная энергия гармонического осциллятора пропорциональна площади эллипса, причем коэффициентом пропорциональности служит собственная частота осциллятора.

8.6. Малые колебания системы вблизи положения равновесия.

Рассмотрим произвольную механическую систему, положение которой может быть задано с помощью одной величины “x”. Величиной ”x”, определяющей положение системы может быть угол, отсчитываемый от некоторой плоскости или расстояние, отсчитываемое вдоль заданной кривой.

Потенциальная энергия такой системы будет функцией одной переменной ”x”: E_p=E_p(x).

Выберем начало отсчета таким образом, чтобы в положении равновесия x=0. Тогда функция E_p(x) будет иметь минимум при x=0.

Далее разложим функцию E_p(x) в ряд по степеням “x”, причем ограничимся случаем малых колебаний, поэтому высшими степенями “x” можно пренебречь. По формуле Маклорена:

.

(ввиду малости “x” остальными членами пренебрегаем)

Так как E_p(x) при x=0 имеет минимум, то , а . Обозначим E_p(x) = b и , тогда .

Это выражение идентично с выражением для потенциальной энергии системы, в которой действует квазиупругая сила (константу “b” можно положить равной 0).

Сила, действующая на систему, может быть определена по формуле: 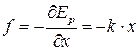. Получено с учетом, что работа совершается за счет убыли потенциальной энергии .

Итак, потенциальная энергия системы при малых отклонениях от положения равновесия оказывается квадратичной функцией смещения, а сила, действующая на систему, имеет вид квазиупругой силы. Следовательно, при малых отклонениях от положения равновесия любая механическая система будет совершать колебания, близкие к гармоническим.

8.7. Математический маятник.

ОПРЕДЕЛЕНИЕ: математическим маятником будем называть идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.

Отклонение маятника от положения равновесия будет характеризоваться углом j (рис. 8.7). При отклонении маятника от положения равновесия возникает вращательный момент , он имеет такое направление, что стремится вернуть маятник в положение равновесия, поэтому моменту M и угловому смещению j нужно приписать разные знаки.

Следовательно,

. (8.12)

Напишем теперь для маятника уравнение динамики вращательного движения (учитывая, что b – угловое ускорение равно , а ).

Рассмотрим малые колебания ( ) и введем величину , тогда получим

Решением этого уравнения будет функция

Следовательно, при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону.

Как следует из формулы , частота колебаний математического маятника зависит только от его длины и величины “g” и не зависит от массы маятника. Учитывая, что получим

. (8.13)

Физический маятник.

ОПРЕДЕЛЕНИЕ: Физическим маятником будем называть твердое тело, способное совершать колебания вокруг неподвижной оси, не проходящей (не совпадающей) через его центр инерции.

При отклонении маятника от положения равновесия на угол j возникает вращательный момент, стремящийся вернуть маятник в положение равновесия (рис. 8.8).

Этот момент равен

,

где m – масса маятника; l – расстояние от точки подвеса «О» до центра инерции маятника «С».

Обозначим J – момент инерции маятника относительно оси, проходящей через точку подвеса, тогда . В случае малых колебаний получим уравнение

,

где . Отсюда следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника.

Период колебаний физического маятника будет определяться выражением:

. (8.14)

Сопоставляя это выражение с периодом колебаний математического маятника получаем, что математический маятник с длиной будет иметь такой период колебаний, как и данный физический маятник. Эта величина называется приведенной длиной физического маятника.

ОПРЕДЕЛЕНИЕ: Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

ЛЕКЦИЯ 12

Затухающие колебания.

При выводе уравнения гармонических колебаний считалось, что колеблющаяся точка находится под действием только квазиупругой силы. Во всякой реальной колебательной системе всегда имеются силы сопротивления (например, это может быть сила трения в точке подвеса, сопротивление среды, в которой совершаются колебания). Действие этих сил приводит к тому, что энергия колеблющейся системы (или точки) будет непрерывно убывать. Эта убыль энергии будет равна работе против сил трения и сопротивления. Т.к. полная энергия колебаний пропорциональна квадрату амплитуды , то наличие сил трения и сопротивления приведет и к непрерывному убыванию амплитуды колебаний. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать (и носят название затухающих).

Итак, затухание колебаний в любой колебательной системе (механической, электрической и т.п.) обусловлено потерями энергии в этой системе. Потери энергии колебаний в механических колебательных системах происходят из-за трения (внешнего и внутреннего) и излучения упругих волн в окружающую среду; в электрических – из-за наличия активного сопротивления проводников и т.п.

Рассмотрим свободные (или собственные) колебания. Это значит, что система, будучи выведена из положения равновесия в результате внешнего воздействия, в дальнейшем предоставлена самой себе и находится под воздействием только квазиупругой силы F=-kx и силы сопротивления среды, значит она будет совершать затухающие колебания вдоль оси “x”.

Ограничимся рассмотрением малых колебаний, тогда и скорость (v) системы будет малой, а при небольших скоростях сила сопротивления пропорциональна скорости:

,

где r – коэффициент сопротивления среды. Знак минус (“-”), т.к. и имеют противоположные направления.

Под действием сил F и f тело приобретает ускорение “a”, и для колеблющегося тела уравнение II-закона Ньютона имеет вид:

или .

Обозначим ; , тогда

(8.15)

– дифференциальное уравнение затухающих колебаний

Здесь w₀ – та частота, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды (т.е. при r = 0). Эта частота называется собственной частотой колебаний системы. b – коэффициент затухания колебаний (зависит от свойств данной системы и среды).

Наличие сопротивления среды приводит к тому, что амплитуда колебаний со временем будет уменьшаться. Поэтому будем искать решение уравнения (8.15) в виде:

где a(t) – некоторая функция времени.

Продифференцируем это выражение по времени и найдем и :

После подстановки этих выражений в уравнение (8.15) и несложных преобразований придем к следующему соотношению:

.

Для того чтобы уравнение удовлетворялось при любых значения “t”, необходимо равенство нулю коэффициентов при “sin” и ”cos”. Т.е. приходим к двум следующим уравнениям:

	(8.16)
	(8.17)

Первое уравнение представим в виде:

или .

После интегрирования получим , где – постоянная интегрирования. После потенцирования найденного выражения получим . Видно, что , а . Подставим эти значения в (8.17), получим

.

Отсюда .

При w₀ > b, величина w будет вещественной и тогда решение дифференциального уравнения может быть представлено в виде

.

Таким образом, при не слишком большом затухании колебания описываются функцией

.

График этой функции показан на рисунке 8.9. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Движение такой системы можно рассматривать как гармоническое колебание с частотой w и амплитудой, изменяющееся по закону Верхняя из пунктирных кривых дает график функции a(t), причем величина a₀ представляет собой амплитуду в начальный момент времени. Начальное смещение x₀ зависит, кроме a₀, также от начальной фазы a: .

Скорость затухания колебаний определяется величиной , которую называют коэффициентом затухания. Найдем время t, за которое амплитуда колебаний уменьшается в “e” раз. По определению .

Следовательно, коэффициент затухания равен обратной величине того промежутка времени, за который амплитуда колебаний уменьшается в “e” раз.

С учетом того, что , а период затухающих колебаний можно определить как

.

При незначительном сопротивлении среды период колебаний практически равен . С ростом коэффициента затухания период колебаний увеличивается.

Для характеристики колебательной системы (а именно: убывания амплитуды колебаний в зависимости от числа колебаний) вводится величина, называемая логарифмическим декрементом затухания (l).

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период равно

– это отношение называется декрементом затухания, а его логарифм – логарифмическим декрементом затухания.

, т.е. . Т.к. , то . Отсюда следует, что логарифмический декремент затухания l зависит от свойств данной системы и среды.

Выразим и запишем закон убывания амплитуды в виде . За время t, за которое амплитуда колебаний уменьшится в “e” раз система совершит колебаний. Из условия получаем . Поэтому .

Следовательно, логарифмический декремент затухания равен обратной величине числа колебаний, совершаемых системой за то время, за которое амплитуда уменьшается в “e” раз (l – безразмерная величина).

Для характеристики колебательной системы также часто употребляется величина , называемая добротностью колебательной системы. Как видно из определения, добротность пропорциональна числу колебаний N, совершаемых системой за время t, за которое амплитуда колебаний убывает в “e” раз.

Как известно, энергия колеблющейся системы пропорциональна квадрату амплитуды. Поэтому энергия системы при затухающих колебаниях убывает со временем по закону

,

где E₀ – значение энергии при t = 0.

Продифференцировав это выражение по “t”, получим скорость возрастания энергии

.

Изменив знак на обратный, найдем скорость убывания энергии: .

Если энергия мало изменяется за время равное периоду колебаний, то убыль энергии за период будет равна .

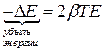С учетом и получим , т.е. при слабом затухании колебаний добротность с точностью до множителя 2p равна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний.

Из формулы для периода колебаний следует, что с ростом коэффициента затухания период колебаний увеличивается, а при b = w₀ период колебаний обращается в бесконечность, т. е., движение перестает быть периодическим.

И последнее, математический анализ показывает, что при условии движение носит апериодический (непериодический) характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.

План:

Введение

• 1 Свободные колебания

  • 1.1 Консервативный гармонический осциллятор

    • 1.1.1 Простое гармоническое движение

      • 1.1.1.1 Динамика простого гармонического движения

      • 1.1.1.2 Энергия простого гармонического движения

      • 1.1.1.3 Примеры

        • 1.1.1.3.1 Груз на пружине

        • 1.1.1.3.2 Универсальное движение по окружности

        • 1.1.1.3.3 Груз как простой маятник

  • 1.2 Затухающий гармонический осциллятор

• 2 Вынужденные колебания

Литература Примечания

Введение

Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы , пропорциональной смещению (согласно закону Гука):

где k — положительная константа, описывающая жёсткость системы.

Если  — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами смещения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь).