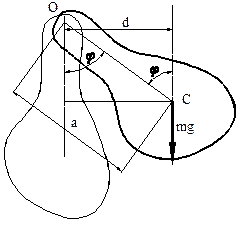Скорость и ускорение при гармоническом колебании. Энергия гармонического осциллятора.

Скорость и ускорение при гармоническом колебании.

=

- амплитудное значение скорости

Скорость опережает смещение по фазе на .

=

Сдвиг фаз между и равен , они колеблются в противофазах.

Сила.

Силы, которые подчиняются закону упругой силы, но по природе своей не являются упругими называются квазиупругими.

Гармонические колебания – это колебания, которые происходят под действием квазиупругой силы, то есть силы, пропорциональной смещению.

6. Энергия гармонического осциллятора.

(кинетическая Энергия, Т + потенциальная энергия, П = полной энергии, Е).

Пусть

.

Тогда

=

=

= + = .

- полная энергия механического осциллятора не зависит от и пропорциональна . Механический осциллятор есть консервативная система, так как .

Выводы:

Кинетическая и потенциальная энергии по отдельности зависят от времени.

Максимальная кинетическая энергия равна максимальной потенциальной энергии и равна полной энергии.

Средняя кинетическая энергия равна средней потенциальной энергии и равна половине полной энергии.

Полная энергия не зависит от времени и пропорциональна квадрату амплитуды.

Лекция 8. Сложение колебаний.

Сложение колебаний – задача сложная и часто пользуются искусственными приемами для ее решения. Представим гармоническое колебание в виде вектора амплитуды.

Модуль вектора равен амплитуде колебаний. Откладывают под углом . Проекция вращают равномерно с угловой скоростью, равной круговой частоте колебаний

В момент проекция на ось вектора равна . Получили уравнение гармонических колебаний. Итак, всякому гармоническому колебанию можно сопоставить вектор амплитуды, вращающийся с угловой скоростью , равной круговой частоте колебания. Тогда проекция этого вектора на ось совершает гармонические колебания. Физического смысла здесь нет, но решение задачи облегчается.

1. Сложение гармонических колебаний одного направления и одной частоты.

.

Изобразим их графически:

=

Векторы и вращаем с . Поскольку частоты равны, то параллелограмм, не деформируясь, вращается с той же частотой. Длина не меняется. Его проекция совершает гармонические колебания.

, но .

То есть результирующее колебание гармоническое, имеет ту же частоту, что и слагаемые колебания. Амплитуду находим из начальных условий по формуле

,

2. Биения.

Рассмотрим сложение колебаний одинаковой амплитуды и близких частот , , . Решение задачи усложняется.

.

Если изобразить эти колебания с помощью вектора амплитуды, то они вращаются с разными угловыми скоростями, и всегда будет момент, когда . Фазы в этот момент принимают за нуль. Тогда

.

= =

= .

=

- уравнение биений. Первый множитель медленно меняется, второй – быстро. Уравнение можно представить в виде

Сравним с уравнением гармонических колебаний

.

Уравнение биений – негармоническое, но меняется медленно, так как мало.

.

Поэтому биения – приблизительно гармонические колебания с медленно меняющейся амплитудой, может быть больше и меньше нуля.

- амплитуда. Для гармонических колебаний

- мало, велико. - частота биений.

Амплитуда ограничивает . (Проводим штрихами симметричную кривую внизу).Частота . . Получили биения – усиление и ослабление колебаний.

Метод биений широко применяется на практике. Основан на сравнении искомой частоты с частотой эталона. Метод биений – это один из наиболее точных методов измерения частот, емкостей, индуктивностей. Применяют для настройки музыкальных инструментов.

Скорость и ускорение при гармоническом колебании

Задача о математическом маятнике.

Задача о физическом маятнике.

Задача о колебании груза на пружине.

Свободные гармонические колебания. Гармонический осциллятор.

Периодические колебания называются гармоническими, если они описываются законами sin или cos. Любая колеблющаяся система, любой физический процесс, описываемый законами sin или cos называется гармоническим осциллятором или просто осциллятором.

Примеры:

Дифференциальное уравнение свободных гармонических колебаний

Первоначально система находится в равновесии

Систему вывели из положения равновесия на . Деформация будет .

По второму закону Ньютона Преобразуем выражение к виду . Обозначим . Получим . Это линейное однородное дифференциальное уравнение второго порядка. Оно описывает колебания

груза на пружине. Решение его есть

,

,

что проверяется непосредственной подстановкой.

Физический маятник – это любое твердое тело, колеблющееся относительно оси, не проходящей через его центр.

Если ось проходит через центр тяжести, то тело находится в состоянии безразличного равновесия и колебаться не будет. Ось вращения проходит через точку О. Центр тяжести

Находится в точке С. ОС =а, - угол поворота. В точке С приложена сила тяжести, в точке О – сила реакции, она направлена вертикально вверх. Поскольку она проходит через ось вращения, то ее момент равен нулю. Вращающий момент создает сила . . Этот вращающий момент стремится вернуть тело к положению равновесия.

По второму закону Ньютона

Знак (-) означает, что тело стремится в равновесие. Теперь

.

Это нелинейное дифференциальное уравнение, в него входит . Поэтому в общем случае физический маятник колеблется не по гармоническому закону. Рассмотрим частный случай, когда мало и = . Тогда

, , , .

Уравнение

- это однородное линейное дифференциальное уравнение второго порядка. Оно описывает гармонические колебания.

Это частный случай физического маятника. Математическим маятником называется материальная точка, подвешенная на нерастяжимой нити. (Груз, подвешенный на нерастяжимой длинной нити, размерами груза по сравнению с длиной нити можно пренебречь): - формула Гюйгенса.

При многих расчетах удобно представить формулу периода физического маятника как математического. Вводят приведенную длину физического маятника

.

Тогда

.

Приведенной длиной физического маятника называется длина такого маятника, период колебания которого равен периоду колебания данного физического маятника. Экспериментально, введя , определяют любого маятника. Подбирают длину математического маятника, чтобы . Тогда . Определяя и , находят .

Продолжим рассмотрение гармонических колебаний.

1) - смещение колеблющегося тела от положения равновесия в любой момент времени (или значение осциллирующего параметра в момент времени ).

2) - амплитуда – максимальное отклонение от положения равновесия, или максимальное значение осциллирующего параметра, всегда.

3) - фаза колебания, измеряется в радианах, фаза определяет значение осциллирующего параметра в любой момент времени. - начальная фаза в нулевой момент времени.

4) - собственная циклическая (круговая) частота.

Связь и .

Рассмотрим значение осциллирующего параметра в моменты и , где - период. По определению они должны быть одинаковы.

,

,

= .

- наименьший промежуток времени, через который смещение повторилось. Поэтому аргументы могут отличаться на .

, ,

, , , ,

- число колебаний за 1 с, - число колебаний за с.

=

- амплитудное значение скорости

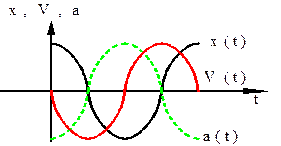
Скорость опережает смещение по фазе на .

=

Сдвиг фаз между и равен , они колеблются в противофазах.

«МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ» План лекции

1. Колебательное движение. Гармоническое колебание.

2. Скорость и ускорение гармонического колебания.

3. Энергия гармонического колебательного движения.

4. Свободные колебания. Гармонический осциллятор.

5. Пружинный, математический и физический маятники.

6. Вынужденные колебания. Резонанс. Автоколебания.

7. Примеры проявления резонансных явлений в живых организмах.

8. Сложение гармонических колебаний, происходящих вдоль одной прямой. Сложение

1. Колебательное движение. Гармоническое колебание. Вывод уравнения гармонического колебания

Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения.

Колебаниями называется процессы, отличающиеся той или иной степенью повторяемости (качели, ветка дерева, фазы луны, морские приливы и отливы, пульсовая волна, сердце, гортань…). В технике и окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.

Колебания широко распространены в природе и технике. Колебательные процессы лежат в основе таких отраслей техники как электротехника, радиотехника и.т.д).

Во многих случаях колебания играют негативную роль (вибрации крыльев самолёта, корпусов судов, зданий и сооружений из за резонанса с работающим там оборудованием), что необходимо учитывать при их изготовлении.

В зависимости от физической природы колебания бывают механические и электромагнитные. Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник.

В зависимости от характера воздействия на колеблющуюся систему, различают: свободные, (собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.

1. Свободные колебания, совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. (Колебания груза на пружине или колебания маятника являются свободными колебаниями.).

2. Вынужденные - система подвергается воздействию внешней, периодически изменяющийся силы (колебание моста при прохождении солдат, идущих в ногу).

3. Автоколебания - система сама управляет внешним воздействием (маятник часов получает толчки в момент прохождения её через среднее положение).

4. Параметрические колебания - происходит периодическое изменение какого- либо параметра системы за счет внешнего воздействия (например длины нити математического маятника).

Простейшими являются гармонические колебания – происходящие по закону sin и cos.

Этот вид колебаний важен по двум причинам:

1. колебания в природе и технике часто близки к гармоническому.

2. иные периодические процессы могут быть представлены как наложение нескольких гармонических колебаний.

Выведем уравнение гармонического колебания при помощи установки, состоящей из экрана и вращающегося диска с закреплённым на нём непрозрачным шариком.

А w

M

x x А

свет

О o

- А

Пусть материальная точка М движется против часовой стрелки по окружности радиусом А. Тогда её проекция на экране совершает периодические колебания около положения равновесия в пределах от А до -А .

Выразим величину смещения xв любой момент времени:

- уравнение гармонического колебания.

Так как диск вращается с угловой скоростью w, то . Подставим значение в уравнение гармонического колебания:

- уравнение гармонического колебания.

Если диск совершает полный оборот ;

Основные характеристики гармонического колебания:

1x- смещение- отклонение от положения равновесия в данный момент времени (может быть >0 и <0)/

2A – амплитуда - максимальное отклонение от положения равновесия.

3T- период - совершения одного полного колебания.

4wt- фаза колебания - характеризует состояние колебательной системы в любой заданный момент времени.

5v- частота- число колебаний в единицу времени.

Если к началу наблюдения фаза имела некоторое начальное значение , то уравнение запишется:

- гармоническое колебание с начальной фазой.