Федеральное агентство связи

Сибирский Государственный Университет Телекоммуникаций и Информатики

Межрегиональный центр переподготовки специалистов

Контрольная работа

По дисциплине: Метрология, стандартизация, сертификация

Выполнил: _____________ Группа: ________________

Вариант: _______________

Новосибирск, 2017 г.

Задача № 1

Для определения расстояния до места повреждения кабельной линии связи был использован импульсный рефлектометр. С его помощью получено результатов однократных измерений (результатов наблюдений) расстояния до места повреждения.

Считая, что случайная составляющая погрешности рефлектометра распределена по нормальному закону, определить:

1. Результат измерения с многократными наблюдениями расстояния до места повреждения кабеля .

2. Оценку среднего квадратического отклонения (СКО) погрешности результата наблюдений (стандартную неопределенность единичного измерения) ;

3. Границы максимальной неопределенность случайной составляющей погрешности результата наблюдений ;

4. Оценку среднего квадратического отклонения погрешности случайной составляющей результата измерения (стандартную неопределенность результата измерения) ;

5. Границы доверительного интервала (расширенную неопределенность) для результата измерения расстояния до места повреждения при заданной доверительной вероятности ;

6. Записать результат измерения расстояния до места повреждения в соответствии с нормативными документами.

7. Систематическую составляющую погрешности измерения рефлектометра , если после обнаружения места повреждения было установлено, что действительное расстояние до него составляло метров. Сравните ее с доверительным интервалом случайной составляющей погрешности результата измерения, и сделать вывод;

8. Предложить способ уменьшения оценки СКО случайной составляющей погрешности результата измерения в раз.

: 5 – 10;

;

;

: 90 – 96;

.

Таблица 1.1 Номера наблюдений

	5	6		7		8		9		10
	275,81	273,50		276,65		275,81		273,28		275,30
	90	91	92		93		94		95		96
	275,28	274,31	274,99		274,09		273,24		276,75		274,73

Решение:

1. Результат измерения с многократными наблюдениями расстояния до места повреждения кабеля определяется по формуле ([1], ф.4.6):

Подставив значения, получаем:

Для удобства выполнения расчетов составим таблицу промежуточных вычислений (см. таблицу 1.2)

Таблица 1.2 Промежуточные вычисления

№ п/п	№ измерений
1	5	275,81	1,137692	1,294344
2	6	273,50	-1,172308	1,374305
3	7	276,65	1,977692	3,911267
4	8	275,81	1,137692	1,294344
5	9	273,28	-1,392308	1,938521
6	10	275,30	0,627692	0,393998
7	90	275,28	0,607692	0,369290
8	91	274,31	-0,362308	0,131267
9	92	271,99	-2,682308	7,194775
10	93	274,09	-0,582308	0,339082
11	94	273,24	-1,432308	2,051505
12	95	276,75	2,077692	4,316805
13	96	274,73	0,057692	0,003328
	–

2. Оценку среднего квадратического отклонения (СКО) погрешности результата наблюдений (стандартную неопределенность единичного измерения) найдем по формуле ([1], ф.4.23):

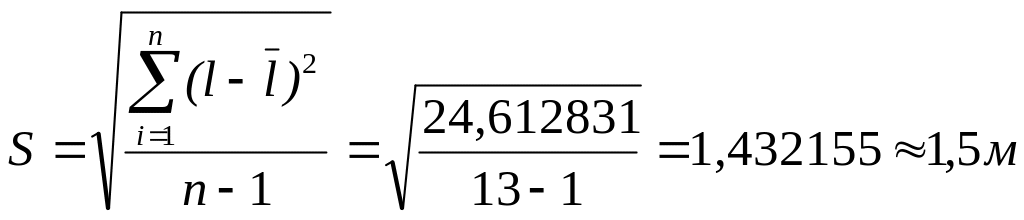
Определим погрешность округления:

_{Погрешность не превышает 5%, следовательно, округление верно.}

3. Границы максимальной неопределенность случайной составляющей погрешности результата наблюдений определяется по формуле ([1], стр.73):

Определим погрешность округления:

_{Погрешность не превышает 5%, следовательно, округление верно.}

4. Оценку среднего квадратического отклонения погрешности случайной составляющей результата измерения (стандартную неопределенность результата измерения) определим по формуле ([1], ф.4.28):

Определим погрешность округления:

_{Погрешность не превышает 5%, следовательно, округление верно.}

5. Границы доверительного интервала (расширенную неопределенность) для результата измерения расстояния до места повреждения при заданной доверительной вероятности определим по формуле ([1], стр.74):

− коэффициент Стьюдента, при заданной доверительной вероятности ( ) и числа наблюдений ([1], Приложение II, стр.413).

Определим погрешность округления:

Погрешность превышает допустимые 5%, следовательно, округляем в меньшую сторону до двух значащих цифр ( ).

6. Запишем результат измерения расстояния до места повреждения в соответствии с МИ 1317-2004.

, , , условия измерения нормальные.

7. Систематическую составляющую погрешности измерения рефлектометра можно определить, зная действительное значение расстояния . Воспользуемся формулой ([2], стр. 17):

, где

– действительное значение расстояния до места повреждения;

– результат измерения расстояния до места повреждения.

Определим погрешность округления:

_{Погрешность не превышает 5%, следовательно, округление верно.}

Найденное значение систематической составляющей погрешности измерения выходит за рамки доверительного интервала: 2,4 > 1,2. Следовательно, имеется систематическая погрешность.