Работа сил электростатического поля по перемещению заряда. Разность потенциалов и потенциал

Работа сил электростатического поля. Потенциал. Эквипотенциальные поверхности

На заряд q_пр помещённый в произвольную точку электростатического поля с напряжённостью Е, действует сила F= q_пр E. Если заряд не закреплён, то сила заставит его перемещаться и, значит, будет совершаться работа. Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда q_пр из точки а электрического поля в точку b на отрезке пути dℓ, по определению, равна

dA = Fdℓcosα

(α - угол между F и направлением движения) (рис.12.13).

Если работа совершается внешними силами, то dA< 0 , если силами поля, то dA > 0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении q_пр из точки a в точку b

(12.20)

Рисунок -12.13

( - кулоновская сила, действующая на пробный зарядq_пр в каждой точке поля с напряжённостью E).

Тогда работа

(12.21)

Перемещение совершается перпендикулярно вектору  , следовательноcosα =1, работа переноса пробного заряда q_пр от a к b равна

(12.22)

Работа сил электрического поля при перемещении заряда не зависит от формы пути, а зависит лишь от взаимного расположения начальной и конечной точек траектории.

Следовательно, электростатического поля точечного заряда является потенциальным , а электростатические силы – консервативными.

Это свойство потенциальных полей. Из него следует, что работа совершаемая в электрическом поле по замкнутому контуру, равна нулю:

(12.23)

Интеграл   называется циркуляцией вектора напряженности. Из обращения в нуль циркуляции вектора Е следует, что линии напряжённости электростатического поля не могут быть замкнутыми, они начинаются на положительных и кончаются на отрицательных зарядах.

Как известно, работа консервативных сил совершается за счёт убыли потенциальной энергии. Поэтому, работу сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд q_пр в начальной и конечной точках поля заряда q:

(12.24)

откуда следует, что потенциальная энергия заряда q_пр в поле заряда q равна

(12.25)

Для одноименных зарядов q_прq >0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноимённых зарядов q_прq < 0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Если поле создаётся системой n точечных зарядов q_1, q_2, …. q_n, то потенциальная энергия U заряда q_пр, находящегося в этом поле, равна сумме его потенциальных энергий U_i, создаваемых каждым из зарядов в отдельности:

(12.26)

Отношение  не зависят от зарядаq и является энергетической характеристикой электростатического поля.

Скалярная физическая величина, измеряемая отношением потенциальной энергии пробного заряда в электростатическом поле к величине этого заряда, называется потенциалом электростатического поля.

(12.27)

Потенциал поля, создаваемый точечным зарядом q, равен

(12.28)

Единица потенциала – вольт.

Работа, совершаемая силами электростатического поля при перемещении заряда q_пр из точки 1 в точку 2 может быть представлена как

(12.29)

т.е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках.

Разность потенциалов двух точек электростатического поля φ₁-φ₂ равна напряжению. Тогда

Отношение работы, совершаемой электростатическим полем при перемещении пробного заряда из одной точки поля в другую, к величине этого заряда называется напряжением между этими точками.

(12.30)

Графически электрическое поле можно изображать не только с помощью линий напряжённости, но и с помощью эквипотенциальных поверхностей.

Эквипотенциальные поверхности – совокупность точек, имеющих одинаковый потенциал. Из рисунка видно, что линии напряжённости (радиальные лучи) перпендикулярны эквипотенциальным линиям.

Эк випотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесчисленноемножество (рис.12.14). Однако их проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряжённость поля в разных точках. Там, где эти поверхности расположены гуще, напряжённость поля больше. Зная расположение эквипотенциальных линий (поверхностей), можно построить линии напряжённости или по известному расположению линий напряжённости можно построить эквипотенциальные поверхности.

§ 12.4 Связь напряжённости и потенциала

Электростатическое поле имеет две характеристики: силовую (напряжённость) и энергетическую (потенциал). Напряжённость и потенциал – различные характеристики одной и той же точки поля, следовательно, между ними должна быть связь.

Работа по перемещению единичного точечного положительного заряда из одной точки в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и х₁– х₂ = dx , равна qЕ_хdx. Та же работа равна q(φ₁ - φ₂ )= -dφq. Приравнивая оба выражения, можем записать

Е_хdx = -dφ

Повторив аналогичные рассуждения для осей у и z, можем найти вектор  :

где  - единичные векторы координатных осей х, у,z.

Из определения градиента следует, что

или  (12.31)

т.е. напряжённость поля Е равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряжённости Е поля направлен в сторону убывания потенциала.

Установленная связь между напряжённостью и потенциалом позволяет по известной напряжённости поля найти разность потенциалов между двумя произвольными точками этого поля.

• Поле равномерно заряженной сферы радиусом R

Напряжённость поля вне сферы определяется по формуле

(r >R)

Разность потенциалов между точками r₁ и r₂ (r₁>R; r₂ >R ) определим, используя соотношение

Потенциал сферы получим, если r₁= R, r₂ → ∞:

• Поле равномерно заряженного бесконечно длинного цилиндра

Напряжённость поля вне цилиндра (r >R) определяется формулой

(τ – линейная плотность).

Разность потенциалов между двумя точками, лежащими на расстоянии r₁ и r₂ (r₁>R; r₂ >R ) от оси цилиндра, равна

(12.32)

• Поле равномерно заряженной бесконечной плоскости

Напряжённость поля этой плоскости определяется формулой

(σ - поверхностная плотность).

Разность потенциалов между точками, лежащими на расстоянии х₁ и х₂ от плоскости, равна

(12.33)

• Поле двух разноименно заряженных бесконечных параллельных плоскостей

Напряженность поля этих плоскостей определяется формулой

Разность потенциалов между плоскостями равна

(12.34)

(d – расстояние между плоскостями).

Примеры решения задач

Пример 12.1. Три точечных заряда Q₁=2нКл, Q₂ =3нКл и Q₃=-4нКл расположены в вершинах равностороннего треугольника со стороной длиной a=10см. Определите потенциальную энергию этой системы.

Дано: Q₁=2нКл=2∙10^-9Кл; Q₂ =3нКл=3∙10^-9Кл; и Q₃=-4нКл=4∙10^-9Кл; a=10см=0,1м.

Найти: U.

Ре шение: Потенциальная энергия системы зарядов равна алгебраической сумме энергий взаимодействия каждой из взаимодействующих пар зарядов, т.е.

U=U₁₂+U₁₃+U₂₃

где соответственно потенциальные энергии одного из зарядов, находящегося в поле другого заряда на расстоянии а от него, равны

;  ; (2)

Подставим формулы (2) в выражение (1), найдём искомую потенциальную энергию системы зарядов

Ответ: U=-0,126мкДж.

Пример 12.2. Определите потенциал в центре кольца с внутренним радиусом R₁=30см и внешним R₂=60см, если на нём равномерно распределён заряд q=5нКл.

Дано: R₁=30см=0,3м; R₂=60см=0,6м; q=5нКл=5∙10^-9Кл

Найти: φ.

Решение: Кольцо разобьём на концентрические бесконечно тонкие кольца внутренним радиусом r и внешним – (r+dr).

Площадь рассматриваемого тонкого кольца (см.рисунок) dS=2πrdr.

По тенциал в центре кольца, создаваемый бесконечно тонким кольцом,

где – поверхностная плотность заряда.

Для определения потенциала в центре кольца следует арифметически сложить dφ от всех бесконечно тонких колец. Тогда

Учитывая, что заряд кольца Q=σS, где S= π(R₂²-R₁²)- площадь кольца, получим искомый потенциал в центре кольца

Ответ: φ=25В

Пример 12.3. Два точечных одноименных заряда (q₁=2нКл и q₂=5нКл) находятся в вакууме на расстоянии r₁= 20см. Определите работу А, которую надо совершить, чтобы сблизить их до расстояния r₂=5см.

Дано: q₁=2нКл=2∙10^-9Кл; q ₂=5нКл=5∙10^-9Кл; r₁= 20см=0,2м; r₂=5см=0,05м.

Найти: А.

Решение: Работа, совершаемая силами электростатического поля при перемещении заряда Q из точки поля, имеющей потенциал φ₁, в точку с потенциалом φ₂.

A₁₂= q(φ₁- φ₂)

При сближении одноимённых зарядов работу совершают внешние силы, поэтому работа этих сил равна по модулю, но противоположна по знаку работе кулоновских сил:

A= -q(φ₁- φ₂)= q(φ₂- φ₁). (1)

Потенциалы точек 1 и 2 электростатического поля

;  (2)

Подставив формулы (2) в выражение (1), найдём искомую работу, которую надо совершить, чтобы сблизить заряды,

Ответ: А=1,35 мкДж.

Пример 12.4. Электростатическое поле создаётся положительно заряженной бесконечной нитью. Протон, двигаясь под действием электростатического поля вдоль линии напряжённости от нити с расстояния r₁=2см до r₂=10см, изменил свою скорость от υ₁=1Мм/с до υ₂=5Мм/с. Определите линейную плотность τ заряда нити..

Дано: q=1,6∙10^-19 Кл; m=1,67∙10^-27кг; r₁=2см=2∙10^-2м; r₂= 10см=0,1м; r₂=5см=0,05м; υ₁=1Мм/с=1∙10⁶м/с; до υ₂=5Мм/с=5∙10⁶м/с.

Найти: τ.

Решение: Работа, совершаемая силами электростатического поля при перемещении протона из точки поля с потенциалом φ₁ в точку с потенциалом φ₂ идёт на увеличение кинетической энергии протона

q(φ₁- φ₂)=ΔТ (1)

В случае нити электростатическое поле обладает осевой симметрией, поэтому

или dφ=-Edr,

тогда разность потенциалов между двумя точками, находящимися на расстоянии r₁ и r₂ от нити,

(учли, что напряжённость поля, создаваемого равномерно заряженной бесконечной нитью,  ).

Подставив выражение (2) в формулу (1) и учитывая, что  , получим

Откуда искомая линейная плотность заряда нити

Ответ: τ = 4,33 мкКл/м.

Пример 12.5. Электростатическое поле создаётся в вакууме шаром радиусом R=8см, равномерно заряженными с объёмной плотностью ρ=10нКл/м³. Определите разность потенциалов между двумя точками этого поля, лежащими от центра шара на расстояниях: 1) r₁=10см и r₂=15см; 2) r₃= 2см и r₄=5см..

Дано: R=8см=8∙10^-2м; ρ=10нКл/м³=10∙10^-9нКл/м³; r₁=10см=10∙10^-2м;

r₂=15см=15∙10^-2м; r₃= 2см=2∙10^-2м; r₄=5см=5∙10^-2м.

Найти: 1) φ₁- φ₂; 2) φ₃- φ₄.

Решение: 1) Разность потенциалов между двумя точками, лежащими на расстоянии r₁ и r₂ от центра шара.

(1)

где  - напряжённость поля, создаваемого равномерно заряженным с объёмной плотностью ρ шаром, в любой точке, лежащей вне шара на расстоянииr от его центра.

Подставив это выражение в формулу (1) и проинтегрировав, получим искомую разность потенциалов

2) Разность потенциалов между двумя точками, лежащими на расстоянии r₃ и r₄ от центра шара,

(2)

где  - напряжённость поля, создаваемого равномерно заряженным с объёмной плотностью ρ шаром, в любой точке, лежащей внутри шара на расстоянииr от его центра.

Подставив это выражение в формулу (2) и проинтегрировав, получим искомую разность потенциалов

Ответ: 1) φ₁- φ₂=0,643 В; 2) φ₃- φ₄=0,395 В

Работа электростатического поля

Рассмотрим ситуацию: заряд q₀ попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q₀ со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.

Потенциал

Система "заряд - электростатическое поле" или "заряд - заряд" обладает потенциальной энергией, подобно тому, как система "гравитационное поле - тело" обладает потенциальной энергией.

Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал - это характеристика электростатического поля.

Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.

Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.

В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело - наоборот.

Потенциальная энергия поля - это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.

Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.

Разность потенциалов

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов

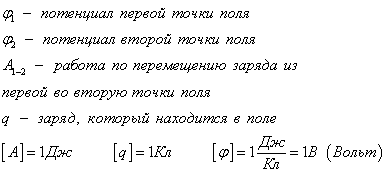
Эту формулу можно представить в ином виде

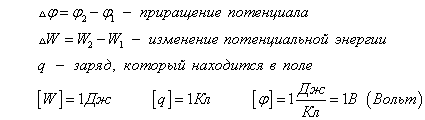
Эквипотенциальная поверхность (линия) - поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Напряжение

Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.

Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.

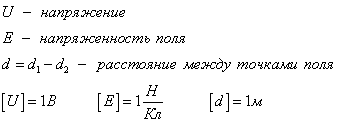
От величины напряжения зависит ток в цепи и энергия заряженной частицы.

Принцип суперпозиции

Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности

Как определить знак потенциала

Зависимость напряженности и потенциала от расстояния

Напряжение в природе

Энергия взаимодействия зарядов*