5.2. Диэлектрики в постоянном поле. Уравнение Клаузиуса[1]–Моссотти[2]

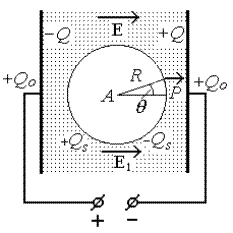
Рассмотрим свойства диэлектриков в статических полях. Связь между макроскопическими и микроскопическими параметрами вещества, то есть между диэлектрической проницаемостью диэлектрика и поляризацией его молекул, устанавливает уравнение Клаузиуса–Моссотти.

Поле, которое действует на отдельную молекулу, может заметно отличаться от среднего макроскопического E. Как показал Лоренц[3], напряженность локального поля можно представить в виде суммы

 . (5.4)

Физический смысл   и   поясним на следующем примере. Пусть молекула находится в точке А заряженного диэлектрического конденсатора (рис.5.1). Опишем вокруг молекулы сферу, радиус Rкоторой значительно больше радиуса молекулы, так что за пределами сферы можно считать диэлектрик однородным. Мысленно извлечем из сферы все вещество за исключением рассматриваемой молекулы. На поверхности сферы будет индуцироваться связанный заряд, поверхностная плотность  которого определяется нормальной к поверхности составляющей вектора поляризации P:

 . (5.5)

Этот индуцированный заряд и создает поле   . Поле   создается в точке А молекулами, расположенными внутри сферы. Можно показать, что в большинстве случаев   (в частности, для газов, неполярных жидкостей и твердых тел).

Вычислим поле Лоренца   . Элемент площади поверхности сферы   создает в точке Аполе, направленное по радиусу:

 .

Рис. 5.1. Схема к расчету поля Лоренца

Проекция вектора этого поля на направление среднего поля есть

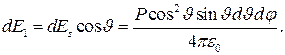
Проинтегрировав по всей поверхности, получим для поля Лоренца выражение

 . (5.6)

Следовательно, напряженность локального поля равняется

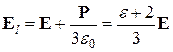 . (5.7)

Здесь мы воспользовались соотношением (5.3). Электрический момент единицы объема диэлектрика можно выразить через локальное поле

 , (5.8)

где   – концентрация молекул, которые принимают участие в поляризации,   – поляризуемость отдельной молекулы. Подстановка (5.7) в (5.8) дает

 . (5.9)

Приравнивая правые части (5.3) и (5.9), получаем уравнение Клаузиуса–Моссотти

 . (5.10)

При наличии молекул разного сорта уравнение (5.10) перепишется в виде

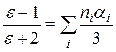 , (5.11)

где суммирование осуществляется по всем типам молекул.

Основные определения

Поляризация – состояние диэлектрика, при котором элементарный объем материала приобретает электрический момент (под действием электрического поля, механических напряжений или спонтанно в сегнетоэлектриках).

Поляризованность – количественная характеристика поляризации, определяющая ее интенсивность – вычисляется как P = dp/dV – отношение электрического момента dp элемента диэлектрика к объему этого элемента. [Кл/м²].

P = ₀(-1)E = ₀χE. – для большинства диэлектриков (кроме сегнетоэлектриков) в слабых электрических полях. χ – диэлектрическая восприимчивость.

Любой диэлектрик с нанесенными на него электродами, включенный в электрическую цепь, можно рассматривать как конденсатор (рисунок  2.1) .

Рис. 2.1. Конденсатор с диэлектриком

 

Q₀ – заряд на обкладках конденсатора. Q_д – заряд, возникающий на краях диэлектрика из-за поляризации в электрическом поле.

Полный заряд конденсатора с диэлектриком: Q = Q₀ + Q_д = * Q₀

 – относительная диэлектрическая проницаемость – отношение суммарного заряда конденсатора с диэлектриком к заряду конденсатора в вакууме без диэлектрика м/у его обкладками :  = Q/Q₀  = (Q_д+Q₀)/Q₀ = 1+ Q_д/Q₀

_а = ₀ – абсолютная диэлектрическая проницаемость. ₀ =  8.854*10^-12 Ф/м – электрическая постоянная.