
- •Энергия. Работа и кинетическая энергия. Теорема кенига
- •Величина (4.4)
- •Потенциальное поле сил. Консервативные и неконсервативные силы
- •Потенциальная энергия во внешнем поле сил. Связь между силой и потенциальной энергией. Градиент скалярной функции
- •Закон сохранения полной механической энергии в поле консервативных сил
- •Закон сохранения импульса
- •Столкновения тел. Неупругое и абсолютно упругое столкновение
- •Момент импульса материальной точки и механической системы. Момент силы. Уравнение моментов. Закон сохранения момента импульса механической системы
- •Движение в поле центральных сил. Законы кеплера
- •Потенциальная энергия материальной точки во внешнем силовом поле. Ее связь с силой действующей на материальную точку. Понятие о градиенте скалярной функции координат.
- •Энергия кинетическая и потенциальная. Полная механическая энергия и закон ее сохранения. Примеры применения законов сохранения энергии.
- •4. Принцип инерции (первый закон Ньютона). Инерциальные системы отсчета. Принцип относительности.
- •5. Преобразования Галилея.
- •Градиент потенциальной энергии. Связь силы и потенциальной энергии. Движение частицы в потенциальном поле.
Потенциальные силы. Потенциальная энергия. Связь силы с потенциальной энергией. Понятие градиента скалярной функции.
Потенциальные силы. Потенциальная энергия. Связь силы с потенциальной энергией. Понятие градиента скалярной функции.
Градиент—
вектор, показывающий направление
наискорейшего возрастания некоторой
величины, значение которой меняется от
одной точки пространства к другой. Смысл
градиента любой скалярной функции f в
том, что его скалярное произведение с
бесконечно малым вектором перемещения
дает полный дифференциал этой функции
при соответствующем изменении координат
в пространстве, на котором определена
f, то есть линейную (в случае общего
положения она же главная) часть изменения
f при смещении на
![]() .Пространство,
в котором действуют консервативные
силы, называется потенциальным полем.
Каждой точке потенциального поля
соответствует некоторое значение силы
.Пространство,
в котором действуют консервативные
силы, называется потенциальным полем.
Каждой точке потенциального поля
соответствует некоторое значение силы
![]() ,
действующей на тело, и некоторое значение
потенциальной энергии U. Значит, между
силой
и
U должна быть связь
,
действующей на тело, и некоторое значение
потенциальной энергии U. Значит, между
силой
и
U должна быть связь
![]() ,
с другой стороны, dA = –dU, следовательно
,
,
с другой стороны, dA = –dU, следовательно
,
![]() отсюда
отсюда
![]()
Вектор силы можно записать через проекции:
![]() F=-gradU
где
F=-gradU
где
![]()
Следовательно, вектор направлен в сторону наибыстрейшего уменьшения U.
Потенциальная
энергия системы во внешнем поле.
Предположим, что механическая система,
состоящая из n частиц, находится во
внешнем потенциальном поле. Определим
работу, которую совершают внешние
консервативные силы на перемещение
механической системы за элементарный
промежуток времени. Как убедились, любая
частица в потенциальном поле наделена
потенциальной энергией. Обозначим
потенциальные энергии частиц механической
системы как
![]() ,
где
,
где
![]() радиус-векторы,
характеризующие положения частиц.
Покажем, что потенциальная энергия
системы во внешнем потенциальном поле
есть сумма потенциальных энергий
составляющих систему частиц:
радиус-векторы,
характеризующие положения частиц.
Покажем, что потенциальная энергия
системы во внешнем потенциальном поле
есть сумма потенциальных энергий
составляющих систему частиц:
![]() Пусть
частицы системы за элементарный
промежуток времени dt
совершили перемещения
Пусть
частицы системы за элементарный
промежуток времени dt
совершили перемещения
![]() .
Согласно результату, полученному выше,
работа сил поля на перемещение любой
частицы равна убыли потенциальной
энергии этой частицы:
.
Согласно результату, полученному выше,
работа сил поля на перемещение любой
частицы равна убыли потенциальной
энергии этой частицы:
![]() Суммируя
эти элементарные работы, получим полную
работу внешних консервативных сил на
перемещение системы за время dt:
Суммируя
эти элементарные работы, получим полную
работу внешних консервативных сил на
перемещение системы за время dt:
![]() .
Это доказывает утверждение (6.34): работа
внешних консервативных сил равна убыли
потенциальной энергии системы в силовом
поле:
.
Это доказывает утверждение (6.34): работа
внешних консервативных сил равна убыли
потенциальной энергии системы в силовом
поле:
![]()
Градиент скалярной функции - ϶ᴛᴏ вектор, указывающий направление наиболее быстрого возрастания скалярной функции и по абсолютному значению равный наибольшей скорости возрастания этой функции.
![]()
Градиент направлен по нормали к поверхности равного уровня скалярной функции в данной точке. Градиент скалярного потенциала φ постоянного во времени поля равен:
![]()
где
![]() –
нормаль к эквипотенциальной поверхности
в данной точке поля.
–
нормаль к эквипотенциальной поверхности
в данной точке поля.
Градиент
скалярного потенциала φ в каждой точке
совпадает с касательной к силовой линии
напряженности электрического поля
![]() в
данной точке и имеет направление,
противоположное вектору
в
данной точке и имеет направление,
противоположное вектору
Потенциальная
энергия
![]() —
скалярная физическая величина,
представляющая собой часть полной
механической энергии системы, находящейся
в полеконсервативных сил. Зависит от
положения материальных точек, составляющих
систему, и характеризует работу,
совершаемую полем при их перемещении.
Термин ʼʼпотенциальная энергияʼʼ был
введен в XIX веке шотландским инженером
и физиком Уильямом Ренкином.
—
скалярная физическая величина,
представляющая собой часть полной
механической энергии системы, находящейся
в полеконсервативных сил. Зависит от
положения материальных точек, составляющих
систему, и характеризует работу,
совершаемую полем при их перемещении.
Термин ʼʼпотенциальная энергияʼʼ был
введен в XIX веке шотландским инженером
и физиком Уильямом Ренкином.
Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.
Потенциальная
энергия тела
![]() в
поле тяготения Земли вблизи поверхности
приближённо выражается формулой:
в
поле тяготения Земли вблизи поверхности
приближённо выражается формулой:
![]()
где
![]() —
масса тела,
—
масса тела,
![]() —
ускорение свободного падения,
—
ускорение свободного падения,
![]() —
высота положения центра масс тела над
произвольно выбранным нулевым уровнем.
—
высота положения центра масс тела над
произвольно выбранным нулевым уровнем.
ЭНЕРГИЯ. РАБОТА И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ. ТЕОРЕМА КЕНИГА
ЗАКОНЫ СОХРАНЕНИЯ
СОХРАНЯЮЩИЕСЯ ВЕЛИЧИНЫ
Для замкнутых систем существуют такие функции координат и скоростей образующих систему частиц, которые сохраняют при движении постоянные значения. Эти функции называются интегралами движения.
Для
системы из
![]() частиц,
между которыми нет жестких связей, можно
образовать
частиц,
между которыми нет жестких связей, можно
образовать
![]() интегралов
движения. Однако интерес представляют
только те из них, которые обладают
свойством аддитивности. Это свойство
заключается в том, что значение интегралов
движения для системы, состоящей из
частей, взаимодействием которых можно
пренебречь, равно сумме значений для
каждой из частей в отдельности. Аддитивными
интегралами движения являются энергия,
импульс и момент импульса.
интегралов
движения. Однако интерес представляют
только те из них, которые обладают
свойством аддитивности. Это свойство
заключается в том, что значение интегралов
движения для системы, состоящей из
частей, взаимодействием которых можно
пренебречь, равно сумме значений для
каждой из частей в отдельности. Аддитивными
интегралами движения являются энергия,
импульс и момент импульса.
Энергия. Работа и кинетическая энергия. Теорема кенига
Энергия является количественной мерой различных форм движения материи и соответствующих им взаимодействий. Движение – неотъемлемое свойство материи. Поэтому любое тело, любая система тел и полей обладают энергией. Энергия характеризует возможные изменения движения системы. Эти изменения происходят вследствие взаимодействия между частями системы, а также между системой и внешней средой. Для различных форм движения и соответствующих им взаимодействий в физике вводят различные виды энергии – механическую, внутреннюю, электрическую и т.д. В механике различают два вида механической энергии: кинетическую и потенциальную.
Кинетической энергией механической системы называется энергия механического движения этой системы.
Изменение механического движения системы происходит только под действием приложенной к ней силы. Поэтому для отыскания вида функции кинетической энергии воспользуемся вторым законом Ньютона.
Рассмотрим
простейшую систему, состоящую из одной
частицы (материальной точки). Уравнение
движения частицы
![]() умножим
на перемещение
умножим
на перемещение
![]() получаем
получаем
![]() .
(4.1)
.
(4.1)
Здесь
![]() -
приращение скорости частицы
-
приращение скорости частицы
![]() за
время
за
время
![]() .
Левую часть выражения (4.1) приведем к
виду:
.
Левую часть выражения (4.1) приведем к
виду:
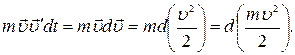 (4.2)
(4.2)
Тогда
имеем:
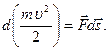
Если
система замкнута, то
![]() ,
и
,
и
![]() ,
а сама величина
,
а сама величина
![]() (4.3)
(4.3)
остается постоянной. Эта величина и называется кинетической энергией. В случае изолированной частицы кинетическая энергия сохраняется и является интегралом движения.
Умножив
на массу частицы
![]() числитель
и знаменатель выражения (4.3) и
воспользовавшись определением импульса,
получаем:
числитель
и знаменатель выражения (4.3) и
воспользовавшись определением импульса,
получаем:
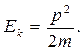
Кинетическая энергия механической системы, состоящей из частиц, равна сумме кинетических энергий отдельных частиц:
![]() .
.
Если
на частицу действует сила
![]() ,
кинетическая энергия не остается
постоянной. Согласно (4.2), приращение
кинетической энергии частицы за время
в
этом случае равно скалярному произведению
,
кинетическая энергия не остается
постоянной. Согласно (4.2), приращение
кинетической энергии частицы за время
в
этом случае равно скалярному произведению
![]() -
перемещение частицы за время
).
Величина
-
перемещение частицы за время
).
Величина
![]() называется
работой, совершаемой силой
на
пути
называется
работой, совершаемой силой
на
пути
![]() ,
где
-
модуль перемещения
,
где
-
модуль перемещения
![]() .
.
Проинтегрировав выражение (4.2) вдоль траектории от точки 1 до точки 2, получаем:
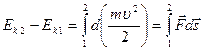 .
.
Величина (4.4)
есть
работа силы
на
пути
![]() .
Таким образом, работа результирующей
всех сил, действующих на частицу, идет
на приращение кинетической энергии
этой частицы:
.
Таким образом, работа результирующей
всех сил, действующих на частицу, идет
на приращение кинетической энергии
этой частицы:
![]() .
(4.5)
.
(4.5)
|
|
|
|
Формула
(4.3) для кинетической энергии частицы
справедлива как в инерциальной, так и
в неинерциальной системе отсчета. При
переходе из одной системы отсчета в
другую, движущуюся относительно первой
с некоторой скоростью
![]() ,
скорость частицы меняется, следовательно,
меняется и кинетическая энергия.
,
скорость частицы меняется, следовательно,
меняется и кинетическая энергия.
Рассмотрим
две системы отсчета: инерциальную
![]() и
систему отсчета
и
систему отсчета
![]() ,
движущуюся относительно
поступательно
со скоростью
.
Скорость
может
быть как постоянной (тогда система
инерциальная),
так и зависящей от времени ( в этом случае
система
неинерциальная).
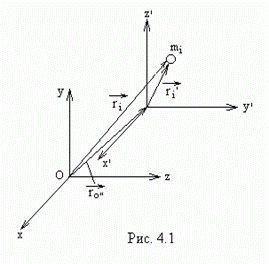
Из рисунка 4.1 видно, что радиус-векторы
,
движущуюся относительно
поступательно
со скоростью
.
Скорость
может
быть как постоянной (тогда система
инерциальная),
так и зависящей от времени ( в этом случае
система
неинерциальная).
Из рисунка 4.1 видно, что радиус-векторы
![]() -той
материальной точки в системах отсчета
и
связаны
соотношением:
-той
материальной точки в системах отсчета
и
связаны
соотношением:
![]() ,
,
где
![]() -
радиус-вектор в системе
точки
-
радиус-вектор в системе
точки
![]() (начала
отсчета координат в системе
).
Продифференцировав это выражение по
времени, получаем для скоростей:
(начала
отсчета координат в системе
).
Продифференцировав это выражение по
времени, получаем для скоростей:
![]() .
.
Возведем
это равенство в квадрат:
![]() .
.
Подставим
значение
![]() в
формулу кинетической энергии механической
системы, получаем кинетическую энергию
относительно системы
:
в
формулу кинетической энергии механической
системы, получаем кинетическую энергию
относительно системы
:
![]() ,
,
или
![]() .
Здесь
-
масса всей системы,
.
Здесь
-
масса всей системы,
![]() -
импульс механической системы в
,
-
импульс механической системы в
,
![]() -
кинетическая энергия системы в
.
-
кинетическая энергия системы в
.
Очевидно,
![]() ,
где
,
где
![]() -
скорость центра масс системы в
.
Поэтому, если в качестве
взять
систему центра масс механической
системы, то
-
скорость центра масс системы в
.
Поэтому, если в качестве
взять
систему центра масс механической
системы, то
![]() и
и
![]() .
.
Это теорема Кенига: кинетическая энергия механической системы равна сумме кинетической энергии той же системы в ее движении относительно центра масс и кинетической энергии, которую имела бы рассматриваемая система, двигаясь поступательно со скоростью центра масс.
 Выражение
(4.4) можно представить в виде:
Выражение
(4.4) можно представить в виде:
![]() где
где
![]() -
угол между направлениями силы и
перемещения. Если этот угол острый (
-
угол между направлениями силы и
перемещения. Если этот угол острый (
![]() ),
работа положительна, если
-
тупой (
),
работа положительна, если
-
тупой (
![]() ),
работа отрицательна. При
),
работа отрицательна. При
![]() работа
равна нулю.
работа
равна нулю.
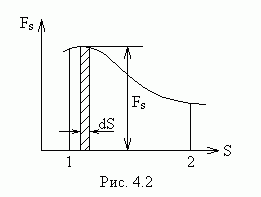
На
рис.4.2 представлен график проекции силы
на направление перемещения
![]() как
функции положения частицы на траектории.
Из рисунка видно, что элементарная
работа
как
функции положения частицы на траектории.
Из рисунка видно, что элементарная
работа
![]() численно
равна площади заштрихованной полоски,
а работа
численно
равна площади заштрихованной полоски,
а работа
![]() на
пути 1-2 численно равна площади фигуры,
ограниченной кривой
,
вертикальными прямыми 1 и 2 и осью S.
на
пути 1-2 численно равна площади фигуры,
ограниченной кривой
,
вертикальными прямыми 1 и 2 и осью S.
Пусть
на тело действует одновременно несколько
сил
![]() .
Из дистрибутивности скалярного
произведения векторов вытекает, что
работа
.
Из дистрибутивности скалярного
произведения векторов вытекает, что
работа
![]() ,
совершаемая результирующей силой на
пути
,
может быть представлена в виде:
,
совершаемая результирующей силой на
пути
,
может быть представлена в виде:
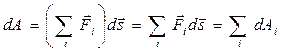
- работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой силой в отдельности.
Очевидно,
элементарное перемещение
![]() ,
поэтому выражение для элементарной
работы (4.4) принимает вид:
,
поэтому выражение для элементарной
работы (4.4) принимает вид:
![]()
Тогда
работа, совершаемая за промежуток
времени от
![]() до
до
![]() ,
будет равна
,
будет равна
![]()
Работа,
совершаемая в единицу времени, называется
мощностью:
![]() .
.
Проинтегрировав
выражение (4.2) вдоль траектории от точки
1 до точки 2, получаем:
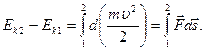 Величина
Величина
![]()
есть работа силы на пути . Таким образом, работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии этой частицы:
![]()
