1. Импульс может сохра­няться и для незамкнутой сис­темы при условии, что ре­зультирующая всех внешних сил равна нулю.

2. У незамкнутой системы может сохраняться не сам импульс , а его проекция P_х на некоторое направле­ние х. Причина этого заключается в том, что когда проекция результирующей внешней силы на направление х равна нулю, т. е. вектор перпендикулярен ему. Действительно, спрое­ктировав уравнение (2.16),получим

,

откуда следует, что если , то P_x=const. Напри­мер, при движении системы в однородном поле сил тя­жести сохраняется проекция ее импульса на любое гори­зонтальное направление независимо от процессов, происходящих в системе. При горизонтальном перемещении человека в первоначально покоящейся лодке, импульс системы человек-лодка лодка будет равен нулю. Центр масс системы человек-лодка будет неподвижен, так как сумма внешних сил в горизонтальном направлении равна нулю (если пренебречь силами сопротивления) и согласно (2.14) скорость центра масс также равна нулю.

Пример 2.1. Найти закон движения материальной точки, движущейся по прямой под действием упругой силы F = –kx. Движение начинается из начала координат x=0 в момент времени t = 0 с начальной скоростью υ₀.

Уравнение (2.3) в одномерном случае ( ) примет вид:

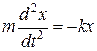. (2.17)

Это дифференциальное уравнение с постоянными коэффициентами. Из математики известно, что решение этого дифференциального уравнения имеет вид:

. (2.18)

Константы A и φ найдем из начальных условий:

.

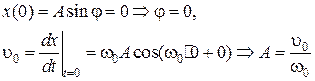Значение ω₀ определим, подставив решение (2.18) в уравнение (2.17):

.

Искомый закон имеет вид:

.

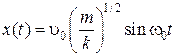Движение, которое задано синусоидальной функцией (2.18), называется гармоническим колебанием. Величина w₀ есть циклическая частота собственных колебаний материальной точки, А – амплитуда колебаний, φ - начальная фаза.

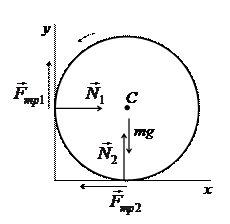
Пример 2.2. Применение закона движения центра масс для расчета сил трения скольжения.

Однородный цилиндр массой m равномерно вращается между двумя взаимно перпендикулярными плоскостями (рис. 2.3). Коэффициент трения скольжения цилиндра о плоскости равен m. Найти силы трения скольжения.

На цилиндр действуют силы трения и , силы реакции со стороны плоскостей, и и сила тяжести mg (рис. 2.3), которые являются внешними, т. е. обусловлены действием внешних тел. Центр масс цилиндра (точка, которая лежит на оси цилиндра С) неподвижен. Поэтому левая часть уравнения (2.14) равна нулю. Перепишем это уравнение в проекциях на оси x и y:

(2.19)

Силы трения скольжения равны F_тр1 = mN₁ и F_тр2 = mN₂ . Подставив эти выражения в (2.19), получим:

Рис. 2.3

Умножим второе уравнение в (2.19) на μ и сложим с первым:

.

Отсюда найдем силу N₁ :

.

Сила трения F_тр1 равна:

.

Из первого уравнения в (2.19) выразим силу N₂= N₁/m и найдем силу трения F_тр2:

.

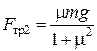https://studopedia.ru/3_33846_impuls-mehanicheskoy-sistemi-zakon-sohraneniya-impulsa-zamknutoy-sistemi.html

ЗАКОНЫ СОХРАНЕНИЯ

Законы сохранения – это в некотором смысле альтернатива динамическому подходу. Конечно, в принципе, динамика Ньютона позволяет решить любую задачу. Но при этом часто возникают препятствия, которые можно разбить на два основных класса: • Уравнения динамики могут плохо поддаваться решению, особенно для сложных систем. Часто динамическое описание оказывается излишне детализированным. Нас, может быть, ряд тонкостей вообще не интересует, однако мы вынуждены всякий раз составлять большие системы уравнений и пытаться их решать. • Динамика требует знания всех важных сил. Между тем ясно, что все существующие в природе силы никогда не будут точно известны. В особенности это касается внутренних взаимодействий в любом реальном теле. Законы сохранения в ряде случаев позволяют избежать указанных трудностей, и практически во всех случаях – сделать хотя бы качественные, но тем не менее полезные выводы о движении.