1. В чем заключается метод баллистического маятника для определения скорости быстро движущегося тела?

При расчёте скорости полёта, исходя из опытных данных, используется закон сохранения момента импульса при неупругом ударе и закон сохранения полной механической энергии после его завершения.

2. Скорость.Физический смысл. Средняя и мгновенная скорость поступательной величины.Единицы измерения

Скорость — физическая величина, характеризующая движение тела в пространстве. Физический смысл - Изменение координаты в единицу времени. Средняя скорость движения характеризует быстроту изменения пути во времени. Мгновенная скорость (обычно используется термин скорость) характеризует быстроту изменения радиуса-вектора материальной точки во времени. Единицы измерения: Километр в час, Метр в секунду

3. Механическая система

Механическая система — это совокупность взаимодействующих другу с другом и с внешними телами материальных точек, движение которых подчиняется согласно законам классической механики.

4. Импульс тела.Единица измерения

Импульс тела - это физическая векторная величина, равная произведению массы тела на его скорость. Измеряется кг*м/с

5. Полный импульс механической системы

закон сохранения импульса в замкнутой системе, который формулируют так: полный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел этой системы между собой.

6.замкнута механическая система

Замкнутой механической системой точек мы называем такую систему, в которой движение частиц обусловлено только силами взаимодействия, или внутренними силами

7.Закон сохранения импульса замкнутой механической системы в общем виде и его применение для данной работы

p=p₁+p₂=const.

Формула выражает закон сохранения импульса в замкнутой системе, который формулируют так: полный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел этой системы между собой. Иными словами, внутренние силы не могут изменить полного импульса системы ни по модулю, ни по направлению.

8.понятие энергии.кинетическая энергия тела.единицы измерения

Энергия - общая количественная мера движения и взаимодействия всех видов материи. кинетической энергией называется  величина, равная половине произведения массы тела на квадрат его скорости.  [Ek]=Дж 

9. потенциальная энергия тела,поднятого над поверхностью земли.потенциальная энергия сжатой пружины

Потенциальная энергия - энергия взаимодействия тел или частей тела

В еличина mgh - это потенциальная энергия тела, поднятого на высоту h над нулевым уровнем.

это потенциальная энергия сжатой пружины

10.закон сохранения механической энергии.условия его выполнения.применение этого закона на данной работы

Если в замкнутой системе не действуют силы, трения и силы сопротивления, то сумма кинетической и потенциальной энергии всех тел системы остается величиной постоянной.

11.упругий и неупругий удары

- абсолютно упругий, при котором полная механическая энергия сохраняется, то есть внутренняя энергия частиц не меняется. Во взаимодействующих телах не остается деформаций.

 Абсолютно неупругий, при котором частицы «слипаются», двигаясь дальше как единое целое или покоясь. Кинетическая энергия частично или полностью превращается во внутреннюю.

12 вывод расчетной формулы

При соударении пули с маятником справедлив закон сохранения импульса

, (6.1)

где m – масса пули, M – масса маятника, v – скорость пули, V – скорость маятника непосредственно после удара.

Чтобы определить величину V, нужно измерить высоту h, на которую поднимается маятник после удара. Из закона сохранения энергии получается

. (6.2)

Соотношения (6.1) и (6.2) дают

. (6.3)

Высоту подъема центра масс маятника можно определить из рис. 13:

,

где R-расстояние от шкалы с миллиметровыми делениями до уровня подвеса маятника.

Учитывая, что hR, получаем: 2Rh = s². Определяя отсюда h и подставляя в (6.3), получаем рабочую формулу метода

. (6.4)

https://studfiles.net/preview/4405261/

Сила и масса. Второй закон динамики

Динамики

Инерциальные системы отсчета. Первый закон

Основные законы динамики

ОСНОВЫ ДИНАМИКИ

ЛЕКЦИЯ 2

Динамика представляет собой раздел механики, в котором изучается движение тел под действием приложенных сил.

Основной задачей динамики является определение кинематического уравнения движения материальной точки, если известны все силы, приложенные к ней со стороны окружающих тел. Динамика рассматривает также и обратную задачу - определение законов взаимодействия точки с окружающими телами, если известен кинематический закон движения. В основе динамики лежат три закона И. Ньютона, Движение тел описывается законами И. Ньютона, если скорость движения тел много меньше скорости света в вакууме, а масса их намного больше массы атомов или молекул.

При отсутствии воздействия со стороны других тел материальная точка является свободной и движется отно­сительно такой системы отсчета прямолинейно и равно­мерно. Такую систему от­счета называют инерциальной.

Закон инерции: материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пока воздействие со стороны других тел не выведет ее из этого состо­яния. Си­стемы отсчета, движущиеся с ускорением относительно инерциальных систем, называют неинерциальными. Воздействие тела (или тел), вызывающее уско­рение данного тела называют силой. Поэтому, причиной ускоре­ния тела является действующая на него сила. Все силы, обычно подразделяют на силы, возникающие при непосредствен­ном контакте тел (силы давления, трения), и силы, воз­никающие через посредство полей, которые создаются взаимодейству­ющими телами (например, гравитационные, электрические или магнитные силы). Опыты показывают, что две силы, приложенные одновременно в одной и той же точке тела, можно уравновесить одной силой. Эта сила численно равна и противоположна по направлению геометрической сумме указанных двух сил, определяемой по известному правилу параллелограмма. Следовательно, силы складываются по правилу сложения векторов, т. е, сила - величина векторная. Сила, приложен­ная к телу, полностью определена, если указаны ее численное значение, направление действия и точка приложения. Если на две точки с разными массами m₁ и m₂ действует одинаковая сила, то отношение ускорений, сообщаемых этим точкам, равно . Из последнего равенства следует, что произведение массы материальной точки на ее ускорение для обеих точек будет одинаковым. Это произведение равно силе, действующей на эти точки. Поэтому, сила , сообщающая точке ускорение , справедливо соотношение:

. (2.1)

Уравнение (2.2) называют уравнением движения мате­риальной точки.Подставив вместо ускорения его выражение (1-2) и выразив его через вторую производную от радиус-вектора по времени, получим дифференциальное уравнение, которое называется дифференциальным уравнением движения материальной точки:

. (2.2)

Если на материальную точку одновременно действуют силы , то, как показывает опыт, их можно заменить одной эквивалентной им силой , равной их геометрической сумме и приложенной в той же точке:

, (2.3)

где - сила, с которой действовало бы на данную ма­териальную точку i-e тело в отсутствие других тел. Формула (2.3) является выражением принципа суперпозиции для сил . Силу называют резуль­тирующей, или равнодействующей, силой.

Первое уравнение (2.2) можно представить в виде:

. (2.4)

Вектор называется импульсом материальной точки.Импульс точки является динамической характеристикой и определяется ее массой и скоростью движения. Последнее равенство, записанное в виде:

, (2.5)

является выражением второго закона динамики Ньютона. Этот закон можно сформулировать следующим образом: скорость изменения импульса точки равна равнодействующей силе, которая действует на данную точку.

Перепишем второй закон Ньютона (2.5) в следующем виде:

Произведение называют элементарным импульсом силы за малый промежуток времени ее действия dt. Изменение импульса материальной точки за конечный промежуток времени от t до t + Δ t получим интегрированием последнего выражения в пределах от t до t + Δ t:

, (2.6)

где - импульс результирующей силы за рассматриваемый промежуток времени Δ t. В общем случае, если сила меняется во времени, то (2.6) можно переписать виде:

., (2.7)

где - среднее значение переменной силы в интервале времени Δt

https://studopedia.ru/3_33843_sila-i-massa-vtoroy-zakon-dinamiki.html

Системы материальных точек. Закон движения центра масс

Любое абсолютно твердое тело можно представить как совокупность жестко связанных элементарных объемов, или как систему материальных точек. Для описания динамики системы точек широко применяется понятие центра масс системы. Центром масс системы материальных точек называют точку С, радиус - вектор которой определяется формулой:

, (2.9)

где m_i и - масса и радиус – вектор i-ой точки системы. Соответственно соотношения для координат центра масс системы равны

, и .

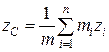Скорость центра масс системы получим, дифференцируя выражение (2.10) по времени:

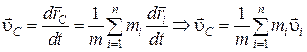. (2.10)

Ускорение центра масс:

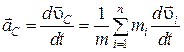. (2.11)

Рассмотрим систему, состоящую из n материальных точек. Силы, действующие на точки системы, можно подразделить на внутренние и внешние.

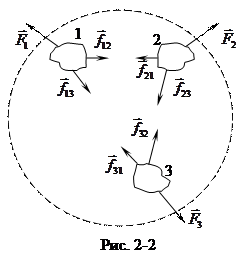
Внутренними называются силы, с которыми точки системы действуют друг на друга, а внешние - силы, обусловленные действием тел, не принадлежащих данной системе. Если внешние силы отсутствуют, система называется замкнутой. Обозначим внутреннюю силу, действующую i-юна точку системы со стороны k-й точки (рис. 2.2), а - равнодействующую внешних сил, действующих на i-ю точку. Запишем второй закон Ньютона через скорость в виде (2.2) для трех частиц:

Сложим правые и левые части этих трех уравнений, учитывая, что сумма всех внутренних сил согласно 3-му закону динамики равна нулю и используя 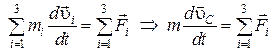(2.12):

, (2.12)

где m = m₁ + m₂ + m₃.

Для системы из n точекуравнение (2.13) примет вид:

(2.13)

где

Уравнение (2.13) выражает теорему о движении центра масс системы: центр масс любой системы материальных точек движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы. При этом ускорение центра масс не зави­сит от точек приложения внешних сил.

https://studopedia.ru/3_33845_sistemi-materialnih-tochek-zakon-dvizheniya-tsentra-mass.html

Импульс механической системы. Закон сохранения импульса замкнутой системы

Рассмотрим систему материальных точек. Импульс системы равен геометрической сумме импульсов всех n материальных точек системы:

.

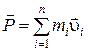Преобразуя последнее равенство и используя формулу (2.11), получим:

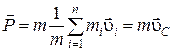. (2.14)

Из (2.14) следует, что импульс системы точек равен произведению массы всей системы на скорость ее центра масс.

Преобразовав уравнение (2.13) с учетом выражения (2.14), получим,

. (2.15)

Уравнение (2.16) выражает теорему об изменении импульса системы: скорость изменения импульса механической системы равна сумме всех внешних сил, приложенных к системе.Согласно уравнению (2.15), импульс системы может изменяться под действием только внешних сил. Внутрен­ние силы не могут изменить импульс системы.

Замкнутой системой называют систему точек, на которую не действуют внешние силы. Для замкнутой системы правая часть уравнения (2-15) равна нулю:

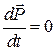или .

Полученное равенство выражает собой закон сохранения импульса: импульс замкнутой системы не изменяется со временем. При этом импульсы отдельных точек или частей замкну­той системы могут меняться со временем:

,.

однако эти изменения всег­да происходят так, что приращение импульса одной час­ти системы равно убыли импульса оставшейся части системы.