Атом водорода. Радиус и энергия электронных орбит в атоме водорода. Серии атома водорода. Постоянная Ритберга.

Теория Бора водородоподобных атомов.

Нильс Бор создал теорию строения атома, способную объяснить опыты Резерфорда и спектр излучения паров водорода.

Спектр характеризует распределение интенсивности излучения по шкале частот (или по шкале длин волн).

Постулаты Бора.

1-й постулат:

электрон в атоме может двигаться только по определенным стационарным орбитам, находясь на которых, он не излучает и не поглощает энергию. Момент импульса электрона на этих орбитах кратен постоянной Планка:

, (1)

m_e – масса электрона, - скорость электрона на орбите с номеромn, r_n – радиус орбиты с номером n, n =1,2,3,….

Дж·с – постоянная Планка.

2-й постулат:

при переходе электрона с одной стационарной орбиты на другую излучается или поглощается фотон, энергия которого

. (2)

E _n1 и E _n2 - энергия электрона в состоянии 1 и 2 (т.е. на орбитах 1 и 2), - частота электромагнитных волн, - постоянная Планка.

Радиус орбиты электрона в атоме водорода.

1-й постулат Бора, .

Выразим скорость электрона:

. (3)

Рассмотрим круговые электронные орбиты. На электрон с зарядом -e со стороны ядра с зарядом +e действует сила Кулона F, сообщая электрону нормальное ускорение,

.

По 2-му закону Ньютона,

. (4)

Сократим и подставим скорость из (3):

.

Отсюда

.

Радиус первой орбиты электрона (n = 1), называется радиусом Бора ,

= 0.53·10^-10 м.

Радиус орбиты электрона в атоме водорода

, n =1,2,3,…. – номер орбиты.

Энергия электрона в атоме водорода.

Энергия электрона представляет собой сумму кинетической энергии и потенциальной .

и .

Потенциальная энергия – это энергия электрона с зарядом в электрическом поле ядра. Из уравнения (4) видно, что

.

Тогда на n –ой орбите энергия электрона равна

= = .

Т.е. кинетическая энергия электрона равна полной энергии, взятой со знаком «-».

Также полную энергию можно записать через потенциальную:

= , или

.

Подставим . Тогда

= .

Энергия на первой орбите (на первом энергетическом уровне) равна

= = -13,6 эВ.

Величину = 13,6 эВ = 2,18∙10^-18 Дж называют энергией ионизации (эта энергия необходима, чтобы перевести электрон, находящийся на первом уровне, в свободное состояние, т.е. чтобы ионизовать атом). Окончательно, энергия электрона на n –ом энергетическом уровне (на n –ой орбите) записывается как

= .

Спектр излучения водорода.

Энергия излучаемого или поглощаемого кванта:

.

Частота , длина волны, - скорость света в вакууме.

= + = ,

= .

= - формула Бальмера,

определяет длины волн в спектре атома водорода.

= 1,1∙10⁷ м^-1 - постоянная Ридберга.

и - номера энергетических состояний (номера орбит) электрона.

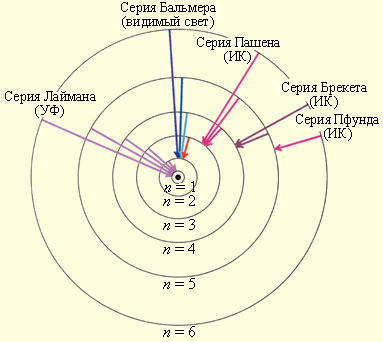
Переходы электрона с возбужденных энергетических состояний на основной энергетический уровень ( = 1) сопровождаются излучением вУФ области спектра (серия линий Лаймана),

переходы на уровень с = 2 приводят к линиямв видимой области (серия Бальмера),

переходы на уровень с = 3, 4, 5, … приводят излучению вИК области.

Теория Бора не смогла объяснить строение сложных атомов. Для объяснения поведения микрочастиц была развита квантовая механика.

Она основана на том, что любая микрочастица, наряду с корпускулярными, обладает также волновыми свойствами (гипотеза де Бройля).

Для фотона, импульс

.

По аналогии с фотоном, любую микрочастицу можно рассматривать как волну с длиной волны

,

- длина волны де Бройля.

Гипотеза де Бройля подтверждена экспериментально наблюдением дифракции электронов, а затем и протонов.

Принцип неопределенностей.

Первая попытка создания на основе накопленных экспериментальных данных модели атома принадлежит Дж. Дж. Томсону (1903). Согласно этой модели, атом представляет собой непрерывно заряженный положительным зарядом шар радиусом порядка 10^{-10 м, внутри которого около своих положений равновесия колеблются электроны; суммарный отрицательный заряд электронов равен положительному заряду шара, поэтому атом в целом нейтрален. Через несколько лет было доказано, что представление о непрерывно распределенном внутри атома положительном заряде ошибочно.}

Рис. 3.6

В развитии представлений о строении атома велико значение опытов английского физика Э. Резерфорда (1871 —1937) по рассеянию a-частиц в веществе. Альфа-частицы возникают при радиоактивных превращениях; они являются положительно заряженными частицами с зарядом 2е и массой, примерно в 7300 раз большей массы электрона. Резерфорд, исследуя прохождение a-частиц в веществе, показал, что основная их часть испытывает незначительные отклонения, но некоторые a-частицы (примерно одна из 20 000) резко отклоняются от первоначального направления (углы отклонения достигали даже 180°). Резерфордом был сделан вывод, что значительное отклонение a-частиц обусловлено их взаимодействием с положительным зарядом большой массы, которая сосредоточен в объеме, очень малом по сравнению с объемом атома.

На основании своих исследований Резерфорд в 1911 г. предложил ядерную (планетарную) модель атома. Согласно этой модели, вокруг положительного ядра, имеющего заряд Ze (Z — порядковый номер элемента в системе Менделеева, е — элементарный заряд), размер 10^-15 - 10^-14 м и массу, практически равную массе атома, в области с линейными размерами порядка 10^{-10 м по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Так как атомы нейтральны, то заряд ядра равен суммарному заряду электронов, т. е. вокруг ядра должно вращаться Z электронов.}

Однако электрон, движущийся ускоренно по окружности под действием кулоновской силы, согласно электродинамике, должен излучать электромагнитные волны и вследствие этого непрерывно терять энергию. В результате электрон будет приближаться к ядру и в конце концов упадет на него. Атом Резерфорда, с точки зрения классической физики, оказывается неустойчивой системой, что противоречит действительности.

Первая попытка построить качественно новую — квантовую — теорию атома была предпринята в 1913 г. датским физиком Нильсом Бором. Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовый характер излучения и поглощения света.

Чтобы объяснить устойчивость атома датский физик Нильс Бор постулировал основные положения (постулаты Бора), которые явили собой первую квантовую модель атома.

Постулаты Бора:

1. Электроны в атоме движутся по некоторым стационарным орбитам. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.

2. В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию квантования момента импульса электрона

Рис.3.7

(3.5.1)

n = 1,2,3…– главное квантовое число (номер орбиты-уровня), m_e - масса элетрона, v — его скорость на n-ой орбите радиуса r_n, , h = 6,62·10^-34 Дж·с – постоянная Планка;

3. При переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией:

(3.5.2)

равной разности энергий соответствующих стационарных состояний (Е_n и Е_m — соответственно энергии стационарных состояний атома до и после излучения (поглощения). При Е_n > Е_m происходит излучение фотона (переход атома из состояния с большей энергией в состояние меньшей энергией, т. е. переход электрона с более удаленной от ядра орбиты на более близлежащую), при Е_n < Е_m — его поглощение (переход атома в состояние большей энергией, т. е. переход электрона на более удаленную от ядра орбиту). Набор возможных дискретных частот

(3.5.3)

квантовых переходов определяет линейчатый спектр атома. Излучение атома представляет не непрерывный спектр, а спектр, состоящий из отдельных линий, соответствующих определенным частотам.

Используя постулаты Бора, закон Кулона и вращение электрона по круговой орбите, можно рассчитать величину радиуса орбиты r_n и скорость электрона на ней v_n:

n=1,2,3… (3.5.4)

, (3.5.5)

где m – масса электрона;

ε₀ – электрическая постоянная:

z – порядковый номер элемента;

е – заряд ядра.

Полная энергия Е орбитального электрона равна сумме его кинетической и потенциальной энергий:

Е_n = Е_кинn + Е_потn

(3.5.6)

Для атома водорода (Z=1) радиус первой орбиты электрона при n=1, называемый первым боровским радиусом, равен r₁ = 0,528 10^{-10 м.} Энергия электрона в водородоподобном атоме может принимать следующие дискретные значения:

n=1,2,3… (3.5.7)

Полная энергия электрона в атоме – величина отрицательная (Е_n<0), т.е. электроны в атоме движутся как в потенциальной яме.

Электроны, находясь на стационарных орбитах, обладают потенциальной энергией, максимальная величина которой будет ¥, то есть будет соответствовать ионизованному атому. Там она будет равна нулю, следовательно, потенциальная энергия электрона в атоме отрицательна.

Целое число n в выражении, определяющее энергетические уровни атома, называется главным квантовым числом. Энергетический уровень с n = 1 является основным (нормальным); состояния с n>1 являются возбужденными.

Из представленных выше формул можно получить выражение для частоты излучения при переходе электрона с одного энергетического уровня на другой

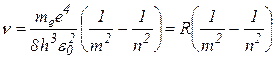
(3.5.8)

 

R – постоянная Ридберга, для атома водорода R=3.29 10¹⁵ c^-1.

 

 

Рис. 3.8.

 

При переходе электрона с произвольного возбужденного уровня на уровень с фиксированным значением m получим набор частот (группу линий в спектре атома) который называется серией. Так в атоме водорода переход на основной уровень (m=1) c произвольного возбужденного уровня (n=2,3,4…) определяет серию Лаймана; переход на уровень с m=2 c уровня n=3,4,5… определяет серию Бальмера; переход на уровень с m=3 c уровня n=4,5,6… определяет серию Пашена и т.д.

Переход с более удаленной орбиты на более близкую связан с испусканием одного фотона – такова причина возникновения линейчатого спектра испускания, а переход электрона на более дальнюю орбиту при поглощении фотона соответствует возникновению линейчатогоспектра поглощения.

Атомные спектры обладают ярко выраженной индивидуальностью, причем их вид определяется не только атомом данного элемента, но и его строением, внешними факторами: температурой, давлением, электрическими и магнитными полями и др.

Получение и анализ спектров играют огромную роль в теоретической и прикладной физике и технике. Изучение спектров испускания и поглощения веществ позволяет установить энергетические уровни и тончайшие детали строения атомов. Знание же спектров атомов и молекул различных химических соединений позволяет проводить спектральный анализ, т.е. устанавливать состав исследуемых тел.

План решения задач по теме «Теория атома водорода по Бору»

1. Следует обратить внимание, что созданная Бором теория атома водорода – первая квантовая теория атома, согласно которой электрон в атоме может находиться только в определенных стационарных состояниях. Параметры электрона в атоме: радиус круговой орбиты, скорость и его момент импульса, период обращения, энергия электрона, – имеют в этих состояниях дискретные значения, которые определяются главным квантовым числом (номер орбиты). Эта зависимость отражается индексом величин: .

2. По мере увеличения номера орбиты ее радиус увеличивается , а скорость электрона уменьшается ; в результате период обращения растет , возрастает момент импульса электрона и увеличивается его энергия .

3. Порядок величин параметров электрона в атоме водорода можно оценить по указанным зависимостям и значениям величин для основного состояния . В этом состоянии радиус орбиты , скорость электрона , период обращения , момент импульса , и полная энергия электрона

Задача 30. Для электрона, находящегося на первой орбите ( ) атома водорода, определите радиус орбиты , момент импульса электрона и его скорость .

Дано Электрон в атоме : .

Решение По теории Бора электрон в атоме водорода движется по окружности радиусом . На орбите электрон удерживается кулоновской силой притяжения к ядру, имеющему положительный заряд. Эта сила создает нормальное (центростремительное) ускорение, которое, в соответствии со вторым законом Ньютона:

. (1)

Здесь – масса и скорость электрона; – заряд электрона и ядра ( ); – коэффициент пропорциональности в законе Кулона.

В уравнении (1) две неизвестные величины: . Другое уравнение, которое также содержит эти величины, – первый постулат Бора, определяющий условие квантования момента импульса электрона:

. (2)

Здесь – радиус -ой стационарной орбиты; – главное квантовое число; – постоянная Планка.

Выразим из уравнения (2) скорость электрона:

(3)

Подставим это значение скорости в уравнение (1) и определим из него радиус -ой орбиты электрона:

(4)

Полученную формулу представим в следующем виде:

, (5)

где – первый боровский радиус.

Вычисляем величину радиуса первой орбиты электрона в атоме водорода:

.

Момент импульса электрона вычисляем по уравнению (2) первого постулата Бора:

.

Скорость электрона на первой орбите в атоме водорода определим по величине момента импульса электрона (согласно уравнению (3)):

. (6)

Вычисляем скорость электрона на первой орбите в атоме водорода:

.

Задача 31. Для электрона, находящегося на третьей орбите ( ) атома водорода, определите радиус орбиты , скорость электрона на этой орбите и период его обращения .

Дано Электрон в атоме : .

Решение Запишем второй закон Ньютона для движения электрона по окружности радиусом вокруг ядра атома водорода, заряд которого (рис. 51). Сила Кулона направлена по радиусу окружности к ее центру и является центростремительной, поэтому уравнение закона Ньютона запишем в проекции на нормаль к траектории:

. (1)

Здесь – масса и скорость электрона; – заряд электрона и ядра; – кулоновская постоянная в системе единиц СИ.

Рис. 51

Так как уравнение (1) содержит две неизвестные величины: скорость движения электрона и радиус его орбиты , – то используем еще одно уравнение, которое связывает эти величины, – первый постулат Бора (условие квантования момента импульса электрона): . (2) Выразим скорость электрона из уравнения (2), подставим ее значение в уравнение (1), и определим из него радиус -ной стационарной орбиты :

. (3)

Формулу (3) представим в следующем виде:

(4)

Здесь – первый боровский радиус (согласно формуле (4) ). Вычисляем радиус третьей боровской орбиты электрона в атоме водорода:

.

Вычисляем скорость электрона на третьей орбите, используя первый постулат Бора, по формуле (3):

.

Период обращения электрона на -ной орбите: время одного оборота, – определим по формуле пути для равномерного движения электрона со скорость :

(5)

Формулу (5) представим в следующем виде:

, (6)

, – период обращения электрона на первой орбите.

Вычисляем период обращения электрона на третьей боровской орбите атома водорода по формуле (6):

.

Полученная величина периода обращения показывает, что число оборотов в одну секунду, которое совершает электрон при движении в поле ядра атома водорода: .

Задача 32. Для атома водорода определите 1) полную энергию электрона на орбитах с главным квантовым числом и 2) длину волны λ фотона, излучаемого при переходе электрона с шестого энергетического уровня на первый – в серии Лаймана (ультрафиолетовой).

Дано Электрон в атоме : ; .

Решение Полная энергия электрона в атоме водорода (и в любом другом атоме) равна сумме кинетической энергии электрона и потенциальной энергии его взаимодействия с зарядом ядра : . Таким образом, величина полной энергии атома водорода в состоянии с главным квантовым числом

. (1)

Здесь – масса электрона и его скорость на -ной орбите; – кулоновская постоянная в системе единиц СИ; – заряд электрона и ядра ; – радиус орбиты с номером .

Скорость электрона определим из закона динамики движения по круговой орбите (из второго закона Ньютона, записанного в проекции на нормаль):

. (2)

Подставим найденное значение в формулу энергии электрона (1):

(3)

Сравнивая уравнения (1) и (3), отметим соотношение энергий электрона, движущегося в атоме водорода:

1) потенциальная энергия ;

2) кинетическая энергия .

Полная энергия электрона в атоме отрицательна; это означает, что электрон находится в связанном состоянии благодаря электростатическому взаимодействию с заряженным ядром атома.

Для получения расчетной формулы полной энергии электрона в формулу (3) подставим значение радиуса орбиты ; при этом энергия электрона в состоянии с главным квантовым числом

(4)

где – энергия электрона в состоянии с квантовым числом (одна из искомых величин). Величина является минимальной энергией, которой обладает атом водорода в основном состоянии ( ). Максимальная энергия (согласно формуле (4) ) соответствует ионизации атома путем отрыва электрона от ядра.

Вычислим по формуле (4) энергию атома в возбужденном состоянии, соответствующем движению электрона по шестой стационарной орбите:

.

Чтобы определить длину волны фотона, испускаемого при переходе электрона с 6-го энергетического уровня на 1-й, используем второй постулат Бора: при переходе электрона с одной стационарной орбиты на другую излучается фотон с энергией, равной разности энергий электрона на этих орбитах:

(5)

Уравнение (5) дает следующую расчетную формулу длины волны излучаемого фотона:

(6)

Вычисляем по этой формуле длину волны спектральной линии, соответствующей переходу электрона в атоме водорода с 6-й стационарной орбиты на 1-ю (в основное состояние):

.

Это длина волны ультрафиолетового (УФ) излучения, так как величина .

План решения задач по теме «Элементы квантовой механики»

1. Длина волны де Бройля для частиц вычисляется по формуле , где импульс частицы . Если известна кинетическая энергия частицы , то импульс выражают через энергию:

Если заряженная частица (электрон, протон, -частица) ускорена электрическим полем, совершившим работу , то кинетическая энергия определяется величиной ускоряющей разности потенциалов . Привычную формулу классической механики можно использовать для частиц, кинетическая энергия которых мала по сравнению с их энергией покоя : . Приведем значения энергии покоя некоторых частиц: для электрона ; для протона ; для -частицы .

2. Длину волны де Бройля можно определить из дифракционного эксперимента, используя для параллельного пучка частиц такие же условия максимумов и минимумов дифракции, как и для потока фотонов видимого или рентгеновского излучения. Приведем эти формулы:

1) для дифракции на щели: а) условие – ;

б) условие – ;

2) для дифракции на кристалле – формула Вульфа – Брэггов:

.

3. Для микрочастиц, находящихся в ограниченной области пространства (в атоме, в ядре, в узкой потенциальной яме), характерна ненулевая минимальная кинетическая энергия: и ненулевое значение минимального импульса: , так как такая частица, согласно соотношению неопределенностей, не может иметь точные нулевые значения. Поскольку неопределенность координаты частицы , – определяется характерным размером области, то, используя соотношение , можно получить формулу, связывающую минимальную кинетическую энергию частицы с размером области: .

Задача 33. Электрон движется со скоростью . Определите длину волны де Бройля электрона, учитывая зависимость его массы от скорости.

Дано Электрон: ; ; .

Решение Длина волны де Бройля свободно движущейся частицы определяется формулой: , (1) где – постоянная Планка; – импульс частицы; – ее масса и скорость. При скоростях, сравнимых со скоростью света ,

масса частиц зависит от их скорости. Увеличение массы частицы в зависимости от ее скорости описывается формулой специальной теории относительности:

, (2)

где – масса покоя электрона; – скорость света в вакууме.

Подстановкой выражения (2) для массы электрона в формулу (1) получаем следующую расчетную формулу длины волны де Бройля релятивистского электрона:

(3)

Вычисляем величину :

.

Задача 34. Электрон прошел в электростатическом поле (ЭСП) ускоряющую разность потенциалов: 1) ; 2) . Определите длины волн де Бройля электрона при .

Дано Электрон: ; 1) ; 2) .

Решение Длина волны де Бройля свободно движущейся частицы определяется формулой: , (1) где – постоянная Планка; – импульс частицы; – ее масса и скорость.

Пройдя в ЭСП ускоряющую разность потенциалов , электрон приобрел кинетическую энергию , равную работе электрического поля:

.

Величина работы, совершенной полем, .

Приравнивая две последние формулы, определяем кинетическую энергию:

(2)

Вычисляем кинетическую энергию электрона для обоих случаев:

.

Сравним найденные величины энергии с энергией покоя электрона

.

Отмечаем, что . Следовательно, электрон не является релятивистским и для его импульса и кинетической энергии справедливы формулы классической механики:

(3)

Проверим, что это так, вычислив скорость электрона при из равенства . Релятивистская поправка (множитель) в этом случае равна .

Используя для кинетической энергии формулу (2), определяем по формуле (3) импульс электрона:

(4)

Подстановкой полученной величины импульса электрона в формулу (1) получаем следующую расчетную формулу длины волны электрона:

(5)

Вычисляем по формуле (5):

.

Вычислим величину следующим путем: согласно формуле (5)

.

Задача 35. Параллельный пучок атомов водорода, падающий под углом скольжения к поверхности монокристалла, дает дифракционный максимум 1-го порядка при отражении от плоскостей с межатомным расстоянием . Определите длину волны де Бройля атомов водорода и их скорость .

Дано Атом : ; ; ; .

Решение Для дифракции на кристалле легких частиц: электронов, - частиц, протонов, нейтронов, атомов водорода и гелия и др., – справедлива формула Вульфа – Брэггов, полученная для дифракции рентгеновских лучей (потока фотонов): (1) Осуществляя дифракцию атомов водорода на монокристалле с известным расстоянием

между атомными плоскостями, и измеряя угол скольжения для максимума 1-го порядка, по формуле (1) определяем длину волны атомов водорода:

.

Эта величина атомов водорода попадает в диапазон длин волн мягких рентгеновских лучей.

Для определения скорости атомов водорода воспользуемся формулой длины волны де Бройля свободно движущейся частицы:

, (2)

где – постоянная Планка; – импульс частицы; – ее масса и скорость.

Из этой формулы получаем расчетную формулу скорости атомов водорода и вычисляем величину :

.

Задача 36. Электрон, имеющий кинетическую энергию , находится в металлической пылинке диаметром . Оцените относительную неопределенность (точность) , с которой можно найти скорость электрона .

Дано Электрон: ; ; .

Решение Рис. 52

Электрон, находящийся внутри пылинки, движется (так как имеет энергию ) в области, ограниченной диаметром (рис. 52). При этом его координата известна с точностью до размеров пылинки, причем, (см. рис. 52). В таком случае проекция импульса электрона имеет неопределенность , величина которой следует из соотношения неопределенностей:

, (1)

где – постоянная Планка.

Неопределенность проекции импульса приводит к неопределенности проекции скорости частицы :

(2)

Используя формулу (1), определим неопределенность проекции скорости:

(3)

Чтобы найти относительную неопределенность скорости, найдем скорость электрона из его кинетической энергии:

(4)

С помощью формул (3) и (4) получаем расчетную формулу точности определения скорости электрона, находящегося в пылинке:

(5)

Здесь учтено, что величина – диаметру пылинки.

Вычисляем по формулу (5) отношение , показывающее точность определения скорости электрона:

; .

Полученная неопределенность скорости электрона в пылинке мала по сравнению с таковой для атома водорода , где . Это объясняется соотношением размеров областей, где находится электрон, и определяющих неопределенность координаты ; оно таково: ; а произведение этих неопределенностей одинаково для данной частицы (электрона): .

Задача 37. Принимая, что минимальная энергия нуклона в ядре и используя соотношение неопределенностей , оцените линейный размер ядра.

Дано Нуклон: ; ; .

Решение Нуклоном называют частицу, входящую в состав ядра – это и протон, и нейтрон. Размер ядра определяет неопределенность координаты частицы . Эту неопределенность найдем по соотношению неопределенностей:

, (1)

где – неопределенность проекции импульса нуклона.

Что известно об импульсе нуклона в ядре? В рамках капельной модели ядра нуклоны в нем колеблются (подобно колебаниям молекул в жидкости); при этом энергия нуклона, совершающего гармонические колебания, складывается из кинетической и потенциальной энергии частицы: . При прохождении нуклоном положения равновесия его потенциальная энергия , а кинетическая энергия ; соответственно

. (2)

Но кинетическая энергия частицы связана с ее импульсом формулой:

. (3)

С учетом равенства (2) получаем значение импульса нуклона:

(3а)

Таким образом, импульс нуклона известен с неопределенностью

(4)

Подстановка этой величины в формулу (1) дает расчетную формулу для оценки линейного размера атомного ядра:

. (5)

Вычисляем величину :

.

Этот результат, полученный по соотношению неопределенностей, прекрасно согласуется с экспериментальной оценкой Резерфордом размера атомных ядер: , – по рассеянию альфа-частиц металлической фольгой.

Задача 38. Время жизни возбужденного атома . С какой наименьшей погрешностью может быть определена энергия фотона, излучаемого атомом?

Дано ;

Решение Возбужденные состояния атома короткоживущие и малое время жизни приводит к заметной неопределенности энергии такого состояния: согласно соотношению неопределенностей

, (1)

где – время существования данного энергетического состояния.

Существование неопределенности означает, что энергетический уровень такого состояния имеет ширину , т. е. является размытым (рис. 53).

энергетический уровень основного состояния (   энергетический уровень возбужденного состояния ( Рис. 53

Переходы электронов в различных атомах с размытого уровня, который занимает интервал энергий от (см. рис. 53), сопровождается излучением фотонов с различной энергией – в соответствии со вторым постулатом Бора. При переходе электрона атома из одного стационарного состояния в другое (с меньшей энергией) излучается фотон, энергия которого равна разности энергий соответствующих стационарных состояний:

а) при переходе электрона с нижней границы размытого уровня на первый с энергией :

; (2)

б) при переходе электрона с верхней границы размытого уровня, где энергия атома равна :

(3)

Вычитая уравнение (2) из 3-го, получаем наибольшую разность энергий фотонов , которая вносится размытием энергетического уровня возбужденного состояния атома:

(4)

Наибольшая разность энергий фотонов , излучаемых любыми двумя одинаковыми атомами при переходе электрона , – это и есть неопределенность энергии излучаемого фотона. Эта неопределенность, с учетом формулы (1):

(5)

Оценим ее величину:

.

Задача 39. Атом испустил фотон с длиной волны . Длительность излучения . Определите наибольшую точность , с которой может быть измерена длина волны излучения.

Дано ; . ?

Решение В соответствии с соотношением неопределенностей уровень энергии возбужденного состояния атома имеет ненулевую ширину : , (1) где – неопределенность энергии атома в возбужденном

состоянии, равная ширине этого размытого уровня энергии (см. рис. 53); – время существования данного возбужденного состояния.

При переходах электронов в различных атомах с разных по высоте точек, находящихся в зоне возбужденного уровня, излучаются фотоны с энергией, лежащей в интервале от , частота которых находится в области от , (см. рис. 53). Запишем формулу Планка для энергии этих фотонов:

; (2)

(3)

Оценим неопределенность частоты излучаемых фотонов, вычитая уравнение (2) из уравнения (3):

(4)

Используя соотношение неопределенностей (1), определим ширину данной спектральной линии по шкале частот:

(5)

Относительная ширина спектральной линии

. (6)

Вычисляем:

Покажем, что относительная ширина спектральной линии одинакова как по шкале частот, так и по длинам волн, т. е. . Так как, согласно сделанному выше расчету, , т. е. величина , то можно отождествить измеряемый разброс по частотам с бесконечно малым приращением : . Дифференцируем формулу связи длины волны и частоты :

. (7)

Следовательно, монохроматичность спектральной линии, или ее относительная ширина . Знак в формуле (7) опущен, так как он указывает только на то, что с увеличением частоты света убывает его длина волны .

Постулаты Бора. Первый постулат:в атоме существуют стационарные (не изменяющиеся со временем) состояния, находясь в которых атом не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, на которых находятся электроны. В стационарном состоянии атома для электрона на круговой орбите значения момента импульса могут принимать только определенный набор дискретных значений, удовлетворяющих условию:

( n = 1, 2, 3, …), где

m_e –масса электрона, υ_n – скорость электрона на n-ой орбите радиуса r_n,

n – номер орбиты, ħ = h/2 (h – постоянная Планка).

Радиус n-ой орбиты для атома водорода: , где

где e – заряд электрона, ε_o – электрическая постоянная,

а – радиус первой орбиты ( n = 1), называемый первым боровским радиусом.

Второй постулат:при переходе электрона с одной стационар­ной орбиты на другую излучается (или поглощается) один фотон с энергией hν, равной разности энергий соответствующих стационарных состояний E_n и Е_m :

.

При переходе атома из состояния большей энергии в состояние меньшей энергии происходит излучение фотона, а при поглощении фотона происходит переход атома из состояния меньшей энергии в состояние большей энергии.

Дискретность набора значений энергии стационарных состояний E_n и Е_m предопределяет дискретность набора возможных частот ν квантовых переходов между этими состояниями, что обусловливает линейчатость спектра атома.

По теории Бора полная энергия электрона на n-ой орбите атома водорода:

( n = 1, 2 , 3, …),

Из приведенной формулы следует, что энергетические состояния атома образуют после­довательность уровней, энергия которых изменяется в зависимости от значения числа n , называемое главным квантовым числом. Энергетическое состояние с n = 1 является основнымсостоянием, а состояния с n >1 являются возбужденными состояниями.

Согласно второму постулату Бора, при переходе атома водорода из состояния n в состоя­ние т с меньшей энергией испускается фотон с энергией hν :

,

откуда частота ν квантового перехода в спектре испускания атома водорода:

, где R – постоянная Ридберга ( ) .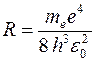

Числа m (m = 1, 2, 3 …) и n (n = m + 1, m + 2, m + 3, …) определяют номера электронных орбит в атоме, между которыми происходит квантовый переход.

Приведенная формула описывает серии линий в спектре испускания атома водорода (рис. 31), где m определяет серию (m = 1, 2, 3…), а n определяет отдельные линии соответствующей серии (n = m + 1, m + 2, m + 3, …).

Спектр испускания атома водорода.

В ультрафиолетовой области спектра атома водорода наблюдается

серия Лаймана (m = 1): (n = 2, 3, 4, …).

В видимой области спектра атома водорода наблюдается

серия Бальмера (m = 2): (n = 3, 4, 5, …).

В инфракрасной области спектра атома водорода наблюдаются:

серия Пашена (m = 3): (n = 4, 5, 6, …);

серия Брэкета (m = 4): (n = 5, 6, 7, …);

серия Пфунда (m = 5): (n = 6, 7, 8, …);

серия Хэмфри (m = 6): (n = 7, 8, 9, …).

Рис. 31.

Таким образом, квантовая теория атома, созданная Бором, позволила описать экспериментально наблюдаемые атомные спектры поглощения и испускания.

Атом водорода. Линейчатые спектры

Простейший из атомов, атом водорода явился своеобразным тест-объектом для теории Бора. Ко времени создания теории он был хорошо изучен экспериментально. Было известно, что он содержит единственный электрон. Ядром атома является протон – положительно заряженная частица, заряд которой равен по модулю заряду электрона, а масса в 1836 раз превышает массу электрона. Еще в начале XIX века были открыты дискретные спектральные линии в видимой области излучения атома водорода (так называемый линейчатый спектр). Впоследствии закономерности, которым подчиняются длины волн (или частоты) линейчатого спектра, были хорошо изучены количественно (И. Бальмер, 1885 г.). Совокупность спектральных линий атома водорода в видимой части спектра была названа серией Бальмера. Позже аналогичные серии спектральных линий были обнаружены в ультрафиолетовой и инфракрасной частях спектра. В 1890 году И. Ридберг получил эмпирическую формулу для частот спектральных линий:

Для серии Бальмера m = 2, n = 3, 4, 5, ... . Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4, ... . Постоянная R в этой формуле называется постоянной Ридберга. Ее численное значение R = 3,29·10¹⁵ Гц. До Бора механизм возникновения линейчатых спектров и смысл целых чисел, входящих в формулы спектральных линий водорода (и ряда других атомов), оставались непонятными.

Постулаты Бора определили направление развития новой науки – квантовой физики атома. Но они не содержали рецепта определения параметров стационарных состояний (орбит) и соответствующих им значений энергии E_n.

Правило квантования, приводящее к согласующимся с опытом значениям энергий стационарных состояний атома водорода, Бором было угадано. Он предположил, что момент импульса электрона, вращающегося вокруг ядра, может принимать только дискретные значения, кратные постоянной Планка. Для круговых орбит правило квантования Бора записывается в виде

Здесь m_e – масса электрона, υ – его скорость, r_n – радиус стационарной круговой орбиты. Правило квантования Бора позволяет вычислить радиусы стационарных орбит электрона в атоме водорода и определить значения энергий. Скорость электрона, вращающегося по круговой орбите некоторого радиуса r в кулоновском поле ядра, как следует из второго закона Ньютона, определяется соотношением

где e – элементарный заряд, ε₀ – электрическая постоянная. Скорость электрона υ и радиус стационарной орбиты r_n связаны правилом квантования Бора. Отсюда следует, что радиусы стационарных круговых орбит определяются выражением

Самой близкой к ядру орбите соответствует значение n = 1. Радиус первой орбиты, который называется боровским радиусом, равен

Радиусы последующих орбит возрастают пропорционально n².

Полная механическая энергия E системы из атомного ядра и электрона, обращающегося по стационарной круговой орбите радиусом r_n, равна

Следует отметить, что E_p < 0, так как между электроном и ядром действуют силы притяжения. Подставляя в эту формулу выражения для υ² и r_n, получим:

Целое число n = 1, 2, 3, ... называется в квантовой физике атома главным квантовым числом.

Согласно второму постулату Бора, при переходе электрона с одной стационарной орбиты с энергией E_n на другую стационарную орбиту с энергией E_m < E_n атом испускает квант света, частота ν_nm которого равна ΔE_nm / h:

Эта формула в точности совпадает с эмпирической формулой Ридберга для спектральных серий атома водорода, если положить постоянную R равной

Подстановка числовых значений m_e, e, ε₀ и h в эту формулу дает результат

R = 3,29·1015 Гц,

который очень хорошо согласуется с эмпирическим значением R. Рис. 6.3.1 иллюстрирует образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.

Рисунок 6.3.1. Стационарные орбиты атома водорода и образование спектральных серий

На рис. 6.3.2. изображена диаграмма энергетических уровней атома водорода и указаны переходы, соответствующие различным спектральным сериям.

Рисунок 6.3.2. Диаграмма энергетических уровней атома водорода. Показаны переходы, соответствующие различным спектральным сериям. Для первых пяти линий серии Бальмера в видимой части спектра указаны длины волн

Прекрасное согласие боровской теории атома водорода с экспериментом служило веским аргументом в пользу ее справедливости. Однако попытки применить эту теорию к более сложным атомам не увенчались успехом. Бор не смог дать физическую интерпретацию правилу квантования. Это было сделано десятилетием позже де Бройлем на основе представлений о волновых свойствах частиц. Де Бройль предложил, что каждая орбита в атоме водорода соответствует волне, распространяющейся по окружности около ядра атома. Стационарная орбита возникает в том случае, когда волна непрерывно повторяет себя после каждого оборота вокруг ядра. Другими словами, стационарная орбита соответствует круговой стоячей волне де Бройля на длине орбиты (рис. 6.3.3). Это явление очень похоже на стационарную картину стоячих волн в струне с закрепленными концами.

Рисунок 6.3.3. Иллюстрация идеи де Бройля возникновения стоячих волн на стационарной орбите для случая n = 4

В стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться по идее де Бройля целое число длин волн λ, т. е.

nλn = 2πrn.

Подставляя в это соотношение длину волны де Бройля λ = h / p, где p = m_eυ – импульс электрона, получим:

Таким образом, боровское правило квантования связано с волновыми свойствами электронов.

Успехи теории Бора в объяснении спектральных закономерностей в изучении атома водорода были поразительны. Стало ясно, что атомы – это квантовые системы, а энергетические уровни стационарных состояний атомов дискретны. Почти одновременно с созданием теории Бора было получено прямое экспериментальное доказательство существования стационарных состояний атома и квантования энергии. Дискретность энергетических состояний атома была продемонстрирована в 1913 г., в опыте Д. Франка и Г. Герца, в котором исследовалось столкновение электронов с атомами ртути. Оказалось, что если энергия электронов меньше 4,9 эВ, то их столкновение с атомами ртути происходит по закону абсолютно упругого удара. Если же энергия электронов равна 4,9 эВ, то столкновение с атомами ртути приобретает характер неупругого удара, т. е. в результате столкновения с неподвижными атомами ртути электроны полностью теряют свою кинетическую энергию. Это означает, то атомы ртути поглощают энергию электрона и переходят из основного состояния в первое возбужденное состояние,

E2 – E1 = 4,9 эВ.

Согласно боровской концепции, при обратном самопроизвольном переходе атома ртуть должна испускать кванты с частотой

Спектральная линия с такой частотой действительно была обнаружена в ультрафиолетовой части спектра излучения атомов ртути.

Представление о дискретных состояниях противоречит классической физике. Поэтому возник вопрос, не опровергает ли квантовая теория ее законы.

Квантовая физика не отменила фундаментальных классических законов сохранения энергии, импульса, электрического разряда и т. д. Согласно сформулированному Н. Бором принципу соответствия, квантовая физика включает в себя законы классической физики, и при определенных условиях можно обнаружить плавный переход от квантовых представлений к классическим. Это можно видеть на примере энергетического спектра атома водорода (рис. 6.3.2). При больших квантовых числах n >> 1 дискретные уровни постепенно сближаются, и возникает плавный переход в область непрерывного спектра, вытекающего из классической физики.

Половинчатая, полуклассическая теория Бора явилась важным этапом в развитии квантовых представлений, введение которых в физику требовало кардинальной перестройки механики и электродинамики. Такая перестройка была осуществлена в 20-е – 30-е годы XX века.

Представление Бора об определенных орбитах, по которым движутся электроны в атоме, оказалось весьма условным. На самом деле движение электрона в атоме очень мало похоже на движение планет или спутников. Физический смысл имеет только вероятность обнаружить электрон в том или ином месте, описываемая квадратом модуля волновой функции |Ψ|². Волновая функция Ψ является решением основного уравнения квантовой механики – уравнения Шредингера. Оказалось, что состояние электрона в атоме характеризуется целым набором квантовых чисел. Главное квантовое число n определяет квантование энергии атома. Для квантования момента импульса вводится так называемое орбитальное квантовое число l. Проекция момента импульса на любое выделенное в пространстве направление (например, направление вектора магнитного поля) также принимает дискретный ряд значений. Для квантования проекции момента импульса вводится магнитное квантовое число m. Квантовые числа n, l, m связаны определенными правилами квантования. Например, орбитальное квантовое число l может принимать целочисленные значения от 0 до (n – 1). Магнитное квантовое число m может принимать любые целочисленные значения в интервале ±l. Таким образом, каждому значению главного квантового числа n, определяющему энергетическое состояние атома, соответствует целый ряд комбинаций квантовых чисел l и m. Каждой такой комбинации соответствует определенное распределение вероятности |Ψ|² обнаружения электрона в различных точках пространства («электронное облако»).

Состояния, в которых орбитальное квантовое число l = 0, описываются сферически симметричными распределениями вероятности. Они называются s-состояниями (1s, 2s, ..., ns, ...). При значениях l > 0 сферическая симметрия электронного облака нарушается. Состояния с l = 1 называются p-состояниями, с l = 2 – d-состояниями и т. д.

На рис. 6.3.4 изображены кривые распределения вероятности ρ (r) = 4πr²|Ψ|² обнаружения электрона в атоме водорода на различных расстояниях от ядра в состояниях 1s и 2s.

Рисунок 6.3.4. Распределение вероятности обнаружения электрона в атоме водорода в состояниях 1s и 2s. r1 = 5,29·10–11 м – радиус первой боровской орбиты

Как видно из рис. 6.3.4, электрон в состоянии 1s (основное состояние атома водорода) может быть обнаружен на различных расстояниях от ядра. С наибольшей вероятностью его можно обнаружить на расстоянии, равном радиусу r₁ первой боровской орбиты. Вероятность обнаружения электрона в состоянии 2s максимальна на расстоянии r = 4r₁ от ядра. В обоих случаях атом водорода можно представить в виде сферически симметричного электронного облака, в центре которого находится ядро.

Модель. Квантование электронных орбит

Модель. Атом водорода

Модель. Частица в потенциальной яме

Модель атома водорода по Бору

Исходя из этих постулатов и используя планетарную модель строения атома, Н. Бор разработал количественную теорию атома водорода. Он рассчитал радиусы стационарных орбит электрона в атоме водорода и вычислил соответствующие им значения энергии.

Расчет радиусов орбит.' Электрон движется вокруг ядра в атоме водорода по круговой орбите под действием кулоновской силы, которая сообщает

ему центростремительное ускорение. По второму закону Ньютона F⃗=ma⃗.F→=ma→.

Центростремительное ускорение acs=υ2racs=υ2r электрону сообщает кулоновская сила притяжения со стороны ядра F=e24πε0r2.F=e24πε0r2. Следовательно,

mυ2r=e24πε0r2,mυ2r=e24πε0r2, откуда mυ2=e24πε0r2.mυ2=e24πε0r2. (20.1)

Согласно III постулату Бора

mυr=nh2π,mυr=nh2π,

отсюда

υ=nh2πmr.υ=nh2πmr. (20.2)

Из уравнений (20.1) и (20.2) получим mn2h24π2m2r2=e24πε0r2v.mn2h24π2m2r2=e24πε0r2v.

Откуда

r=n2h2ε0πme2—r=n2h2ε0πme2— (20.3)

выражение для радиусов разрешенных стационарных орбит электрона в атоме водорода. Здесь n — номер орбиты, радиус которой r, ε0ε0 — электрическая постоянная, h — постоянная Планка, m — масса электрона, е — заряд электрона.

Мы видим, что радиусы стационарных устойчивых орбит возрастают пропорционально квадратам номеров орбит (рис. 20.3)

 r1:r2:r3⋯=12:22:32 r1:r2:r3⋯=12:22:32

и т.д. Если электрон в атоме водорода находится на одной из стационарных орбит, то атом обладает определенным значением энергии, определяемой энергией электрона:

W=Wk+Wn=mυ22−e24πε0r2v.W=Wk+Wn=mυ22−e24πε0r2v.

(Знак "-" перед потенциальной энергией означает, что за  Wn=0 Wn=0 принято то значение, которое соответствует  r=∞ r=∞ ). Подставив в эту формулу значения  υ υ и r из формул (20.2) и (20.3), получим:

W=m2n2h24π2m2r2−e24πε0r2=n2h2π2m2e28π2mn4h4ε20−e2πme24πε0n2h2ε0=me48πε0vn2h2.W=m2n2h24π2m2r2−e24πε0r2=n2h2π2m2e28π2mn4h4ε02−e2πme24πε0n2h2ε0=me48πε0vn2h2.

Таким образом, энергия электрона, находящегося на n-й орбите,

W=−me48πε0vn2h2.W=−me48πε0vn2h2. (20.4)

Из этой формулы видно, что значения энергии атома водорода квантованы и, чем больше n, тем больше энергия W_n. Для наглядного представления возможных энергетических состояний атомов используются энергетические диаграммы, на которых каждое стационарное состояние атома отмечается горизонтальной линией, называемой энергетическим уровнем (рис. 20.4). Ниже всех на диаграмме располагается энергетический уровень, соответствующий основному состоянию (состояния с минимальной энергией). Энергетические уровни возбужденных состояний располагаются над основным уровнем на расстояниях, пропорциональных разности энергий возбужденного и основного состояний. Переходы атома из одного состояния в другое изображаются вертикальными линиями между соответствующими уровнями на диаграмме. Направление перехода обозначается стрелкой. При переходе электрона с k-й на n-ю орбиту излучается фотон с частотой

νkn=Wk−Wnh=me48ε20h3(1n2−1k2).νkn=Wk−Wnh=me48ε02h3(1n2−1k2).

Рис. 20.4

Сравнивая это выражение с эмпирической формулой

νkn=R(1n2−1k2),νkn=R(1n2−1k2), (20.5)

видим, что постоянная Ридберга R=me48ε20h3;R=me48ε02h3; следовательно, в формуле (20.5) k — номер орбиты, с которой происходит переход электрона в атоме, n — номер орбиты, на которую переходит электрон