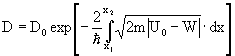- •Раздел 7
- •Глава 23
- •§ 23.1. Гипотеза де Бройля.
- •§ 23.2. Электронный микроскоп. Понятие об электронной оптике
- •§ 23.3. Волновая функция и её физический смысл
- •§ 23.4. Соотношения неопределенностей
- •§ 23.5. Уравнение Шредингера.
- •28.1. Гипотеза де бройля. Опыты по дифракции электронов и других частиц
- •28.2. Электронный микроскоп. Понятие об электронной оптике
- •28.3. Волновая функция и ее физический смысл
- •28.4. Соотношения неопределенностей
- •28.5. Уравнение шредингера. Электрон в потенциальной яме
- •28.6. Применение уравнения шредингера к атому водорода. Квантовые числа
- •28.7. Понятие о теории бора
- •28.8. Электронные оболочки сложных атомов
- •28.9. Энергетические уровни молекул
Гипотеза Де Бройля. Электронная микроскопия. Волновая функция.
Волны де Бройля
В начале XX века картина мира выглядела очень чётко и не представляла вариантов для толкования:
|
Каких частиц — это отдельный вопрос. Но именно так: или частицы или волна — и никак иначе! Всё ясно и понятно.
Такая идиллия продолжалась до 1924 года, пока французский физик Луи де Бройль не пришёл к выводу, что волновые свойства присущи абсолютно всем материальным объектам.
|
На эту гипотезу де Бройля натолкнуло сходство уравнений, описывающих поведение лучей света методами геометрической оптики, и движение частиц в механике методом уравнений Гамильтона.
Предположение было неожиданным, красивым и многое объясняло, но нужно было его экспериментальное подтверждение, иначе всё так и осталось бы на уровне гипотезы.
Первое экспериментальное подтверждение гипотезы де Бройля в 1927 году получили американские исследователи Дэвидсон и Джермер. Они изучали угловое распределение электронов, рассеивающихся на монокристалле никеля.
|
Схема эксперимента представлена на рис.1. Испускаемые нитью накала 1 термоэлектроны проходят ускоряющую разность потенциалов U в поле, создаваемом между электродами 1 и 2. После вылета из отверстия в электроде 2 и прохождения набора диафрагм узкий пучок разогнанных электронов попадал на монокристалл никеля 3, на котором и происходило рассеяние. |
Ионизационной
камерой 4,
с присоединённым с ней гальванометром
5,
по силе возникающего тока I
измерялось число электронов, отражённых
от кристалла под углом
![]() ,
равным углу падения, то есть — интенсивность
отражённого электронного пучка.
,
равным углу падения, то есть — интенсивность
отражённого электронного пучка.
|
В результате измерений было обнаружено два очень примечательных факта:
|
Если же угол падения электронного пучка на кристалл менялся, а ускоряющее напряжение U оставалось неизменным, то интенсивность отражённого пучка имела ярко выраженные максимумы при углах падения, удовлетворяющих условию Вульфа-Брэгга.
Способ нахождения импульса зависит от скорости, которую имеет частица. Если скорость движения частицы во много раз меньше скорости света в вакууме, то импульс (количество движения) определяется привычной формулой.
|
(2) |
Здесь m0 — масса покоя частицы, v — её скорость.
При скоростях же, близких к скорости света, импульс является более сложной функцией
|
(3) |
Выясним, какое выражение (2 или 3) надо использовать для нахождения импульса в данном случае. Для этого сравним энергию электронов в условиях опыта Дэвидсона и Джермера с их энергией покоя.
В
проведённых экспериментах ускоряющее
напряжение было на уровне 400В.
В этом случае энергия электронов не
превышала Ee=
eU = 400 эВ.
Энергия же покоя электрона Eo=
mo![]() c2
= 0,511 МэВ = 511000 эВ.
Следовательно, Ee<<
Eo,
электроны являются нерелятивистскими
и для нахождения их импульса можно
использовать выражение (2).
c2
= 0,511 МэВ = 511000 эВ.
Следовательно, Ee<<
Eo,
электроны являются нерелятивистскими
и для нахождения их импульса можно
использовать выражение (2).
При разгоне (ускорении) электрона работа сил электрического поля идёт на увеличение его кинетической энергии. Для условий эксперимента получаем
|
(2) |
Отсюда
находим, что
![]() .
Тогда для опыта Дэвидсона
и Джермера
длина волны де
Бройля
может быть записана как
.
Тогда для опыта Дэвидсона
и Джермера
длина волны де
Бройля
может быть записана как
|
(3) |
Подстановка числовых значений даёт
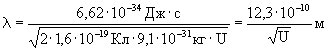
Следовательно, при U = 400 В в описываемых экспериментах имеем для электрона значение длины волны де Бройля равное = 6,2 10-11м.
Такое же значение для длины волны дал и расчёт по формуле Вульфа-Брэгга, основанной на волновой теории.
Гипотеза Луи де Бройля о наличии у частиц волновых свойств получила своё экспериментальное подтверждение.
Вроде бы можно успокоиться и заняться чем-либо другим. Однако вопрос, поднятый де Бройлем, был слишком фундаментальным и нужны были более наглядные подтверждения. Поэтому экспериментаторы продолжили свою работу.
Следует отметить, что одновременно и независимо от Дэвидсона этими вопросами занимался профессор Абердинского университета Джордж П.Томсон (сын знаменитого Джозефа Джона Томсона, открывшего электрон), который и добился успеха первым.
|
В своих экспериментах вместо пучка медленных электронов, который трудно было регулировать, Дж.Томсон использовал пучок быстрых электронов, создаваемых катодной трубкой. Вместо отражения от толстой пластинки (кристалла) он исследовал прохождение электронов через тонкую фольгу, а для регистрации результатов вместо гальванометра взял фотографическую пластинку. Для устранения рассеяния электронов на молекулах воздуха установка тщательно откачивалась ртутными насосами. |
На рис. 3 приведены первые фотографии с двумя дифракционными картинами при разных напряжениях на катодной трубке. Видно, что увеличение напряжения (левый снимок), приводящее к увеличению энергии электронов, приводит и к более чёткой картине с большим числом колец.
Многократно повторив свои эксперименты с различными образцами фольги, Джордж П.Томсон пришёл к выводу:
|
Несколько после Дж.П.Томсона аналогичные результаты были получены П.С.Тартаковским, а затем и другими физиками, которые также смогли зафиксировать дифракционные кольца, возникающие при прохождении пучка электронов через тонкие слои металла.
Советский физик Иосив Мандельштам с сотрудниками пошёл ещё дальше, он сумел экспериментально показать, что де Бройлевские волны могут интерферировать между собой.
Затем был показано, что волновые свойства обнаруживают нейтроны, протоны и даже молекулы водорода.
Дифракция электронов (электронография) применяется сейчас при исследовании структуры поверхности, например, при изучении коррозии, при адсорбции газов на поверхностях.
Дифракция нейтронов (нейтронография) является мощным средством изучения структур, в особенности органических кристаллов, содержащих водород, что невозможно сделать с использованием рентгеновского излучения.
Появились
и новая отрасль науки — электронная
оптика,
давшая миру новый прибор — электронный
микроскоп,
без которого в настоящее время немыслимы
многие исследования. При ускоряющих
напряжениях от 50
до 100
кВ
разрешающая
способность электронных микроскопов
приближается к 20
![]() .
.
Но всё это было позже, а первопроходцы
Дэвидсон и Томсон за свои эпохальные эксперименты в 1937 году были удостоены Нобелевской премии по физике. |
![]()
Соотношение неопределённости Гейзенберга
Доказанное одновременное наличие у микрочастиц и корпускулярных и волновых свойств приводило к невозможности применения к ним законов классической механики.
В макромире можно однозначно определить в любой момент времени импульс и координату движущего тела или материальной точки; можно рассчитать и траекторию их движения.
В микромире из-за наличия волновых свойств одновременные значения координат и скорости (импульса) не существуют: если известна скорость (импульс), то местоположение частицы (её координаты) не имеют определённого значения — понятие длина волны в конкретной точке не имеет смысла. То же самое и наоборот.
Налицо парадокс, который впервые был сформулирован немецким физиком Вернером Гейзенбергом в виде так называемого принципа неопределённости:
|
||||
Разделив выражение (4) на массу m частицы, получим другую форму записи принципа неопределённости:
|
(5) |
То есть, чем точнее определена скорость частицы вдоль оси х (то есть чем меньше vx), тем больше неопределённость её координаты (то есть тем больше х).
Причём эта неопределённость обусловлена не грубостью приборов, а самой природой исследуемых тел (частиц). |
Сказанное выше хорошо иллюстрируется несколькими примерами, с которыми можно познакомиться здесь.
Если выразить pх через энергию ( pх = Е/ vx), то учитывая, что х/ vх= t, получаем соотношение неопределённостей для энергии E и времени t:
|
(6) |
Здесь
t
представляет
собой время, в течение которого
микрочастица обладает энергией
![]() .
.
Например,
атом на самом
низком энергетическом уровне
может пребывать сколь угодно долго (![]() ),
поэтому энергия этого состояния вполне
определена:
Е
= 0.
),
поэтому энергия этого состояния вполне
определена:
Е
= 0.
В
более
высоком энергетическом состоянии
атом пребывает очень недолго. Если это
время равно
t,
то энергия атома в этом состоянии может
быть определена с точностью до
![]() и
будет равна
.
При переходе атома с более высокого
уровня на более низкий энергетический
уровень с энергией Е' он излучает фотон
с энергией
и
будет равна
.
При переходе атома с более высокого
уровня на более низкий энергетический
уровень с энергией Е' он излучает фотон
с энергией
|
(7) |
Таким образом, энергия излучённого фотона может быть известна только с точностью до Е. Величина же Е определяется временем t жизни атома в возбуждённом состоянии.
На
основании выражения (7) можно утверждать,
что частота
излучённого кванта
(фотона) имеет
неопределённость,
равную
![]() =
Е
/ h, то есть линии в спектре будут иметь
частоту, равную
=
Е
/ h, то есть линии в спектре будут иметь
частоту, равную
![]() Е
/ h.
Е
/ h.
Именно это и наблюдается на опыте: |
|
|
Уравнение Шредингера
В классической механике движение любой материальной точки однозначно описывается уравнением Исаака Ньютона (второй закон Ньютона), которое в движении вдоль оси ОХ (одномерный случай) имеет вид
|
|
|
(8) |
В квантовой механике необходим учёт волновых свойств частиц. Поэтому вместо формулы (8) должно быть использовано другое уравнение. Такое уравнение в 1926 году было записано Эрнестом Шредингером и носит его имя.
Чтобы уравнение, описывающее движения микрочастицы, учитывало её волновые свойства, это уравнение должно быть волновым. Для плоской волны, распространяющейся вдоль оси ОХ, волновое уравнение представляет собой дифференциальное уравнение второго порядка в частных производных. Независимыми переменными в нём являются координата и время.
В случае электромагнитной волны имеем
|
|
|
(9) |
где |
|
|
E и H — напряжённости электрического и магнитного полей волны, v — скорость распространения волны. |
Для
описания движения микрочастицы введём
функцию
![]() =
(x,
y, z, t),
связанную с длиной
волны де Бройля
(смысл этой функции рассмотрим ниже). В
этих обозначениях получим
=
(x,
y, z, t),
связанную с длиной
волны де Бройля
(смысл этой функции рассмотрим ниже). В
этих обозначениях получим
|
|
|
(10) |
где v — скорость распространения волны де Бройля.
Решением этого уравнения будет уравнение бегущей волны, распространяющейся вдоль оси ОХ
|
(11) |
Возьмём вторую частную производную уравнения (11) по времени, то есть продифференцируем его два раза по t
|
|
|
(12) |
Полученный в (12) результат подставим в волновое уравнение (10)
|
|
|
(13) |
Поскольку v/ = , то можем записать ( /v)2 =1/( )2. Теперь, зная, что длина волны де Бройля = h/(mv), получим
|
|
( /v)2 = (mv)2/(h)2. |
(14) |
Далее имеем
(mv)2 = 2m(mv)2/2 = 2mWкин = 2m(E - U), |
(15) |
где |
||
|
E Wкин U |
— полная, — кинетическая, — потенциальная энергия частицы. |
С учётом (14) и (15) из (13) получаем
|
|
|
|
(16) |
Уравнение (16) называется одномерным стационарным уравнением Шредингера.
В случае движения частицы в любом (не только по оси ОХ) направлении, то уравнение (16) принимает вид
|
|
|
|
(17) |
Здесь
![]() —
оператор Лапласа. Применение его к
пси-функции даёт
—
оператор Лапласа. Применение его к
пси-функции даёт
![]() —
лаплассиан
.
—
лаплассиан
.
В общем случае волновое уравнение является функцией двух видов переменных. Как уже говорилось, уравнение Шредингера в виде (16) и (17) не зависит от времени и записано для стационарного случая, при котором волновая функция не зависит от времени: в уравнении (16) = (x), а в уравнении (17) = (x, y, z).
При учёте времени как ещё одной переменной, = (x, y, z, t) и уравнение Шредингера принимает вид
|
|
|
|
(18) |
В
виде (18) уравнение получило название
временн![]() го
уравнения Шредингера.
го
уравнения Шредингера.
Во-первых, оно справедливо лишь при малых (по сравнению со скоростью света в вакууме) скоростях движения частицы, когда v<< c. Во-вторых, уравнение Шредингера не описывает процессы, происходящие с изменением числа взаимодействующих частиц, их рождением или аннигиляцией, и не учитывает внутренних степеней свободы частиц, таких, например, как спин. |
Релятивистский
вариант этого уравнения (когда v
![]() c.)
был получен Полем
Дираком
(здесь мы его не рассматриваем).
c.)
был получен Полем
Дираком
(здесь мы его не рассматриваем).
Записанные выше (16) и (17) стационарные варианты уравнения Шредингера получаются из временн го уравнения (18) при не учёте фактора времени.
|
Уравнение Шредингера записано для частицы, движущейся в поле, характеризуемом потенциальной энергией U. При решении этого уравнения надо задать вид потенциального поля и закон изменения U. Из решения этого уравнения следует закон квантования энергии для частиц, совпадающий с правилами, введёнными Бором при разработке теории атома водорода. Однако здесь он получается естественным путём, как результат решения, а не искусственно постулируется, как у Бора.
Приведённые в этом разделе рассуждения не претендуют на вывод уравнения Шредингера. По сути, уравнение (18) постулируется, а об его справедливости судят, сравнивая следствия из этого уравнения с результатами экспериментов.
Именно благодаря экспериментальным свидетельствам и можно с уверенностью утверждать, что уравнение Шредингера успешно описывает поведение микрообъектов в нерелятивистском приближении.
Допустим, что имеется столь слабый поток частиц, что сквозь щель проходит один электрон за другим через большой промежуток времени. Уравнение Шредингера не позволяет точно предсказать, в какое именно место экрана попадёт конкретный электрон. Это уравнение даёт только вероятность распределения частиц по экрану после прохождения щели. Однако, если эксперимент продолжать достаточно долго, так, чтобы на экран попало большое количество частиц, возникает обычная дифракционная картина.
|
На рис. 5 приведены результаты расчёта по уравнению Шредингера дифракции такого слабого пучка электронов на одной щели (сплошная синяя линия). На неё наложена ступенчатая кривая, показывающая распределение отдельных частиц, регистрируемых чувствительным счётчиком. |
Следовательно, теория предсказывает только статистический результат, то есть то, что произойдёт в среднем, за большой промежуток времени.
Волновая функция
Попробуем теперь разобраться, что представляет собой введённая в предыдущем параграфе волновая функция = (x, y, z, t),.
|
|
Рис. 4. Распространение плоского волнового фронта |
|
=
|
(19) |
где
0 —
амплитуда,
—
частота, t
— время. Через некоторое время ![]() фронт волны переместится и займёт
положение A'B'.
фронт волны переместится и займёт
положение A'B'.
Колебания в плоскости этого нового волнового фронта выразятся формулой
= 0 exp[ -2 i (t - )]. |
(20) |
Будем отсчитывать от точки О расстояние r в некотором произвольном направлении, составляющем угол с нормалью On. Тогда
|
(21) |
Здесь |
|
|
|
Подставив это значение в (21) и приняв во внимание, что = v/ , получим
|
(22) |
Применим это выражение для описания пучка частиц, характеризующихся длиной волны де Бройля.
Направление
нормали
совпадает
с направлением скорости частиц v,
таким образом,
![]() окажется
равным
окажется
равным
|
(23) |
где
![]() —
вектор количества движения.
—
вектор количества движения.
Далее воспользуемся оптической аналогией. Выражение (23) кроме длины волны содержит и частоту . В квантовой теории частота кванта связана с его энергией соотношением Е = h . По аналогии с этим положим, что частота связана с энергией частицы W выражением = W/h.
Тогда для волны, характеризующей пучок частиц постоянной скорости, из (22) и учётом (23) получим
|
(24) |
|
||
|
Примечание

Чтобы привести экспоненциальную форму представления волновой функции в тригонометрическую воспользуемся формулами Эйлера. Для этого перепишем (24) в виде
![]()
Отсюда по Эйлеру получаем
![]()
Ограничившись
действительной частью, переходя к
одномерному случаю и учитывая, что
![]() ,
окончательно получаем
,
окончательно получаем
|
(24') |
Выражение (24' ) полностью совпадает с выражением (11), использованном выше при выводе уравнения Шредингера.
В квантовой механике волновая -функция полностью описывает все свойства частицы, но, как это ни может показаться странным, сама по себе волновая функция физического смысла НЕ имеет.
|
|
Таким образом, вероятность dw того, что частица при измерении находится в объёме dV около точки с координатами (x, y, z) , равна
|
|
|
|
(25) |
Чтобы волновая функция являлась объективной характеристикой микрочастицы она должна удовлетворять следующим условиям:
|
|
|
Такая трактовка свойств волновой функции принадлежит немецкому физику Максу Борну и подтверждена огромным количеством экспериментов.
Электрон в потенциальной яме
Р ассмотрим
электрон, находящийся в так называемой
"потенциальной
яме".
Под эти понимается, что на отрезке 0
< х < а
(внутри ямы или, как ещё иногда говорят,
ящика)
потенциальная энергия энергия электрона
неизменна и конечна, например, равна
нулю (U(x)
= 0),
а
вне этого отрезка при х
< 0
и х>
а
и на его границах при х
= 0
и х
= а
потенциальная энергия обращается в
бесконечность.
ассмотрим
электрон, находящийся в так называемой
"потенциальной
яме".
Под эти понимается, что на отрезке 0
< х < а
(внутри ямы или, как ещё иногда говорят,
ящика)
потенциальная энергия энергия электрона
неизменна и конечна, например, равна
нулю (U(x)
= 0),
а
вне этого отрезка при х
< 0
и х>
а
и на его границах при х
= 0
и х
= а
потенциальная энергия обращается в
бесконечность.
При описанных условиях одномерное стационарное уравнение Шредингера (16) можно записать в виде
![]()
Поскольку потенциальная энергия по условию равна нулю, то полная энергия Е в этом уравнении равна кинетической энергии частицы (электрона).
Конечно символика частной производной здесь лишняя, но не будем ничего менять, просто помним, что зависит только от одной переменной — х.
Преобразуем множитель перед -функцией:
|
(27) |
Тогда получаем
|
(28) |
Здесь
![]() —
не что иное, как длина волны де Бройля
для электрона.
—
не что иное, как длина волны де Бройля
для электрона.
Решения уравнения (28) будут иметь вид
1) |
|
(29) |
2) |
|
(30) |
По условию частица не может находиться вне ящика, поэтому её волновая функция на границах ящика при х = 0 и х = а равна нулю, то есть (0) = 0 и (а) = 0.
Согласно этим граничным условиям при х = 0 из (30) следует, что = В. Это означает, что длина волны может быть любой, так как при х = а должно быть = 0. Поэтому
|
|
|
|
, |
(31) |
здесь, n = 1, 2, 3, ...
Следовательно
|
|
|
(32) |
|
|
|
С учётом (32) из (29) имеем |
|
(33) |
Используя условие нормировки (26) для -функции вида (33) можно записать (в условия потенциального ящика интегрирование ведётся от 0 до а)

Определив отсюда значение постоянной |
|
, получаем |
вид волновой функции для частицы в бесконечно глубоком прямоугольном потенциальном ящике |
||
|
|
|
(34) |
Теперь, зная вид волновой функции уже можно проанализировать поведение частицы внутри ящика.
На рис.6(а) на основании формулы (34) приведены графики функции n(x), а на рис.6(б) графики плотности вероятности | n(x)|2 обнаружения частицы внутри ящика для трёх значений квантового числа n.

а) |
б) |
Рис. 6 |
|
Из рис.6(б) следует, что, например, при значении квантового числа n = 2, частица равновероятно может находиться вблизи стенок ящика, а вот вероятность её обнаружения в его центре равна нулю.
Такое поведение частицы говорит о том, что понятие координаты, а значит и траектории движения частицы, в квантовой механике не существует.
Энергия электрона в потенциальной яме
Кинетическую энергию Е можно выразить через длину волны де Бройля (см. 27). Учитывая условие (32), из (27) получаем
|
|
|
(33) |
Выражение (33) позволяет сделать очень важный вывод:
|
Таким образом, согласно уравнения Шредингера, энергия микрочастицы квантуется, а её энергетический спектр — дискретный.
Следует
отметить и ещё один важный момент. Как
видно из (33), энергия микрочастицы никогда
не равна нулю, а принимает минимальное
значение равное
![]() .
.
Эта энергия получила название нулевой. Наличие её у частицы говорит о том, что частицы никогда не прекращают своего движения.
Теперь определим интервал Еn+1, n между двумя соседними уровнями энергии частицы в потенциальном ящике.
Имеем
![]() и
и
![]() ,
тогда
,
тогда
|
(34) |
Если размеры ящика велики, например, а = 1см = 10-2м, то из (34) получаем
![]()
То есть уровни энергии располагаются очень тесно и образуют практически непрерывный спектр.
Если же принять ширину ящика а = 5 = 5 10-10м, то
![]()
Полученные значения говорят о явной дискретности энергетических уровней.
Туннельный эффект
Оправдавшееся предположение Луи де Бройля о существовании у частиц волновых свойств и соотношение неопределённостей Гейзенберга позволили обнаружить у микрочастиц уникального свойства, невозможного в макромире.
Речь идёт о так называемом туннельном эффекте.
Суть туннельного эффекта заключается в возможности прохождения (проникания) частиц сквозь потенциальный барьер. |
|
|
||||||||
|
Запишем уравнения Шредингера для каждой из обозначенных номерами на рис. 6(а) областей: для областей 1 и 3 вне барьера
для области 2 внутри барьера
|
Решение этих уравнений имеет вид:
|
|
|
для области 1 — до барьера |
|
для области 2 — внутри барьера |
|
для области 3 — после барьера |
|
|
|
Здесь |
|
; А1, А3, В1 и В2 — коэффициенты. |
Поскольку уравнение для волновой функции 2(х) внутри барьера не содержит мнимой части, то описываемая им волна не является плоской.
Качественный вид получаемых волновых функций, приведённый на рис.6(б), показывает, что
внутри барьера (область 2) волновая функция не равна нулю, хотя и не представляет собой плоскую волну;
справа от барьера (область 3), если барьер не очень широк, волновая функция имеет вид волны де Бройля с той же частотой и импульсом, что и слева от барьера (область 1), но с меньшей амплитудой.
Из полученных уравнений следует, частица имеет отличную от нуля вероятность прохождения сквозь потенциальный барьер конечной ширины.
Для описания туннельного эффекта вводится понятие коэффициента прозрачности потенциального барьера D. Если по аналогии с оптикой для волн де Бройля подсчитать интенсивность Iпад падающей на барьер волны и интенсивность Iпрох волны, прошедшей сквозь барьер, то прозрачностью (коэффициентом прозрачности) потенциального барьера называется величина
|
(35) |
Эту величину можно рассматривать как вероятность прохождения волн де Бройля сквозь потенциальный барьер.
По аналогии с оптикой можно ввести и коэффициент отражения R, связанный с "прозрачностью" барьера — D = 1 - R. Расчёты, которые выходят за рамки данного курса, показывают, что прозрачность барьера зависит от "высоты" потенциального барьера и его формы.
Для прямоугольного потенциального барьера (рис.6) высотой U0 и шириной L прозрачность барьера выражается формулой
|
|
|
(36) |
где m — масса частицы, а W — её энергия.
В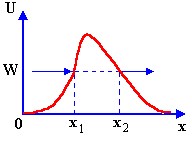 случае, когда потенциальный барьер
имеет сложную форму, прозрачность
барьера подсчитывается по формуле
случае, когда потенциальный барьер
имеет сложную форму, прозрачность
барьера подсчитывается по формуле
|
|
|
(37) |
Здесь х1 и х2 — координаты начала и конца потенциального барьера U(x) для данного значения полной энергии W частицы.
В формулах (36) и (37) D0 — постоянный коэффициент, близкий к единице.
Туннельный эффект получил экспериментальное доказательство после открытия холодной эмиссии электронов из металла. Вырывание электронов из металла происходит при напряжённостях электрического поля в сотни раз меньших, чем тех, что необходимы для преодоления поверхностного скачка потенциала на границе металл-вакуум. Эффект объяснился тем, что под действием внешнего поля ширина потенциального барьера на границе металл-вакуум становилась настолько узкой, что электроны могли проникать сквозь него (туннелировать), даже при собственной энергии меньшей, чем высота этого барьера.
Именно туннельный эффект играет основную роль в явлениях -распада.
Явление автоионизации, при котором электрическое поле вырывает электроны из отдельных атомов при напряжённостях меньших, чем говорит классическая электродинамика, также получило своё объяснение с использованием туннельного эффекта.
Как видно из формул (36) и (37), прозрачность барьера D сильно зависит от массы частицы (экспоненциально уменьшается с увеличением массы), поэтому туннельный эффект проявляется наиболее отчётливо только для микромира.
1. 1. Акустическое поле (см. § 6.3, аускультация, фонокардиография).
2. 2. Электрическое поле (см. § 12.5, электрокардиография).
3. 3. Магнитное поле (см. § 13.5, магнитокардиография).
4. 4. Электромагнитное поле (см. § 22.5, термография).
В популярной литературе часто используется термин «биополе», понимая под этим некоторое специфическое влияние организма на окружающие тела или некоторое специфическое излучение биологических объектов. В связи с этим нужно определенно сказать, что организм является источником физических полей и каких-либо особых «биополей» не создает.
Особый вопрос — как представить результат исследования (регистрации) физического поля организма (органов, тканей) для целей диагностики. Делается это по-разному. Так, например, при аускультации врач выслушивает звуки, т. е. субъективно оценивает их громкость и частоту. При электрокардиографии документально фиксируется временная зависимость разности потенциалов на теле пациента, возникающих при сердечной деятельности. При термографии тепловое излучение отображается на экране тепловизора.
Раздел 7
Физика атомов и молекул. Элементы квантовой биофизики
До конца XIX в. атом считали неделимой частицей. Однако открытие электронов и других элементарных частиц убедило ученых в сложном строении атома.
Решающее значение для понимания структуры атома сыграли знаменитые опыты Резерфорда по рассеянию альфа-частиц. Были созданы условия для развития физики атома, которая изучает строение и состояние атомов и смежные вопросы. Это теория атома, атомная оптическая спектроскопия, рентгеновская спектроскопия, радиоспектроскопия и др.
Отдельные вопросы физики атомов и особенно физики молекул перекликаются с вопросами, рассматриваемыми в химии. Четкие границы раздела в этих областях науки отсутствуют.
Врач должен иметь представление о природе физических и физико-химических процессов, происходящих в организме человека. В конечном счете эти процессы «разыгрываются» на молекулярном уровне. Поэтому здесь рассматриваются вопросы, связанные с энергетическими превращениями молекул в биологических системах (хемилюминесценция, фотобиологические явления и др.). Эти темы объединяют термином «квантовая биофизика», видимо, по созвучию с квантовой механикой.
Глава 23
Волновые свойства частиц. Элементы квантовой механики
Квантовой механикой называют теорию, устанавливающую способ описания и законы движения микрочастиц (элементарных частиц, ядер, атомов, молекул и их систем, в частности кристаллов, и т. д.)- Необычность квантово-механических представлений по сравнению с классической физикой инициировала пересмотр основных физических моделей и представлений, которые казались очевидными и незыблемыми. Прежде всего, это коснулось понятия самих частиц и принципов их движения.
В этой главе дается понятие не только о квантовой механике, но и о тех идеях и опытах, которые привели к этой теории. Здесь также рассматривается электронная микроскопия как метод, основанный на волновых свойствах электронов.
§ 23.1. Гипотеза де Бройля.
Опыты по дифракции электронов и других частиц
Важным этапом в создании квантовой механики явилось установление волновых свойств микрочастиц. Идея о волновых свойствах частиц была первоначально высказана как гипотеза французским физиком Луи де Бройлем (1924)1. Эта гипотеза появилась благодаря следующим предпосылкам.
В физике в течение многих лет господствовала теория, согласно которой свет есть электромагнитная волна. Однако после работ Планка (тепловое излучение), Эйнштейна (фотоэффект) и др. стало очевидным, что свет обладает корпускулярными свойствами.
Чтобы
объяснить некоторые физические явления,
необходимо рассматривать свет как поток
частиц — фотонов. Корпускулярные
свойства света не отвергают, а дополняют
его волновые свойства. Итак, фотон
—
элементарная
частица, движущаяся со скоростью света,
обладающая волновыми свойствами и
имеющая энергию
![]() ,
где
,
где
![]() —
частота
световой волны.
—
частота
световой волны.
Логично считать, что и другие частицы — электроны, нейтроны также обладают волновыми свойствами.
Выражение
для импульса фотона
![]() получается
из известной формулы Эйнштейна
получается
из известной формулы Эйнштейна
![]() и
соотношений и
и
соотношений и
![]() J
J
![]()
![]() (23.1)
(23.1)
где
с
—
скорость света в вакууме,
![]() —
длина световой волны. Эта формула была
использована де Бройлем и для других
микрочастиц массой т,
движущихся
со скоростью v:
—
длина световой волны. Эта формула была
использована де Бройлем и для других
микрочастиц массой т,
движущихся
со скоростью v:
![]() ,
откуда
,
откуда
![]() (23.2)
(23.2)
По
де Бройлю, движение частицы, например
электрона, описывается волновым
процессом с характеристической длиной
волны
![]() ,
в соответствии с формулой (23.2). Эти волны
называют волнами
де Бройля.
,
в соответствии с формулой (23.2). Эти волны
называют волнами
де Бройля.
Гипотеза де Бройля была столь необычной, что многие крупные физики-современники не придали ей какого-либо значения. Несколькими годами позже эта гипотеза получила экспериментальное подтверждение: была обнаружена дифракция электронов.
Найдем зависимость длины волны электрона от ускоряющего напряжения U электрического поля, в котором он движется. Изменение кинетической энергии электрона равно работе сил поля:
![]()
Выразим отсюда скорость v и, подставив ее в (23.2), получим
![]() (23.3)
(23.3)
Для
получения пучка электронов с достаточной
энергией, который можно зафиксировать,
например, на экране осциллографа,
необходимо ускоряющее напряжение
порядка 1 кВ. В этом случае из (23.3) находим
![]() =
0,4 • 10~10
м, что соответствует длине волны
рентгеновского излучения.
=
0,4 • 10~10
м, что соответствует длине волны
рентгеновского излучения.
В гл. 19 было отмечено, что дифракция рентгеновских лучей наблюдается на кристаллических телах; следовательно, для дифракции электронов необходимо также использовать кристаллы.
К. Дэвиссон и Л. Джермер впервые наблюдали дифракцию электронов на монокристалле никеля, Дж. П. Томсон и независимо от него П. С. Тартаковский — на металлической фольге (поликристаллическое тело). На рис. 23.1 изображена электронограм-ма — дифракционная картина, полученная от взаимодействия электронов с поликристаллической фольгой. Сравнивая этот рисунок с рис. 19.21, можно заметить сходство дифракции электронов и рентгеновских лучей.
Способностью дифрагировать обладают и другие частицы, как заряженные (протоны, ионы и др.), так и нейтральные (нейтроны, атомы, молекулы).
Аналогично рентгеноструктурному анализу можно применять дифракцию частиц для оценки степени упорядоченности расположения атомов и молекул вещества, а также для измерения параметров кристаллических решеток. В настоящее время широкое распространение имеют методы электронографии (дифракция электронов) и нейтронографии (дифракция нейтронов).
Может возникнуть вопрос: что происходит с отдельными частицами, как образуются максимумы и минимумы при дифракции отдельных частиц?
Опыты по дифракции пучков электронов очень малой интенсивности, т. е. отдельных частиц, показали, что при этом электрон
 не
«размазывается» по разным направлениям,
а ведет себя как целая частица. Однако
вероятность отклонения электрона
по отдельным направлениям в результате
взаимодействия с объектом дифракции
различна. Наиболее вероятно попадание
электронов в те места, которые по
расчету соответствуют максимумам
дифракции, менее вероятно их попадание
в места минимумов. Таким образом, волновые
свойства присущи не только коллективу
электронов, но и каждому электрону в
отдельности.
не
«размазывается» по разным направлениям,
а ведет себя как целая частица. Однако
вероятность отклонения электрона
по отдельным направлениям в результате
взаимодействия с объектом дифракции
различна. Наиболее вероятно попадание
электронов в те места, которые по
расчету соответствуют максимумам
дифракции, менее вероятно их попадание
в места минимумов. Таким образом, волновые
свойства присущи не только коллективу
электронов, но и каждому электрону в
отдельности.
![]()
1 Гипотеза де Бройля была сформулирована до опытов, подтверждающих волновые свойства частиц. Де Бройль об этом позднее, в 1936 г. писал так: «...не можем ли мы предположить, что и электрон так же двойственен, как и свет? На первый взгляд такая идея казалась очень дерзкой. Ведь мы всегда представляли себе электрон в виде электрически заряженной материальной точки, которая подчиняется законам классической динамики. Электрон никогда не проявлял волновых свойств, таких, скажем, какие проявляет свет в явлениях интерференции и дифракции. Попытка приписать волновые свойства электрону, когда этому нет никаких экспериментальных доказательств, могла выглядеть как ненаучная фантазия».

 Рис.
1. Схема
опыта Дэвидсона
и Джермера:
1
— нить накала, 2
— диафрагмы,
3
— кристалл никеля, 4
— ионизационная камера, 5
— гальванометр.
Рис.
1. Схема
опыта Дэвидсона
и Джермера:
1
— нить накала, 2
— диафрагмы,
3
— кристалл никеля, 4
— ионизационная камера, 5
— гальванометр. Рис.
2
Рис.
2 Рис.
3.
Снимки дифракционных колец, полученные
Джорджем
П.Томсоном
при пропускании электронов через
тонкую золотую фольгу
Рис.
3.
Снимки дифракционных колец, полученные
Джорджем
П.Томсоном
при пропускании электронов через
тонкую золотую фольгу
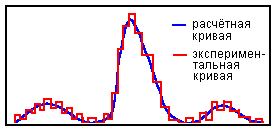 Рис.
5
Рис.
5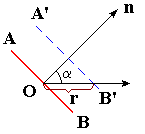
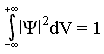
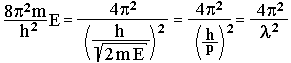
 Рис.
6
Рис.
6