5. Электромагниты

Обоб­щим вы­во­ды из про­де­лан­ных экс­пе­ри­мен­тов. На дви­жу­щий­ся в маг­нит­ном поле заряд (q) со сто­ро­ны маг­нит­но­го поля дей­ству­ет сила (F), на­прав­ле­ние ко­то­рой за­ви­сит от вза­им­но­го на­прав­ле­ния век­то­ра ско­ро­сти дви­же­ния ( ) за­ря­да и век­то­ра маг­нит­ной ин­дук­ции поля (В). Ве­ли­чи­на силы про­пор­ци­о­наль­на ско­ро­сти дви­же­ния за­ря­да и мо­ду­лю маг­нит­ной ин­дук­ции. На­прав­ле­ние силы опре­де­ля­ет­ся по пра­ви­лу «Левой руки» (рис. 4).

 (1.7)

Таким об­ра­зом, по­лу­чен­ное ранее вы­ра­же­ние для силы, опи­сы­ва­ет вза­и­мо­дей­ствие маг­нит­но­го поля с дви­жу­щим­ся в этом поле элек­три­че­ским за­ря­дом. От­кры­тие силы дей­ствия маг­нит­но­го поля на дви­жу­щий­ся в нём заряд стало воз­мож­ным толь­ко бла­го­да­ря улуч­ше­нию пред­став­ле­ний о стро­е­нии ве­ще­ства, элек­три­че­ском токе в ме­тал­лах, дви­же­нии за­ря­жен­ных ча­стиц. И огром­ную роль во всех этих за­да­чах сыг­рал Ло­ренц, по­это­му от­кры­тая сила и по­лу­чи­ла на­зва­ние – сила Ло­рен­ца.

6. Выводы

Сде­ла­ем ещё несколь­ко за­ме­ча­ний.

1. Век­тор силы Ло­рен­ца пер­пен­ди­ку­ля­рен век­то­ру ско­ро­сти

  (1.8)

 (1.9)

   (1.10)

2. Если сила пер­пен­ди­ку­ляр­на век­то­ру ско­ро­сти, то такая сила на­зы­ва­ет­ся цен­тро­стре­ми­тель­ной. И тогда под её дей­стви­ем – тело дви­жет­ся по окруж­но­сти. Сле­до­ва­тель­но, сила Ло­рен­ца – цен­тро­стре­ми­тель­ная сила:

  (1.11)

3. Из-за того, что под дей­стви­ем силы Ло­рен­ца заряд дви­жет­ся по дуге окруж­но­сти, сле­до­ва­тель­но, он об­ла­да­ет цен­тро­стре­ми­тель­ным уско­ре­ни­ем. Цен­тро­стре­ми­тель­ное уско­ре­ние может быть рас­счи­та­но как квад­рат ско­ро­сти дви­же­ния, де­лён­ный на ра­ди­ус окруж­но­сти, ко­то­рый опи­сы­ва­ет тело:

  (1.12)

4. Так, со­глас­но вто­ро­му за­ко­ну Нью­то­на сила может быть опре­де­ле­на как про­из­ве­де­ние массы тела на при­об­ре­та­е­мое им уско­ре­ние:

  (1.13)

После под­ста­нов­ки урав­не­ния 1.12 в 1.13 по­лу­чим:

    (1.14)

После со­кра­ще­ния ско­ро­сти по­лу­чим сле­ду­ю­щие со­от­но­ше­ния:

 (1.15)

  (1.16)

   (1.17.)

Действие магнитного поля на движущийся заряд. Сила Лоренца

Электрический ток – это совокупность упорядоченно движущихся заряженных частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника.

Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.

Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:

Сила Ампера равна   , сила тока равна   (см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:

где   - угол между векторами скорости и магнитной индукции.

Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).

Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.

 

Закон Ампера

Поместим в магнитное поле проводник длинной l, по которому течет ток I. На проводник действует сила, прямо пропорциональная силе тока, текущего по проводнику, индукции магнитного поля, длине проводника, и зависящая от ориентации проводника в магнитном поле. |F|=IBlsina, где a - угол между направлением тока в проводнике и направлением вектора магнитной индукции B, Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, что магнитные силовые линии входят в ладонь, четыре вытянутых пальца направить по току, то отогнутый большой палец укажет направление силы. Очевидно, что сила Ампера равна нулю, если проводник расположен вдоль силовых линий поля и максимальна, если проводник перпендикулярен силовым линиям. Движение заряженных частиц в магнитном поле. На проводник с током в магнитном поле действует сила Ампера F_А IBlsina.Ток, в свою очередь, это направленное движение заряженных частиц. Сила тока равна I=qnvS, где q – заряд частицы, n-концентрация движущихся заряженных частиц, v-средняя скорость их направленного движения, S-площадь поперечного сечения проводника. Подставив I в выражение для F_А, получим F_А= qnvSBlsina, где nsl=N – общее число частиц, создающих ток. Тогда сила, действующая на отдельный движущийся заряд – сила Лоренца, равна Fл=qvBsina. где a - угол между векторами скорости и магнитной индукции. Направление силы Лоренца определяется для положительно заряженной частицы по правилу левой руки.

Закон Ампера

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.

Экспериментальное изучение магнитного взаимодействия показывает, что модуль силы Ампера пропорционален длине проводника с током, силе тока и зависит от ориентации проводника в магнитном поле.

Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.

Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника:

Направление силы ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 большой палец покажет направление силы, действующей на отрезок проводника.

Магнитное взаимодействие проводников с током используется в Международной системе для определения единицы сила тока –ампера.

Ампер –сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную Н на каждый метр длины.

Действие магнитного поля на движущиеся заряды. Сила Лоренца

На заряды, движущиеся в магнитном поле, действует сила, которую называют силой Лоренца. Эта сила определяется величиной заряда q, скоростью его движения  и магнитной индукцией  в той точке, где находится заряд в данный момент от взаимной ориентации векторов  и .Направление векторов  и  определяют направление силы Лоренца. Итак, сила Лоренца:

. (4.4.1)

Модуль силы Лоренца:

, (4.4.2)

где a - угол между  и  .

Если заряженная частица покоится ( = 0), то магнитное поле на нее не действует. Магнитное поле действует только на движущиеся в нем заряды. Направлена сила Лоренца перпендикулярно к плоскости, в которой лежат вектора и (см. рис.20.11). Если заряд отрицательный, то сила  имеет противоположное (указанному на рисунке) направление. Направление силы Лоренца может быть определено и с помощью правила левой руки. Так как сила Лоренца всегда направлена перпендикулярно к скорости заряженной частицы, она не совершает работы над частицей. Величина скорости и, следовательно, кинетической энергии частицы не

i i i

+Q 

 i i

i i i

Рис.20.11

изменяются, изменяется лишь направление скорости, т.е. заряженная частица, движущаяся в однородном магнитном поле, приобретает постоянное по величине нормальное ускорение. Итак, если частица движется в магнитном поле со скоростью  вдоль линий магнитной индукции, то сила Лоренца равна нулю (угол a между векторами  и  равен 0 или p) и скорость частицы остается постоянной. Если же скорость  перпендикулярна  , то сила Лоренца постоянна по модулю и нормальна к траектории частицы и создает центростремительное ускорение (согласно второму закону Ньютона). Радиус траектории может быть определен из соотношения:

F_л = F_цс или 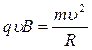 , (4.4.3)

откуда:

. (4.4.4)

Радиус частицы зависит от скорости  , магнитной индукции и удельного заряда  . Определим период вращения частицы (время полного оборота), разделив длину окружности на скорость.

, (4.4.5)

т.е. период вращения не зависит от скорости при  «с, а зависит лишь от индукции магнитного поля  и величины, обратной удельному заряду  . Если скорость  заряженной частицы ориентирована относительно вектора  , произвольным образом, то следует разложить вектор начальной скорости на составляющие: параллельную магнитному полю,  ₁₁и перпендикулярную к нему  ^ (рис 20.12 ).

Рис.20.12

Составляющая  ₁₁ в процессе движения остается постоянной, т.к. сила Лоренца не имеет составляющей, направленной вдоль силовой линии

.

В плоскости перпендикулярной полю, частица равномерно движется по окружности со скоростью  ^ =  sina. Радиус окружности:

.

Сложение обоих движений (равномерного перемещения вдоль направления магнитного поля и равномерного вращения в перпендикулярной плоскости) приводит к движению частицы по винтовой линии. Шаг винтовой линии:

h=  ₁₁ T =  Tcosa (4.4.6)

или h = 2p m cosa / (Bq). (4.4.7)

Направление, в котором закручивается спираль, зависит от знака заряда частицы. Если имеются одновременно электрическое и магнитное поля, то лоренцева сила, действующая на заряженную частицу, равна:

. (4.4.8)