
Решение типового варианта.
Часть 1 Линейная алгебра. Аналитическая геометрия
Задача 1.
Вычислить
определитель
 .
.
Решение.
Способ 1.
Вычислим определитель методом понижения порядка.
Выносим
за знак определителя из четвертого
столбца общий множитель
 :
:
 ,
,
,
а затем будем последовательно умножать
третью строку на
 и складывать соответственно с первой
и со второй строками. Имеем
и складывать соответственно с первой
и со второй строками. Имеем
 .
.
Далее полученный определитель раскладываем по элементам третьего столбца
 .
.
Получим
определитель третьего порядка, который
можно вычислить по правилу Саррюса или
подобным приемом свести к вычислению
одного определителя второго порядка.
Для этого последовательно умножим
элементы первого столбца на
 и прибавим соответственно к элементам
второго и третьего столбцов. Получаем
и прибавим соответственно к элементам
второго и третьего столбцов. Получаем
 .
.
Полученный определитель раскладываем по элементам третьей строки, имеем:
 .
.
Способ 2.
Вычислим определитель методом приведения его к треугольному виду.
Выполним
следующие операции. Выносим за знак
определителя из четвертого столбца
общий множитель
 ,
а затем переставим местами первую и
четвертую строки – определитель меняет
свой знак на противоположный:
,
а затем переставим местами первую и
четвертую строки – определитель меняет
свой знак на противоположный:
 .
.
Далее,
первую строку определителя сложим со
второй, эту же строку, умноженную на
 с третьей, на
с третьей, на
 с четвертой строкой. В итоге получим
определитель, который равен исходному:
с четвертой строкой. В итоге получим
определитель, который равен исходному:
 .
.
Вторую
строку определителя умножим на
 и сложим с третьей:
и сложим с третьей:
 .
.
Из четвертой строки вычтем третью:
 .
.
Определитель треугольного вида равен произведению элементов его главной диагонали. Имеем
 .
.
Задача 2.
Даны
матрицы
 и
и
 .
Найдите матрицу
.
Найдите матрицу
 ,
если
,
если
 .
.
Решение.

 .
.
Задача 3.
Какое
из произведений существует
 или
или
 ?
Почему? Найдите это произведение, если
?
Почему? Найдите это произведение, если
 .
.
Решение.
Произведение
матриц определено только в том случае,
когда число столбцов первой матрицы
равно числу строк второй матрицы.
Произведение матриц содержит столько
строк, сколько имеет первая матрица, и
столько столбцов, сколько имеет вторая
матрица. Для заданных матриц определено
только произведение
 .
.
 .
.
Задача 4.
Решите систему уравнений тремя способами:
-
по формулам Крамера;
-
с помощью обратной матрицы (матричным методом);
-
методом Жордана - Гаусса.
Выполните проверку.
Решение.
1)
Если определитель
 системы линейных алгебраических
уравнений отличен от нуля, то система
имеет единственное решение, которое
может быть найдено по формулам Крамера
системы линейных алгебраических
уравнений отличен от нуля, то система
имеет единственное решение, которое
может быть найдено по формулам Крамера
 ,
,
где
 определитель системы,
определитель системы,
 вспомогательные
определители, которые получаются из
определителя
вспомогательные
определители, которые получаются из
определителя
 заменой столбца из коэффициентов
соответственно при
заменой столбца из коэффициентов
соответственно при
 столбцом свободных членов.
столбцом свободных членов.
Определитель системы равен
 .
.
Вычислим вспомогательные определители:
 ;
;
 ;
;
 .
.
По формулам Крамера найдем:

2) Систему линейных алгебраических уравнений можно записать в виде матричного уравнения:
 ,
,
где
 матрица системы;
матрица системы;
 столбец неизвестных;
столбец неизвестных;
 столбец свободных членов.
столбец свободных членов.
Если
матрица
 невырожденная, то решение системы
определяется по формуле:
невырожденная, то решение системы
определяется по формуле:
 ,
,
где
 обратная матрица.
обратная матрица.
Для данной системы

столбец
неизвестных
 ,
столбец свободных членов
,
столбец свободных членов
 .
.
Найдем
обратную матрицу
 по формуле
по формуле
 ,
,
где
 определитель матрицы
определитель матрицы
 ,
,
 союзная
матрица, которая получается из матрицы
союзная
матрица, которая получается из матрицы
 заменой всех ее элементов соответствующими
им алгебраическими дополнениями.
заменой всех ее элементов соответствующими
им алгебраическими дополнениями.
Определитель матрицы
 .
.
Вычислим
алгебраические дополнения для элементов
матрицы
 по формуле
по формуле
 ,
,
где
 минор элемента
минор элемента
 .
.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,  .
.
Составим союзную матрицу
 .
.
Обратная матрица будет равна
 ,
,
 .
.
Проверим
правильность нахождения обратной
матрицы, используя соотношение
 .
.

 .
.
Теперь можно получить решение системы в матричном виде:
 .
.
 .
.
3) Метод Жордана – Гаусса (метод полного исключения неизвестных).
Пусть
задана СЛАУ
 .
Запишем ее расширенную матрицу
.
Запишем ее расширенную матрицу
 .
Каждому элементарному преобразованию
строк расширенной матрицы соответствует
аналогичное преобразование уравнений
в исходной СЛАУ.
.
Каждому элементарному преобразованию
строк расширенной матрицы соответствует
аналогичное преобразование уравнений
в исходной СЛАУ.
Элементарные преобразования в расширенной матрице:
-
перемена местами строк;
-
перемена местами столбцов с запоминанием, какому неизвестному соответствует каждый столбец;
-
умножение (деление) строки на ненулевую постоянную;
-
прибавление к любой строке линейную комбинацию других строк;
-
вычеркивание одной из двух пропорциональных (равных) строк;
-
вычеркивание нулевой строки.
Эти преобразования не меняют множество решений системы.
Если
элементарными преобразованиями строк
матрица
 переведена в матрицу
переведена в матрицу
 ,
то столбец
,
то столбец
 есть решением системы линейных уравнений
есть решением системы линейных уравнений
 .
.
Составим
расширенную матрицу
 и проведем необходимые элементарные
преобразования:
и проведем необходимые элементарные
преобразования:



 .
.
 .
.
Проверка.
Подставив полученное решение в систему, убедимся в правильности полученного решения:

Задача 5.
Найдите общее решение, построив фундаментальную систему для однородной системы алгебраических уравнений.

Решение.
Составим
матрицу
 однородной СЛАУ и проведем необходимые
элементарные преобразования строк
однородной СЛАУ и проведем необходимые
элементарные преобразования строк

 .
.
 ,
где
,
где
 число
неизвестных. Система имеет нетривиальные
решения. Базисный минор
число
неизвестных. Система имеет нетривиальные
решения. Базисный минор
 .
Число свободных переменных
.
Число свободных переменных
 .
Пусть
.
Пусть
 базисные переменные,
базисные переменные,
 свободные переменные.
свободные переменные.
Исходная система равносильна системе из двух уравнений

Общее решение:
 .
.
Полагая
 и
и
 ,
из общего решения получим фундаментальную
систему решений (Ф.С.Р.):
,
из общего решения получим фундаментальную
систему решений (Ф.С.Р.):
 .
.
Общее решение системы имеет вид
 .
.
Задача 6.
Исследовать на совместность и в случае совместности найдите общее решение методом Жордана – Гаусса и одно частное решение системы. Выполните проверку.

Решение.
Используем
метод Жордана – Гаусса (метод полного
исключения). Составим расширенную
матрицу
 неоднородной СЛАУ и проведем необходимые
элементарные преобразования строк:
неоднородной СЛАУ и проведем необходимые
элементарные преобразования строк:

 .
.
 ,
где
,
где
 число
неизвестных. Система совместна, имеет
бесчисленное множество решений. Базисный
минор
число
неизвестных. Система совместна, имеет
бесчисленное множество решений. Базисный
минор
 .
Число свободных переменных
.
Число свободных переменных
 .
Пусть
.
Пусть
 базисные переменные,
базисные переменные,
 свободные переменные.
свободные переменные.
Исходная система равносильна системе из двух уравнений

Общее решение неоднородной СЛАУ представим так:
 .
.
Полагая,
например,
 ,
найдем частное решение:
,
найдем частное решение:
 .
.
Непосредственной подстановкой в систему частного решения убедимся в его правильности:

Задача 7.
Найдите
координаты, модуль и направляющие
косинусы вектора
 ,
его орт, если
,
его орт, если
 .
.
Решение.
Найдем
координаты вектора
 :
:
 ;
;
 .
.
Длина
вектора
 определяется так:
определяется так:
 или
или
 ;
;
 .
.
Направляющие
косинусы вектора
 определяется по следующим формулам:
определяется по следующим формулам:
 .
.
Следовательно,
 .
.
Вектор
 является ортом (единичным вектором)
вектора
является ортом (единичным вектором)
вектора
 .
.
 .
.
Задача 8.
Вычислите
скалярное и векторное произведения
векторов
 ,
если
,
если
 .
Являются ли векторы
.
Являются ли векторы
 и
и
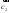 коллинеарными? Являются ли векторы
коллинеарными? Являются ли векторы
 и
и
 ортогональными?
ортогональными?
Решение.
 .
.
 .
.
Скалярное произведение:
 ;
;
 .
.
Векторное произведение:
 ;
;
 .
.
Условие
коллинеарности векторов
 и
и
 :
:
 векторы
векторы
 не коллинеарны.
не коллинеарны.
Условие
ортогональности векторов
 и
и
 :
:
 векторы
векторы
 не ортогональны.
не ортогональны.
Задача 9.
Заданы
вершины треугольника
 .
Вычислите его площадь и косинус
внутреннего угла
.
Вычислите его площадь и косинус
внутреннего угла
 .
.
Решение.
Внутренний
угол
 в треугольнике
в треугольнике
 это угол между векторами
это угол между векторами
 и
и
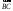 .
Здесь
.
Здесь
 ,
,
 .
.
 ;
;
 .
.
Площадь треугольника вычисляется по формуле
 .
.
Вычислим
векторное произведение векторов
 и
и
 :
:
 .
.
Тогда площадь треугольника
 .
.
Задача 10.
Выясните,
образуют ли векторы
 базис. Если образуют, то разложите вектор
базис. Если образуют, то разложите вектор
 по этому базису.
по этому базису.
 .
.
Решение.
Поскольку
определитель
 ,
векторы
,
векторы
 не компланарны, следовательно, линейно
независимые.
не компланарны, следовательно, линейно
независимые.
Найдем
координаты вектора
 в базисе
в базисе
 .
Запишем
.
Запишем
 ,
или
,
или
 .
.
Это векторное равенство равносильно системе линейных уравнений:

Методом Жордана – Гаусса решим систему:


 .
.
Таким
образом,
 .
.
Задача 11.
Вычислите
площадь
 параллелограмма, построенного на
векторах
параллелограмма, построенного на
векторах
 и
и
 ,
если
,
если
 .
.
Решение.
Площадь
параллелограмма, построенного на
векторах
 и
и
 ,
равна
,
равна
 .
.
Согласно свойствам векторное произведение векторных многочленов производится по тем же правилам, что и умножение алгебраических многочленов. Тогда, используя антикоммутативность векторного произведения и тот факт, что векторное произведение вектора на самого себя равно нуль – вектору, получим

 .
.
Задача 12.
Вычислить
 ,
если
,
если
 .
.
Решение.


 .
.
Задача 13.
Найти
вектор
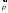 ,
ортогональный векторам
,
ортогональный векторам
 и
и
 и удовлетворяет условию
и удовлетворяет условию
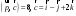 .
.
Решение.
Вектор
 коллинеарен векторному произведению
коллинеарен векторному произведению
 ,
следовательно,
,
следовательно,
 .
Поскольку
.
Поскольку
 ,
,
то
 .
.
Так
как
 ,
то
,
то
 ,
,
 ,
,
 .
.
Теперь можно определить координаты вектора
 .
.
Задача 14.
Принадлежат
ли точки
 и
и
 одной плоскости?
одной плоскости?
Решение.
Точки
 и
и
 лежат в одной плоскости, если векторы
лежат в одной плоскости, если векторы
 и
и
 компланарны. Найдем координаты этих
векторов:
компланарны. Найдем координаты этих
векторов:

 ;
;

 ;
;
 ,
,
 .
.
Проверим их компланарность
 ,
,
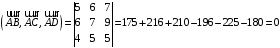 .
.
Точки
 и
и
 лежат в одной плоскости.
лежат в одной плоскости.
Задача 15.
Заданы
прямая
 и точка
и точка
 .
Запишите:
.
Запишите:
1)
уравнение прямой, проходящей через
точку
 параллельно прямой
параллельно прямой
 ;
;
2)
уравнение прямой, проходящей через
точку
 перпендикулярно прямой
перпендикулярно прямой
 .
.
Решение.
Преобразуем общее уравнение данной прямой в уравнение с угловым коэффициентом
 .
.
1)
Так как искомая прямая параллельна
данной, то ее угловой коэффициент
 равен угловому коэффициенту данной
прямой, следовательно,
равен угловому коэффициенту данной
прямой, следовательно,
 .
Тогда по точке
.
Тогда по точке
 и угловому коэффициенту
и угловому коэффициенту
 составляем уравнение прямой
составляем уравнение прямой
 ,
,
 ,
,
 .
.
2)
С учетом условия перпендикулярности
прямых угловой коэффициент искомой
прямой
 .
Тогда по точке
.
Тогда по точке
 и угловому коэффициенту
и угловому коэффициенту
 составляем уравнение прямой
составляем уравнение прямой
 ,
,
 ,
,
 .
.
Задача 16.
Напишите
уравнение прямой, которая проходит
через точку
 и через точку пересечения прямых
и через точку пересечения прямых
 .
.
Решение.
Для
нахождения координат точки
 пересечения прямых
пересечения прямых
 и
и
 составляем систему уравнений
составляем систему уравнений

Решая
ее, получаем
 .
.
Теперь
по двум известным точкам
 и
и
 составляем уравнение искомой прямой:
составляем уравнение искомой прямой:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Задача 17.
Даны
вершины треугольника
 .
Найти:
.
Найти:
-
уравнение стороны
 и длину
и длину
 ;
; -
уравнение высоты, опущенной из вершины
 на сторону
на сторону
 ;
; -
уравнение медианы, проведенной из вершины
 .
.
Решение.
-
Воспользовавшись уравнением прямой, проходящей через две точки, получим уравнение стороны
 :
:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Расстояние
между точками
 и
и
 определяется по формуле:
определяется по формуле:
 ,
,
 .
.
-
С учетом перпендикулярности прямых
 и
и
 угловой коэффициент высоты
угловой коэффициент высоты
 .
Преобразуем общее уравнение прямой
.
Преобразуем общее уравнение прямой
 в уравнение с угловым коэффициентом
в уравнение с угловым коэффициентом
 .
.
По
точке
 и угловому коэффициенту
и угловому коэффициенту
 составляем уравнение высоты
составляем уравнение высоты
 :
:
 ,
,
 ,
,
 .
.
-
По известным формулам находим координаты середины
 отрезка
отрезка
 :
:
 ;
;
 .
.
Теперь
по двум известным точкам
 и
и
 составляем уравнение медианы
составляем уравнение медианы
 :
:
 ,
,
 ,
,
 ,
,
 .
.
