Вопрос 3. Необходимое и достаточное условие существования определенного интеграла

Т.3.1. (необходимое условие существования определенного интеграла)

Если функция y = f(x) интегрируема на отрезке [a;b], то она ограничена на этом отрезке.

Замечание

Обратная теорема неверна, т.е. из ограниченности функции y = f(x) еще не следует ее интегрируемость.

Пример. Рассмотрим функцию Дирихле, которая имеет широкое применение в технических приложениях:

Для функции Дирихле:

1. Если c_i - рациональное число, то

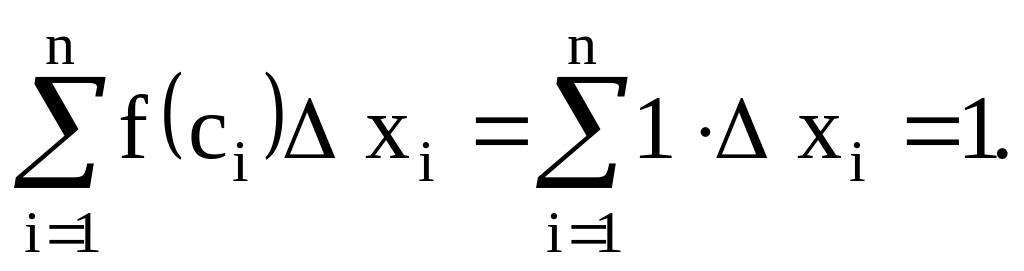
2. Если c_i - иррациональное число, то

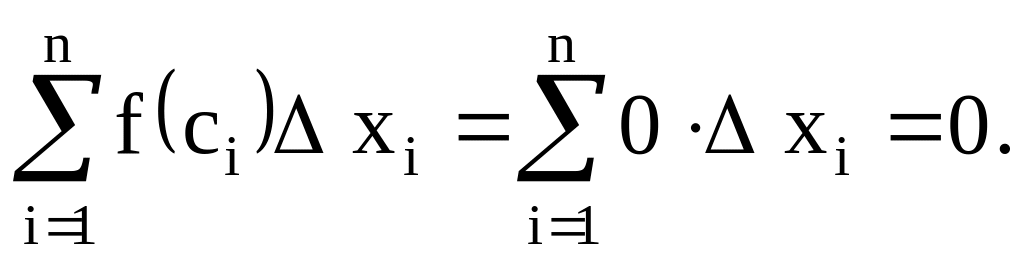
Очевидно, что для функции Дирихле предел интегральной суммы (3) не существует, следовательно, не существует и определенный интеграл от данной функции. При этом функция Дирихле ограничена.

Классы интегрируемых функций

T.3.2. (достаточное условие существования определенного интеграла)

Если функция y = f(x) непрерывна на отрезке [a;b], то она интегрируема на нем.

Условие непрерывности функции является достаточным условием интегрируемости функции. Но это не означает, что определенный интеграл существует только для непрерывных функций. Класс интегрируемых функций гораздо шире.

Т.3.3.Если функция y = f(x) ограничена на отрезке [a;b] и имеет на нем конечное число точек разрыва, то она интегрируема на этом отрезке.

Т.3.4. Всякая функция y = f(x), ограниченная и монотонная на отрезке [a;b], интегрируема на нем.

Вопрос 4. Геометрический, физический смысл определенного интеграла

Геометрический смысл определенного интеграла

(вытекает из задачи о площади криволинейной трапеции)

Если функция y = f(x) непрерывна и неотрицательна на отрезке [a;b], то интеграл геометрически представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции y = f(x), снизу – осью Ох, с боков – прямыми x = a и x = b:

.

Физический смысл определенного интеграла

(вытекает из задачи о пройденном пути)

Пусть функция ʋ = ʋ(t) представляет собой зависимость скорости движения ʋ материальной точки от времени t, причем ʋ(t) непрерывна на промежутке [;]. Тогда интеграл представляет собой путь S, пройденный точкой за промежуток времени от  до :

.

На лекции мы рассмотрели некоторые задачи, приводящие к понятию определенного интеграла; ввели понятие определенного интеграла как предела интегральных сумм и определили классы интегрируемых функций. На следующей лекции мы покажем, как вычисляется определенный интеграл, и рассмотрим основную формулу интегрального исчисления.

6