Передаточная функция дискретной цепи.
Замена сигналов в разностном уравнении (2.1) на Z - изображения этих сигналов
, 
приводит к алгебраизации разностного уравнения
.
Алгебраизация осуществляется применением теорем линейности и запаздывания.
Переход в область Z - изображений позволяет ввести понятие передаточной функции дискретной цепи H(Z), которая определяется как отношение Z - изображения сигнала на выходе цепи к Z - изображению сигнала на входе цепи. Поэтому, учитывая алгебраическую форму разностного уравнения общего вида, можно записать общий вид передаточной функции дискретной цепи
.
(2.3)
Отсюда, в частности, для нерекурсивной цепи
.
(2.4)
Если
нерекурсивная цепь состоит всего из
одного элемента запаздывания, то 
,
что находит своё отражение в обозначении элементов памяти на схемах дискретных цепей.
Передаточная функция конкретной цепи формируется по передаточным функциям её элементов согласно общих правил линейных цепей. В частности, для цепи содержащей ОС применяется известная формула
,
(2.5)
где 
-
передаточная функция цепи прямого
прохождения сигнала,
-
предаточная функция цепи ОС.
Импульсная характеристика дискретной цепи
Обычно нас интересуют линейные дискретные цепи. Особенностью этих дискретных цепей является то, что на выходе не образуется новых частотных составляющих сигнала. Если дискретная цепь является фильтром, то соотношение частотных компонент спектра входного сигнала на выходе изменяется. Это удается сделать при помощи дискретной свертки сигнала. Формула дискретной свертки входной последовательности отсчетов с импульсной характеристикой дискретной цепи (фильтра) записывается следующим образом:
(1)
где h(k) — импульсная характеристика дискретной цепи. Импульсную характеристику можно определить как отклик дискретной цепи на воздействие единичного импульса (δ-функция). Формулу свертки (1) можно записать в сокращенном виде, используя символ операции свертки '*':
y(k) = x(k)*h(k) (2).
Связь переходной характеристики h(t) с операторной передаточной функцией Н(р).
По определению, операторная передаточная функция
(2)
где 
-
изображение воздействия цепи (
или
);
-
изображение реакции цепи (
или
).
Из (2) следует, что
.
(3)
Если
в качестве воздействия на цепь подать
единичную ступенчатую функцию 
,
то ее изображение будет
.
При этом реакцией цепи будет переходная
характеристика цепи
.
Изображение реакции цепи
можно
найти, воспользовавшись выражением
(3):
(4)
Формула
(4) выражает связь между переходной
характеристикой цепи 
и
операторной передаточной функцией
а
также позволяет определять переходную
характеристику цепи
по
известной операторной передаточной
функции
.
Быстрым преобразованием Фурье (БПФ) называют набор алгоритмов, реализация которых приводит к существенному уменьшению вычислительной сложности ДПФ. Основная идея БПФ состоит в том, чтобы разбить исходный N-отсчетный сигнал x(n) на два более коротких сигнала, ДПФ которых могут быть скомбинированы таким образом, чтобы получить ДПФ исходного N-отсчетного сигнала.
Так, если исходный N-отсчетный сигнал разбить на два N/2-отсчетных сигнала, то для вычисления ДПФ каждого из них потребуется около (N/2)2 комплексных умножений. Тогда для вычисления искомого N-отсчетного ДПФ потребуется порядка 2(N/2)2=N2/2 комплексных умножений , т.е. вдвое меньше по сравнению с прямым вычислением. Операцию разбиения можно повторить, вычисляя вместо (N/2)-отсчетного ДПФ два (N/4)-отсчетных ДПФ и сокращая тем сасым объем вычислений еще в два раза. Выигрыш в два раза является приблизительным, поскольку не учитывается, каким образом из ДПФ меньшего размера образуется искомое N-отсчетное ДПФ.
Определение 1 .
Дана конечная последовательность x0 , x1 , x2 ,...,xN-1 (в общем случае комплексных). Дискретное преобразование Фурье (ДПФ) заключается в поиске другой последовательности X0 , X1 , X2 ,...,XN-1 элементы которой вычисляются по формуле:
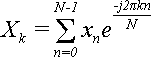(1).
Определение 2 .
Дана конечная последовательность X0 , X1 , X2 ,...,XN-1 (в общем случае комплексных). Обратное дискретное преобразование Фурье (ДПФ) заключается в поиске другой последовательности x0 , x1 , x2 ,...,xN-1 элементы которой вычисляются по формуле:
(2).
Основным свойством этих преобразований (которое доказывается в соответствующих разделах математики) является тот факт, что из последовательности {x} получается (при прямом преобразовании) последовательность {X}, а если потом применить к {X} обратное преобразование, то снова получится исходная последовательность {x}.
Определение 3 .
Величина
называется поворачивающим множителем .
Рассмотрим ряд свойств поворачивающих множителей, которые нам понадобятся в дальнейшем.
Верхняя цифра в поворачивающем множителе не является индексом, это - степень. Поэтому, когда она равна единице, мы не будем ее писать:
Прямое преобразование Фурье можно выразить через поворачивающие множители. В результате формула (1) примет вид:
(3).
Эти коэффициенты действительно оправдывают свое название. Нарисуем на комплексной плоскости любое комплексное число, в виде вектора, исходящего из начала координат. Представим это комплексное число в показательной форме: rejφ , где r - модуль числа, а φ - аргумент. Модуль соответствует длине вектора, а аргумент - углу поворота:
Теперь возьмем какой-нибудь поворачивающий множитель
.
Его модуль равен единице, а фаза - 2π/N.
Как известно, при умножении комплексных
чисел, представленных в показательной
форме, их модули перемножаются, а
аргументы суммируются. Тогда умножение
исходного числа на поворачивающий
множитель не изменит длину вектора, но
изменит его угол. То есть,
произойдет поворот вектора
на угол 2π/N (см. предыдущий рисунок).
Если теперь посмотреть на формулу (3), то станет ясен геометрический смысл преобразования Фурье: он состоит в том, чтобы представить N комплексных чисел-векторов из набора {x}, каждое в виде суммы векторов из набора {X}, повернутых на углы, кратные 2π/N.
Теорема 0 .
Если комплексное число представлено в виде e j2πN , где N - целое, то это число e j2πN = 1.
Доказательство :
По формуле Эйлера, и ввиду периодичности синуса и косинуса:
e j2 π N = cos(2πN) + j sin(2πN) = cos 0 + j sin 0 = 1 + j0 = 1