Построение гистограммы распределения погрешностей

Указанное построение проводится для качественной проверки соответствия закона распределения погрешностей, полученных при многократных наблюдениях, нормальному закону распределения. Построение гистограммы провести в следующем порядке.

1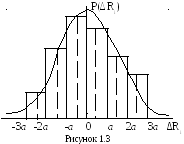Выбрать величину интервала статистического ряда погрешностейа(рис.1.3), для чего по табл.1.1 найти наибольшие по величине остаточные погрешности ∆R_iразных знаков, по их разности определить диапазон наблюдаемых погрешностей b , разделить его на число интервалов r. Тогда интервалa=b/r. Принять r=6. Если b не делится на r точно, то частное округлить до одной–двух значащих цифр.

2 Заполнить таблицу статистического ряда (табл.1.2). Для этого по табл.1.1 подсчитать число S_j остаточных погрешностей, лежащих в интервале 0 –a,а– 2а, 2а– 3аотдельно с плюсом и минусом. Числа S_j записать в табл.1.2. В ту же таблицу внести частоты появления погрешностей, определяемые для каждого интервала как отношение числа погрешностей S_j к общему числу погрешностей n. Погрешности, точно совпадающие по значению с границей интервала, могут быть отнесены либо кj–1 интервалу, либо к j интервалу. Например, если таких погрешностей две, то их целесообразно разделить между смежными интервалами. Для определения высот прямоугольников гистограммы (см. рис.1.3) нужно частоты появления погрешностей разделить на величину интервалов. Вычисленные значения S_j/naвнести в табл.1.2.

Таблица 1.2

Интервалы	0 – a		a – 2a		2a – 3a
Знак погрешностей	+	–	+	–	+	–
Число остаточных погрешностей Sj
Частоты появления погрешностей Sj/n
Высоты прямоугольников гистограммы Sj/na
Середины интервалов ∆Ri
P(∆Ri)

3 Построить гистограмму, для чего по оси абсцисс отложить численные значения интервалов a,2a,3a. На каждом интервале, как на основании построить прямоугольник, площадь которого равна частоте появления погрешностей, лежащих в данном интервале. Значения высот прямоугольников взять из табл.1.2. Площадь гистограммы равна единице (из построения).

4 Построить на том же графике теоретическую кривую нормального распределения в соответствии с уравнением (1.1). Значения P(R_i) определить для точкиR_i= 0 и середин интерваловR_i=a/2;3a/2,5a/2. Полученные значения занести на построенную гистограмму. Соединить нанесенные точки плавной кривой. Сравнить гистограмму с теоретической кривой нормального распределения.