6. Анализ матрицы коэффициентов парной корреляции. Проверка значимости коэффициентов корреляции

Линейный корреляционный анализ позволяет установить прямые связи между переменными величинами по их абсолютным значениям. Формула расчета коэффициента корреляции построена таким образом, что если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона.

В общем виде формула для подсчета коэффициента корреляции такова:

где   - значения, принимаемые переменной X,

 - значения, принимаемые переменой Y,

 - средняя по X,

 - средняя по Y.

Расчет коэффициента корреляции Пирсона предполагает, что переменные   и   распределены нормально.

Матрица парных коэффициентов корреляции представляет собой матрицу, элементами которой являются парные коэффициенты корреляции всех факторов модели.

Для вычисления матрицы коэффициентов парной корреляции R следует воспользоваться инструментом Корреляция. Инструмент Корреляция применяется, если имеется более двух переменных измерений для каждого объекта. В результате выдается таблица, корреляционная матрица, показывающая значение функции КОРРЕЛ для каждой возможной пары переменных измерений. Любое значение коэффициента корреляции должно находиться в диапазоне от -1 до +1 включительно.

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности при использовании множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестаёт быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надёжна оценка распределения суммы объяснённой вариации по отдельным факторам с помощью МНК.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между векторами

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы г_xi,xj (x_i ¹ x_j) были бы равны нулю. Так, для включающего три объясняющих переменных уравнения

y_teor = b₀+b₁×x₁ + b₂×x₂ + b₃×x₃ + ε (5.12)

матрица коэффициентов корреляции между факторами имела бы определитель, равный 1

det(R)=   .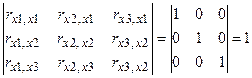

Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции = 1, то определитель такой матрицы равен нулю:

Det(R) =   .

Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадёжнее результаты множественной корреляции. Наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Проверка гипотезы для коэффициента корреляции

Пусть r обозначает выборочный коэффициент корреляции, полученный по извлеченным из двумерного нормального распределения пар наблюдений (x₁, y₁),…,(x_n, y_n).

Коэффициент корреляции   в популяции неизвестен, но может быть оценен по выборке с помощью выборочного коэффициента корреляции r:

 (1)

где оценки среднего равны: 

.

Проверим значимость коэффициента корреляции. 

Нулевая гипотеза состоит в том, что коэффициент корреляции равен нулю, альтернативная - не равен нулю:

Очевидно, достаточно большое по абсолютной величине значение величины r будет стремиться опровергнуть нулевую гипотезу.

Возникает вопрос.

Насколько большое должно быть абсолютное значение величины r?

Для того чтобы проверить гипотезу, мы должны знать распределение величины r.

Собственное распределение величины r довольно сложное, поэтому мы применим преобразование:

      (2)

Итак, выборочное распределение этой статистики есть распределение Стьюдента с n-2 степенями свободы.

При заданном уровне значимости (α) определяем критическое значение t_кр.

Принимаем решение об отклонении или не отклонении нулевой гипотезы:

 - отклоняем H₀

  - не отклоняем H₀

Вычисление уровня значимости коэффициента корреляции

Для определения фактического уровня значимости коэффициента корреляции запишем:

Где Т подчиняется распределению Стьюдента с n-2 степенями свободы, а значение величины t вычисляется в соответствии с формулой (2).

Вычисление уровня значимости эквивалентно определению площади под правым и левым хвостами функции, ограниченной значениями -t и t.