47. Тест Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений: предпосылки, нулевая гипотеза, тестовая статистика, алгоритм

Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j. Т.е. между ними есть зависимость.

Тест Дарбина-Уотсона рассматривает случай взаимного влияния случайных возмущений в соседних наблюдениях:

Cov(u_i,u_j) = 0 ghb j = i - 1

В основе теста лежат следующие предположения:

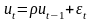- случайные возмущения подчиняютя нормальному закону распределения

- тип автокорреляции - автокорреляция первого порядка

Тест основан на вычислении статистики DW:

i - номер наблюдения

n - кол-во наблюдений

u - значение случайного возмущения

Принято во внимание, что при достаточно больших значениях n, можно записать уравнение следующим образом:

DW = 2(1- p), так как

Для принятия решения относительно наличия или отсутствия автокорреляции нужно понять к какому отрезку относится DW

Если значение попало на отрезки [0; dl] или [4-dl; 4], то гипотеза б отсутствии автокорреляции отклоняется (присутствует автокорреляция). Если на отрезок [du; 4-du], то гипотеза об отсутствии автокорреляции принимается. 2 другие зоны - зоны неопределенности.

Алгоритм:

1)Yоцен = а0оцен +а1оцен*х1t+...

2) Вычисление статистики DW

3) Выбор табличных значений границ критического значения статистики и (по параметрам n, k, )

4) Определение интервала, в который попадает вычисленное значение статистики DW.

48. Тестирование мультиколлинеарности. Метод Фаррара-Глоубера

Если регрессоры в модели связаны строгой функциональной зависимостью, то говорят о наличии полной (совершенной) мультиколинеарности

Полная мультиколлинеарность не позволяет однозначно оценить параметры исходной модели и разделить вклады регрессоров в эндогенную переменную по результатам наблюдений.

Частичная мультиколлинеарность характеризуется коэффициентами парной корреляции между регрессорами, которые так же носят стохастический характер и, по значениям которых судят о степени коррелированности.

Исследование наличия мультиколлинеарности по алгоритму Феррара-Глобера.

Шаг 1. Стандартизация переменных.

Элементы стандартизованных векторов рассчитываются по формулам:

, i=1; n, j=1; m.

где n – число наблюдений;

m – число факторов;

σ_j² – дисперсия j-го фактора.

Поскольку дисперсия рассчитывается по формуле:

,

то формуле для стандартизации переменных примут вид:

, i=1; n, j=1; m.

Шаг 2. Нахождение корреляционной матрицы R (матрицы моментов стандартизованной системы нормальных уравнений).

Корелляционная матрица R определяется по формуле:

R=Х*^Т·Х*,

где Х* – матрица стандартизованных переменных.

Для нахождения элементов корелляционной матрицы R последовательно используем встроенные функции Транспонирование матриц – ТРАНСП и Произведение матриц – МУМНОЖ.

Проверку вычислений следует выполнять, и используя последовательно встроенную функцию КОРРЕЛ, учитывая при этом свойства корреляционной матрицы: корреляционная матрица является симметричной, на главной диагонали расположены единицы.

Шаг 3. Критерий – Х².

Расчетное значение критерия Х² определяется по формуле:

,

где -определитель корреляционной матрицы R-детерминант корреляции.

По заданной доверительной вероятности Р и числу степеней свободы

 находится табличное значение критерия Х²_табл, которое сравнивается с расчетным.

– если Х²_расч< Х²_табл, то нет оснований отклонить гипотезу об отсутствии мультиколлинеарности в массиве факторов, то есть с принятой надежностью можно утверждать, что в массиве факторов мультиколлинеарность отсутствует;

– если Х²_расч> Х²_табл, то гипотеза об отсутствии мультиколлинеарности в массиве факторов отклоняется, то есть с принятой надежностью можно утверждать, что в массиве факторов мультиколлинеарность существует.

Примечание: Если гипотеза об отсутствии мультиколлинеарности в массиве факторов принимается, то исследования мультиколлинеарности останавливаются.