30. Определение структурных изменений в экономике: использование фиктивных переменных, тест Чоу

Если исследователь предполагает, что за время наблюдений произошли резкие структурные изменения в виде связей между зависимой и независимыми переменными, то для проверки этой гипотезы используют тест Чоу. В этом случае строятся три регрессионные модели: первая по наблюдениям, проведенным до изменений, вторая по наблюдениям после происшедших изменений в структуре связей, а третья по всей выборке наблюдений. Нулевая гипотеза состоит в предположении о равенстве истинных соответствующих параметров регрессии для всех моделей. Нулевая гипотеза отвергается при уровне значимости α, если наблюдаемая  -статистика

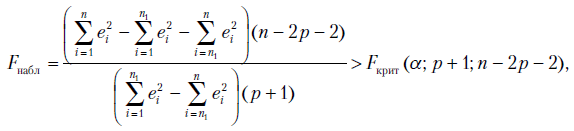, где

	-	число переменных в модели;
	-	суммы квадратов остатков моделей, построенных по наблюдениям, проведенным до изменений, после изменений и по всей выборке.

Наблюдаемая F-статистика Чоу равна

При 

Нулевая гипотеза об отсутствии изменения в тенденции поведения ряда урожайности в России после распада СССР уверенно опровергается на 1%-ном уровне значимости.

Тест Чоу на наличие структурных изменений в регрессионной модели.

Тест Г. Чоу изначально разработан для тех случаев, когда имеется две выборки значений, одна из которых (объемом n) получена при одних условиях, другая (m) – при несколько измененных. При этом необходимо выяснить, действительно ли выборки однородны (гипотеза H0). Критерий также может быть использован при построении регрессионных моделей при воздействии качественных признаков, когда имеется возможность разделения совокупности наблюдений по степени воздействия признака на отдельные группы и требуется установить возможность использования единой модели регрессии.

Механизм теста: по каждой выборке строятся регрессионные модели:

В противном случае гипотеза о совпадении моделей для обеих выборок не отклоняется, т.е. влияние качественного признака на исследуемую выборку несущественно и их можно объединить в одну.

31. Основные числовые характеристики вектора остатков в классической множественной регрессионной модели. Оценка дисперсии возмущений модели множественной регрессии

Для определения автоковариационной матрицы вектора оценок параметров множественной регрессии необходимо оценить дисперсию возмущений 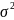. Оценка дисперсии возмущений выражается через сумму квадратов остатков регрессии:

, где

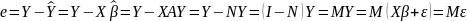
n – мерный вектор-столбец остатков регрессии – случайный вектор (функция выборочных данных). Матица М ( как и матрица N) идемподентная и симметричная.

Определим количественные характеристики случайного вектора 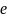. Относительно вектора принимаются следующие предпосылки- условия Гаусса:

1. Математическое ожидание возмущения равно нулю (математическое ожидание вектора возмущений есть нулевой вектор размера n)

2. Дисперсия возмущений всегда одинакова для всех наблюдений результата Y (Это условие называется условием гомоскедастичности)

3. Возмущения не коррелированы между собой (ковариация между отдельными возмущениями равна нулю)

Вектор математических ожиданий для остатков регрессии:

Автоковариационная матрица вектора остатков определяется по правилу

в силу идемпотентности матрицы М. Несмещенной оценкой дисперсии возмущений множественной регрессии является оценка вида:

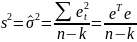
где k- число параметров модели (столбцов матрицы регрессоров).