2. Алгоритм обработки результатов пфэ

1. В каждой строке матрицы планирования рассчитываются среднее значениепоmпараллельным опытам ипострочная или выборочнаядисперсия:

,i = 1,2,..., N. (11)

,i = 1,2,..., N. (12)

2. Проверяетсяоднородностьвыборочных дисперсий покритерию Кохрена:

, (13)

полученное значение сравнивается с табличным .– числа степеней свободы, по которым определяется табличное значение.¹Если, то дисперсии однородны. Это означает, что все опыты были проведены с одинаковой точностью и расчет может быть продолжен. Если гипотеза об однородности дисперсий не подтверждается, то одними из решений являются увеличение числа параллельных опытов, изменение метода контроля выходной переменной, масштабирование выходной переменной.

3. Определяется ошибка опыта или дисперсия воспроизводимости:

. (14)

4. Коэффициенты уравнения регрессии определяются по формуле:

(15)

где n – число столбцов матрицы планирования.

Для оценки значимости коэффициента b_jвычисляется его дисперсия – одинаковое значение для всех коэффициентов:

(16)

и расчетное значение критерия Стьюдента:

(17)

Если тоj–ый коэффициент считаетсязначимым, еслито коэффициент принимается равным нулю, т.е. соответствующий фактор или взаимодействие факторов исключается из уравнения регрессии. Исключение незначимого коэффициента не скажется на других коэффициентах, при этом выборочные коэффициентыоказываются так называемыми несмешанными оценками для соответствующих коэффициентов генеральной совокупности, т.е. коэффициенты уравнения регрессии характеризуют вклад каждого фактора и взаимодействия факторов в выходную величину. Причины незначимости коэффициентов уравнения регрессии могут быть следующие: 1) факторвключен в рассмотрение ошибочно и он не влияет на выходной параметрY; 2) выбран слишком малый интервал варьирования.

5. После того, как уравнение регрессии получено в окончательном виде, проверяется его адекватность. Для этого рассчитывается дисперсия адекватности:

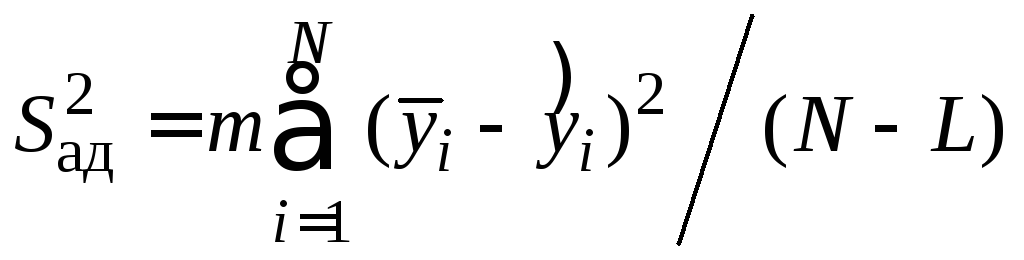. (18)

Здесь – значение выходного параметра, рассчитанное по полученному уравнению регрессии,L– число значимых коэффициентов в уравнении регрессии. Затем рассчитывается значения критерия Фишера:

(19)

Если то полученное уравнение адекватно описывает исследуемый процесс. При неадекватности модели наиболее часто принимают решение об уменьшении интервала варьирования факторов и повторении эксперимента. Такое решение, хотя и уменьшает кривизну поверхности отклика, однако, может привести к появлению незначимых коэффициентов. Очень эффективно включать в план эксперимента новый фактор из числа отсеянных при предварительных экспериментах.

3. Раскодировка уравнения регрессии

Пусть в результате обработки результатов ПФЭ (табл. 2) получено уравнение регрессии:

Факторы входят в него в кодированном виде. Чтобы получить уравнение в натуральном масштабе, воспользуемся формулами (4):

После подстановки получим

4. Особый случай проведения пфэ с параллельными опытами в одной точке факторного пространства.

Этот план проведения эксперимента применяется в тех случаях, когда объект исследуется не впервые и заранее известна хорошая воспроизводимость результатов, а значит нет острой необходимости проводить параллельные опыты для каждой строки матрицы планирования. В этих случаях достаточно выполнить три–четыре опыта в центре плана, т.е. при значениях факторов, равных основному или нулевому уровню, или в другой точке исследуемой области факторного пространства.

Ошибка опыта рассчитывается по формуле

(20)

где 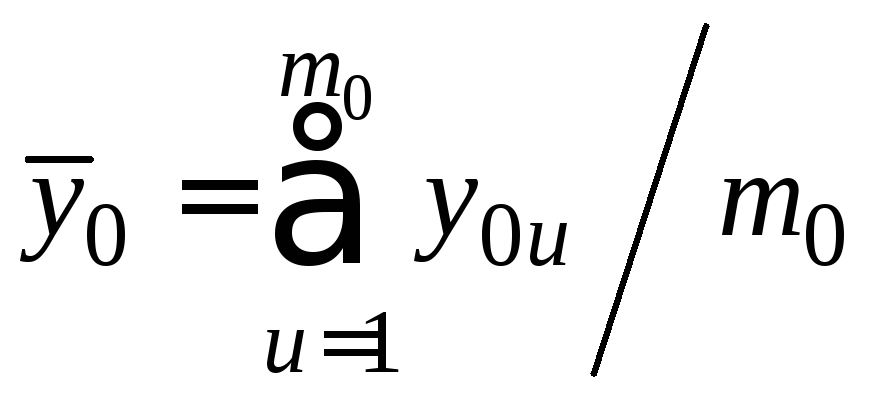;– значения выходного параметра в параллельных опытах,– число проведенных в одной точке параллельных опытов.

Алгоритм обработки результатов в этом случае представляет собой пп.4, 5 из алгоритма обработки результатов ПФЭ. При этом в расчетные формулы необходимо внести следующие изменения

, (21)

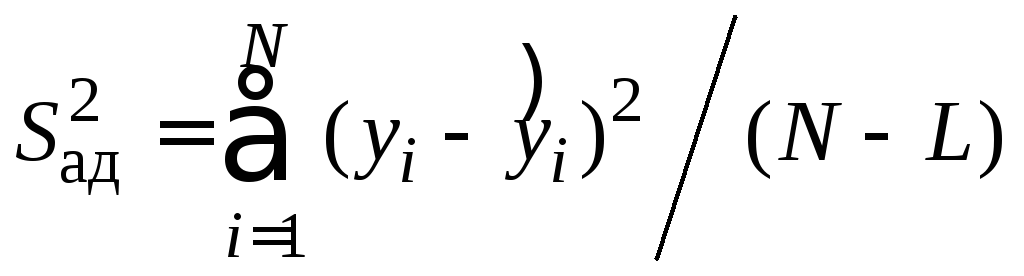. (22)

Число степеней свободы для определения табличных значений критериев Стьюдента и Фишера .