2.3. Полный заряд в полупроводнике при заданном поверхностном потенциале

Ограничимся рассмотрением приближения невырожденного электронного газа. Это приближение хорошо выполняется в режиме обеднения и слабой инверсии и вполне удовлетворительно описывает ситуацию сильной инверсии, соответствующую вырожденным носителям.

Одномерное уравнение Пуассона для объема полупроводника p-типа имеет вид:

. (2.3.1)

Нас интересует случай обеднения и инверсии, когда . С учетом (2.1.1), (2.1.2) и пренебрегая концентрацией дырок, имеем следующее приближение для плотности заряда в правой части уравнения Пуассона:

,

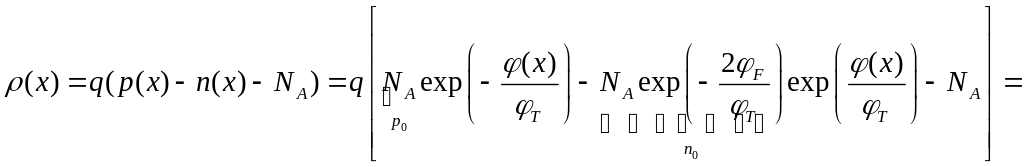
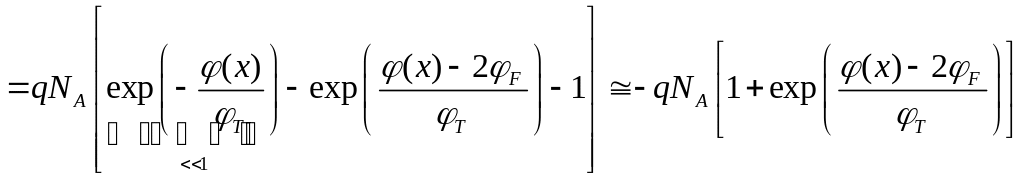где мы пренебрегли концентрацией дырок.

Уравнение Пуассона принимает вид

. (2.3.2)

Умножим обе стороны уравнения (2.3.2) на . Используя тождество и переменную , имеющую смысл электрического поля, проинтегрируем обе стороны уравнения от границы раздела кремния с изолятором, где электрическое поле равно искомому полю , а потенциал равен поверхностному потенциалу , до границы обедненного слоя, где электрическое поле и потенциал равны нулю:

.

Получаем зависимость электрического поля от потенциала:

. (2.3.3)

Отсюда в точке находим связь электрического поля на границе раздела и поверхностного потенциала :

, (2.3.4)

где введено обозначение для безразмерной функции

(2.3.5)

и для характерной длины задачи, которой является дебаева длина экранирования

. (2.3.6)

Тогда электрическое поле в кремнии на границе раздела

, (2.3.7)

а полная поверхностная (Кл/см²) плотность заряда в полупроводнике для заданного потенциала

. (2.3.8)

В общем случае уравнение (2.3.3) нужно решать численно, чтобы найти . В частных случаях можно сделать некоторые приближения, позволяющие решить интеграл аналитически. Например, в приближении полного обеднения, когда, в квадратных скобках уравнений (2.3.3) и (2.3.8) требуется сохранить только член, ответственный за заряд неподвижных акцепторов . В приближении сильной инверсии, наоборот, требуется сохранить только экспоненциальный член , ответственный за заряд в инверсионном слое (канале). Таким образом, в предельных случаях сильной инверсии и глубокого обеднения:

(2.3.9)

В общем случае после наступления сильной инверсии член , представляющий инверсионный заряд в (2.3.3), должен быть сохранен вместе с членом, представляющим заряд обеднения:

Это уравнение может быть решено только численно с граничным условием: . После нахождения можно найти распределение в инверсионном слое по формуле (2.1.2а). Пример численного расчета представлен на рис.2.4 для двух значений при . Распределение электронов чрезвычайно близко к поверхности с толщиной инверсионного слоя меньше 50Å. Более высокий поверхностный потенциал приводит к ещё более тонкому слою инверсионного заряда вблизи поверхности. Вообще электроны в инверсионном слое должны рассматриваться квантовомеханически как двумерный газ. Как будет показано на семинаре, посвященном квантовым эффектам, электроны инверсионного слоя занимают дискретные энергетические уровни и имеют пиковое значение плотности на расстоянии 10-20Å от поверхности.

Рис.2.4. Распределение электронов инверсного слоя для двух значений поверхностного потенциала [4]