3. Приклади розв’язання задач

1. Зразок виконання задачі 1 − Розрахунок валу редуктора

Дано:

Приведення сил до осі валу редуктора.

Точка .

Після приведення в точці знаходяться поперечні сили : – паралельно осі,– паралельно осі; поздовжня силата моменти

–згинальний в площині ,

–крутний в площині .

Точка .

Після приведення в точці знаходяться поперечні сили:– паралельно осі,– паралельно осі; поздовжня силата моменти

–згинальний в площині ,

–крутний в площині .

Точка .

Після приведення в точці знаходяться поперечні сили– паралельно осі,– паралельно осі; поздовжня силаи моменти

–згинальний в площині ,

–крутний в площині .

Згин у вертикальній площині (YOZ)

Визначення реакцій

Перевірка:

Побудова епюри згинальних моментів :

Згин в горизонтальній площині (XOZ)

Визначення реакцій

Перевірка:

Побудова епюри згинальних моментів :

Кручення (XOY)

Перевірка рівноваги валу:

Побудова епюри крутних моментів :

Розтягання – стискання

Визначення реакції :

Побудова епюри поздовжніх сил :

Визначення небезпечного перерізу вала редуктора

Допустиме напруження:

Внутрішні зусилля в перерізах:

Переріз К .

Переріз B .

Переріз (зліва).

Переріз (справа).

Переріз (справа).

Переріз L .

Еквівалентні моменти в перерізах:

–небезпечний переріз (справа).

Визначення діаметру вала з умови міцності в першому приближенні (без урахування поздовжньої сили).

З умови міцності згідно IV гіпотези маємо:

Приймаємо збільшений до найближчого стандартного значення діаметр – (див. п. 1.2.6).

Перевірка міцності валу з урахуванням дії поздовжньої сили

Визначаємо геометричні характеристики перерізу:

Максимальні напруження в перерізі (справа)

Перевіримо виконання умови міцності:

Перевіримо переріз (справа) з максимальною поздовжньою силою.

Перевіримо виконання умови міцності в перерізі (справа)

Остаточно приймаємо

2. Зразок виконання задачі 2 − Розрахунок просторового брусу

Дано:

Побудова епюр внутрішніх силових факторів

• ділянка DK.

Вважаємо, що ділянка DK жорстко закріплена в точці D.

Вирази для внутрішніх силових факторів:

• згинальний момент:

Епюра згинального моменту будується в площині (YOZ), на стислих волокнах.

• поперечна сила:

• ділянка СD.

Вважаємо, що ділянка СD жорстко закріплена в точці С. Силу приводимо до точкиD з додатковим моментом в площині .

Вирази для внутрішніх силових факторів:

• згинальні моменти:

Епюри згинальних моментів будуються у відповідних площинах, на стислих волокнах.

• поперечні сили:

• крутний момент:

• ділянка BC.

Вважаємо, що ділянка BC жорстко закріплена в точці B. Всі навантаження з точки D приводимо до точки С. При цьому виникають додаткові моменти в площині від дії сили та в площині від дії сили . Момент переноситься вздовж осі без змін.

Вирази для внутрішніх силових факторів:

• згинальні моменти:

Епюри згинальних моментів будуються у відповідних площинах, на стислих волокнах.

• поперечні сили:

• поздовжня сила:

• крутний момент:

• ділянка LB.

Вважаємо, що ділянка LB жорстко закріплена в точці B.

Вирази для внутрішніх силових факторів:

• згинальний момент:

Епюра згинального моменту будується в площині (YOZ) на стислих волокнах.

• поперечна сила:

• ділянка OB.

Ділянка OB жорстко закріплена в точці O. Всі навантаження переносимо в точку B з точок С та L.

Силу приводимо до точкиB з додатковим моментом в площині .

Сила приводиться до точкиB з додатковим моментом в площині .

При приведенні сили до точкиB виникає додатковий момент в площині .

Моменти , , та сила переносяться вздовж осіZ без змін.

Моменти, що лежать в одній площині алгебраїчно просумуються:

в площині ;

в площині .

Сума сил тапозначається як.

Вирази для внутрішніх силових факторів:

• згинальні моменти:

Епюри згинальних моментів будуються у відповідних площинах, на стислих волокнах.

• поперечні сили:

• поздовжня сила:

• крутний момент:

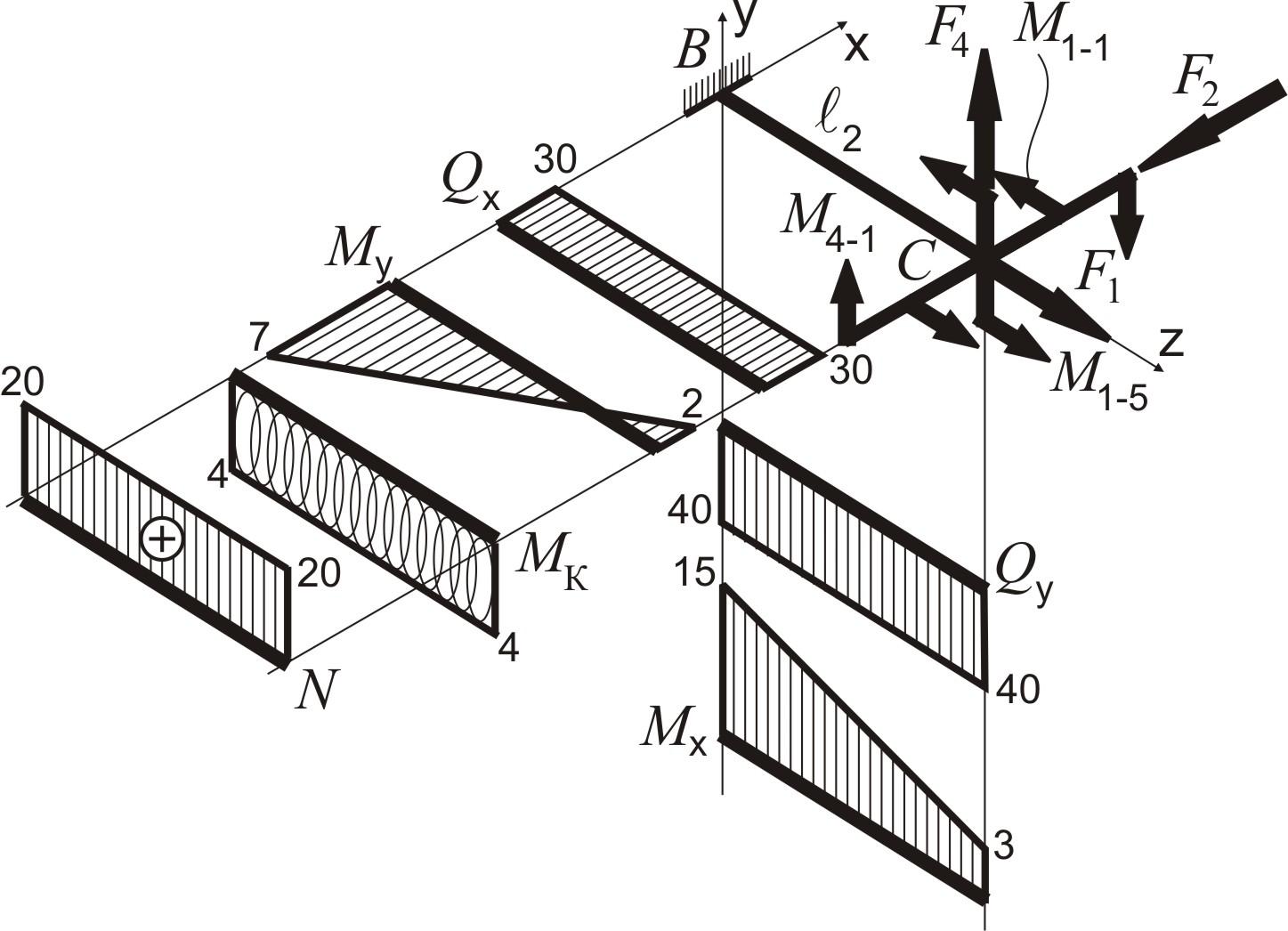
Епюри внутрішніх силових факторів просторового бруса:

• згинальний момент

• поперечні сили

• крутний момент

• поздовжня сила

Внутрішні зусилля в небезпечному перерізі ОО:

Визначення геометричних характеристик поперечного перерізу

Визначення максимальних значень компонент напружень

Побудова епюр напружень в поперечному перерізі

Визначення найнебезпечнішої точки поперечного перерізу

Підраховуємо еквівалентні напруження у восьми характерних точках небезпечного перерізу ОО:

Точка 1

Напружений стан – лінійний (одновісний)

Точка 2

Напружений стан – плоский (двовісний).

Точка 3

Напружений стан – лінійний (одновісний)

Точка 4

Напружений стан – плоский (двовісний).

Точка 5

Напружений стан – лінійний (одновісний)

Точка 6

Напружений стан – плоский (двовісний).

Точка 7

Напружений стан – лінійний (одновісний)

Точка 8

Напружений стан – плоский (двовісний).

Визначення коефіцієнта запасу

–умова міцності виконується.