
Ryadi_Novyy
.docРяди.
В цьому розділі розглядається розв’язання типових прикладів з теми «Ряди» (ряди числові, функціональні, Фур’є та їх застосування), надається список рекомендованої літератури [2, 3, 6, 9, 13, 16], пропонується 30 варіантів розрахунково-графічних завдань (РГЗ), які складаються із 12 прикладів. Перед виконанням варіанту РГЗ студент повинен вивчити відповідний теоретичний матеріал по цій темі і вміти відповісти на контрольні питання, які пропонуються.
Контрольні питання.
-
Дайте означення числового ряду. Який ряд називається збіжним, розбіжним?
-
Необхідна умова збіжності рядів.
-
Ознаки порівняння рядів з додатними членами.
-
Інтегральна ознака Коші.
-
Ознака Даламбера.
-
Радикальна ознака Коші.
-
Ознака збіжності ряду з довільними членами. Умовна та абсолютна збіжність.
-
Знакопереміжний ряд. Умова Лейбніця.
-
Функціональний ряд. Точка його збіжності.
-
Область збіжності функціонального ряду. Як використовують ознаку Даламбера та радикальну ознаку Коші для знаходження області збіжності функціональних рядів?
-
Степеневі ряди. Теорема Абеля. Радіус збіжності степеневого ряду.
-
Ряди Тейлора та Маклорена.
-
Записати ряд Маклорена для таких функцій:
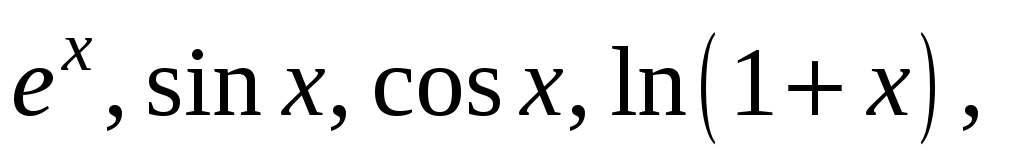

-
Означення ряду Фур’є. Теорема Діріхле.
-
Розкладання в ряд Фур’є парних і непарних функцій.
Розв’язування типових прикладів.
Приклад 1.
Дослідити
ряд
 на збіжність.
на збіжність.
Розв’язання.
Скористаємось необхідною
ознакою збіжності,
за якою, якщо ряд
![]() збігається, то
збігається, то
![]() .
Але, якщо
.
Але, якщо
![]() ,
то ряд розбігається.
Обчислимо
,
то ряд розбігається.
Обчислимо
![]() ,
з цього випливає, що ряд розбігається,
так як не виконана необхідна умова
збіжності.
,
з цього випливає, що ряд розбігається,
так як не виконана необхідна умова
збіжності.
Відповідь: ряд розбігається.
Приклад 2.
Дослідити
ряд
 на збіжність.
на збіжність.
Розв’язання. Скористаємось інтегральною ознакою Коші:
якщо
функція
![]() неперервна, додатна, не зростаюча для
неперервна, додатна, не зростаюча для
![]() і
і
![]() для всіх
для всіх
![]() ,
то справедливо наступне: 1) із збіжності
невласного інтегралу
,
то справедливо наступне: 1) із збіжності
невласного інтегралу
 випливає збіжність ряду
випливає збіжність ряду![]() ;
2) із розбіжності невласного інтегралу
;
2) із розбіжності невласного інтегралу
 випливає розбіжність ряду
випливає розбіжність ряду
![]() .
.
Треба
зауважити, що нижньою межею інтегрування
в інтегралі
 може бути будь-яке додатне число із
області існування функції.
може бути будь-яке додатне число із
області існування функції.
Для заданого ряду умови ознаки Коші виконуються. Дослідимо на збіжність відповідний ряду невласний інтеграл:

З цього випливає , що невласний інтеграл збігається, а , значить, і ряд збігається.
Відповідь: ряд збігається.
Приклад 3.
Дослідити
ряд
 на збіжність.
на збіжність.
Розв'язання.
Скористаємось ознакою
порівняння в граничній формі:
якщо існує скінченна границя
 ,
то ряди
,
то ряди
![]() і
і
![]() з додатними членами поводять себе
однаково (збігаються або розбігаються
одночасно).
Для
порівняння часто використовують наступні
ряди:
з додатними членами поводять себе
однаково (збігаються або розбігаються
одночасно).
Для
порівняння часто використовують наступні
ряди:
а) б)
б)
 Для
порівняння візьмемо ряд
Для
порівняння візьмемо ряд
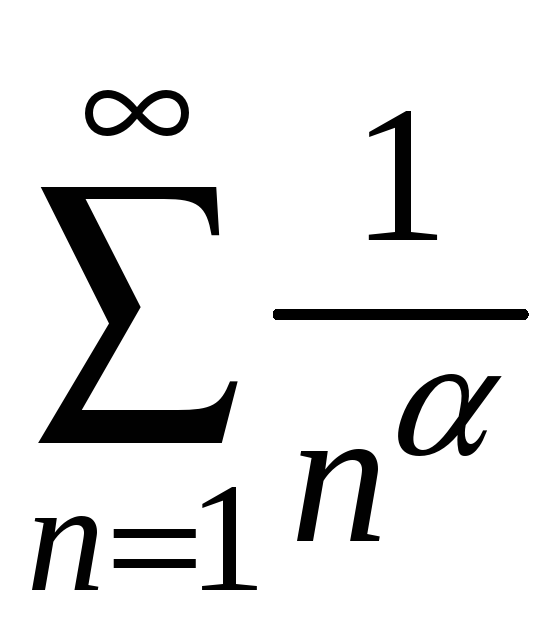 .
Обчислимо границю:
.
Обчислимо границю:

 ,
,
якщо
![]() ,
а
так як
,
а
так як
 –
збігається, то збігається і вихідний
ряд.
–
збігається, то збігається і вихідний
ряд.
Відповідь: ряд збігається.
Приклад 4.
Дослідити
ряд
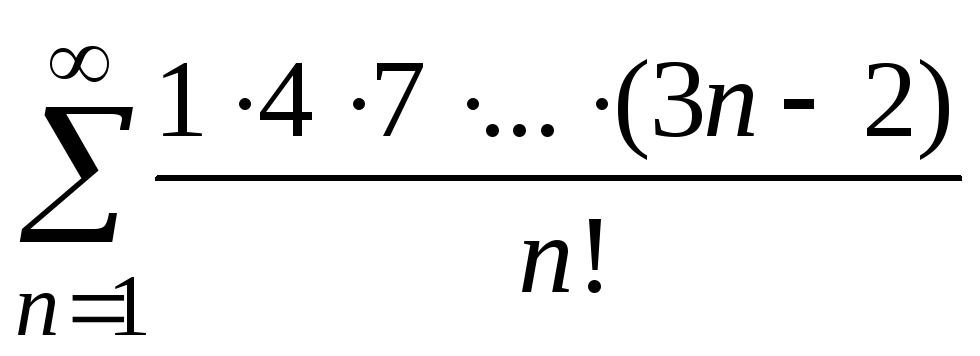 на збіжність.
на збіжність.
Розв'язання.
Скористаємось ознакою
Даламбера:
якщо для ряду
![]() з додатними членами існує скінченна
границя
з додатними членами існує скінченна
границя
 ,
тоді: 1) якщо
,
тоді: 1) якщо
![]() ,
то ряд
,
то ряд
![]() збігається; 2) якщо
збігається; 2) якщо
![]() ,
то ряд
,
то ряд
![]() розбігається; 3) якщо
розбігається; 3) якщо
![]() ,
то ознака відповіді не дає, потрібні
додаткові дослідження.
,
то ознака відповіді не дає, потрібні
додаткові дослідження.
Обчислимо границю:
 .
.
З цього випливає, що вихідний ряд розбігається.
Відповідь: ряд розбігається.
Приклад
5.
Дослідити ряд
 на збіжність.
на збіжність.
Розв'язання.
Скористаємось радикальною
ознакою Коші:
якщо для ряду з додатними членами
![]() існує скінченна границя
існує скінченна границя
![]() ,
тоді: 1) якщо
,
тоді: 1) якщо
![]() ,
то ряд
,
то ряд
![]() збігається; 2) якщо
збігається; 2) якщо
![]() ,
то ряд
,
то ряд
![]() розбігається; 3) якщо
розбігається; 3) якщо
![]() ,
то ознака відповіді не дає, потрібні
додаткові дослідження.
,
то ознака відповіді не дає, потрібні
додаткові дослідження.
Обчислимо границю:
 .
.
З цього випливає, що вихідний ряд збігається.
Відповідь: ряд збігається.
Приклад
6. Дослідити
ряд
 на збіжність.
на збіжність.
Розв'язання.
Заданий ряд є знакопереміжним.
Скористаємось достатньою ознакою
збіжності рядів з довільними членами.
Складемо ряд із абсолютних величин
вихідного ряду:
 .
Отриманий ряд є ряд з додатними членами,
тому можна скористатись ознакою
порівняння в граничній формі.
Для
порівняння візьмемо збіжний ряд
.
Отриманий ряд є ряд з додатними членами,
тому можна скористатись ознакою
порівняння в граничній формі.
Для
порівняння візьмемо збіжний ряд
![]() і обчислимо границю:
і обчислимо границю:
 .
.
Таким чином, ряд, складений із абсолютних величин вихідного ряду, збігається, а тому вихідний ряд збігається абсолютно.
Відповідь: ряд збігається абсолютно.
Приклад
7. Дослідити
ряд
 на збіжність.
на збіжність.
Розв'язання.
Заданий ряд є знакопереміжним. Перевіримо
необхідну умову збіжності ряду.
Для
цього знайдемо
![]() .
Необхідна умова не виконується, тому
що
.
Необхідна умова не виконується, тому
що
![]() ,
а, значить, ряд розбігається.
,
а, значить, ряд розбігається.
Відповідь: ряд розбігається.
Приклад
8.
Дослідити ряд
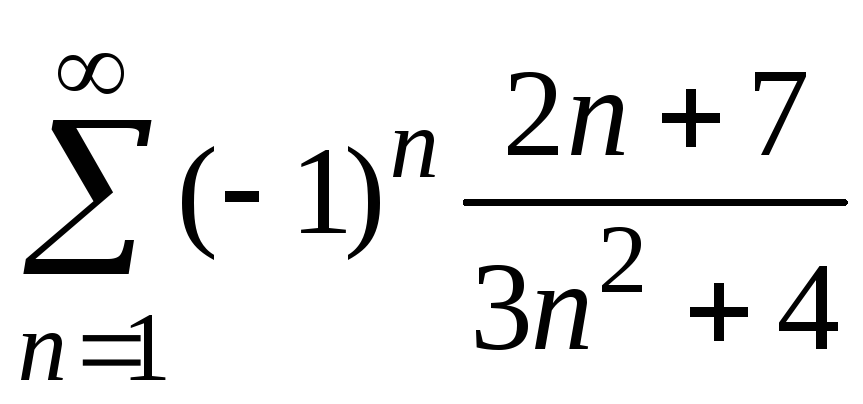 на збіжність.
на збіжність.
Розв'язання.
Заданий ряд є знакопереміжним. Складемо
ряд із абсолютних величин вихідного
ряду:
 .
Отриманий ряд є рядом з додатними
членами, скористаємось ознакою порівняння
в граничній формі.
Для
порівняння візьмемо розбіжний ряд
.
Отриманий ряд є рядом з додатними
членами, скористаємось ознакою порівняння
в граничній формі.
Для
порівняння візьмемо розбіжний ряд
![]() .
Обчислимо границю:
.
Обчислимо границю:
 ,
тому ряд із абсолютних величин
розбігається. Це означає, що вихідний
ряд не є абсолютно збіжним. Перевіримо
вихідний ряд на умовну збіжність.
Скористаємось
ознакою
Лейбніця:
якщо члени ряду
,
тому ряд із абсолютних величин
розбігається. Це означає, що вихідний
ряд не є абсолютно збіжним. Перевіримо
вихідний ряд на умовну збіжність.
Скористаємось
ознакою
Лейбніця:
якщо члени ряду
 ,
задовольняють умовам: 1)
,
задовольняють умовам: 1)
![]() 2)
2)
![]() ,
тоді ряд збігається і його сума
,
тоді ряд збігається і його сума
![]() .
.
Перевіримо виконання умов ознаки Лейбніця.
Перша
умова:
![]() виконується
тому, що
виконується
тому, що

 ,
отже
,
отже
 для будь-якого
для будь-якого
![]() .
.
Друга
умова: теж виконується, тому за ознакою Лейбніця
ряд збігається. Так як абсолютної
збіжності вихідний ряд немає, то він
збігається умовно.
теж виконується, тому за ознакою Лейбніця
ряд збігається. Так як абсолютної
збіжності вихідний ряд немає, то він
збігається умовно.
Відповідь: ряд збігається умовно.
Приклад
9. Знайти
область збіжності функціонального ряду
 .
.
Розв'язання.
Складемо ряд із абсолютних величин
вихідного ряду:
 ,
так як
,
так як
![]()
![]() ,
і скористаємось радикальною
ознакою Коші.
Обчислимо границю
,
і скористаємось радикальною
ознакою Коші.
Обчислимо границю
![]() .
За ознакою Коші цей ряд збігається, коли
.
За ознакою Коші цей ряд збігається, коли
![]() ,
тобто, коли
,
тобто, коли
![]() .
.
Перевіримо
цей ряд на збіжність, коли
![]() ,
тобто при
,
тобто при
![]() .
Отриманий при
.
Отриманий при
![]() числовий ряд має вигляд:
числовий ряд має вигляд:
 .
Цей ряд розбігається, так як для нього
не виконується необхідна умова збіжності.
Отже, область збіжності вихідного ряду
є
.
Цей ряд розбігається, так як для нього
не виконується необхідна умова збіжності.
Отже, область збіжності вихідного ряду
є
![]() .
.
Відповідь:
![]() .
.
Приклад
10. Знайти
область збіжності функціонального ряду
 .
.
Розв'язання. Скористаймось ознакою Даламбера для ряду, складеного із абсолютних величин вихідного ряду. Обчислимо границю:
 .
.
Для всіх
х,
що задовольняють нерівність
![]() ,
ряд розбігається, а для всіх х,
що задовольняють нерівність
,
ряд розбігається, а для всіх х,
що задовольняють нерівність
![]() ,
ряд збігається, тобто для
,
ряд збігається, тобто для
![]() .
Перевіримо
на збіжність ряд в точках
.
Перевіримо
на збіжність ряд в точках
![]() і
і
![]() .
.
Числовий
ряд, відповідний
![]() :
:
 .
Цей ряд збігається за ознакою Лейбніця.
.
Цей ряд збігається за ознакою Лейбніця.
Числовий
ряд, відповідний
![]() ,
має вигляд:
,
має вигляд:
 .
Цей ряд розбіжний. Отже область збіжності
вихідного ряду [1; 5).
.
Цей ряд розбіжний. Отже область збіжності
вихідного ряду [1; 5).
Відповідь: [1; 5).
Приклад
11.
Знайти радіус та область збіжності ряду
 .
Розв'язання.
Заданий функціональний ряд є степеневим.
Знайдемо його радіус збіжності за
формулою
.
Розв'язання.
Заданий функціональний ряд є степеневим.
Знайдемо його радіус збіжності за
формулою
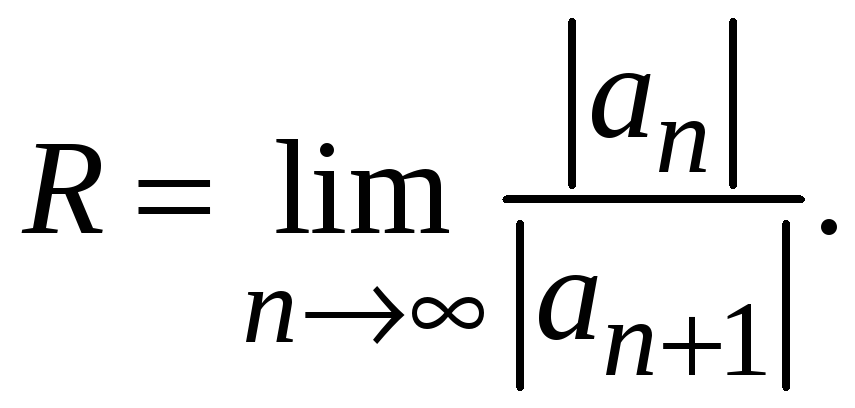 Таким чином,
Таким чином,
 .
.
Вихідний
ряд збігається для всіх х,
що задовольняють нерівність
![]() ,
або
,
або
![]() .
Перевіримо ряд на збіжність в точках,
які є кінцями інтервалу збіжності.
.
Перевіримо ряд на збіжність в точках,
які є кінцями інтервалу збіжності.
Числовий
ряд, відповідний
![]() ,
має вигляд:
,
має вигляд:
![]() і збігається. Отже,
і збігається. Отже,
![]() є точкою збіжності ряду.
є точкою збіжності ряду.
Числовий
ряд, відповідний
![]() ,
має вигляд
,
має вигляд
 і теж збігається, більш того, абсолютно.
Отже, і
і теж збігається, більш того, абсолютно.
Отже, і
![]() є точкою збіжності ряду. Таким чином,
область збіжності вихідного ряду є
є точкою збіжності ряду. Таким чином,
область збіжності вихідного ряду є
![]() .
.
Відповідь:
![]() ,
,
![]() .
.
Приклад
12.
Розкласти
функцію
![]() в ряд Тейлора в околі точки
в ряд Тейлора в околі точки
![]() і вказати область збіжності ряду.
і вказати область збіжності ряду.
Розв'язання. Відомо, що

а
областю збіжності цього ряду є інтервал
![]() .
Перетворимо задану функцію таким чином:
.
Перетворимо задану функцію таким чином:
![]() .
Замінимо
.
Замінимо
![]() та одержимо:
та одержимо:
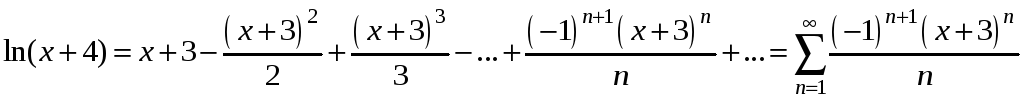 .
.
Отриманий
ряд збігається, якщо![]() ,
або
,
або
![]() .
Отже
.
Отже
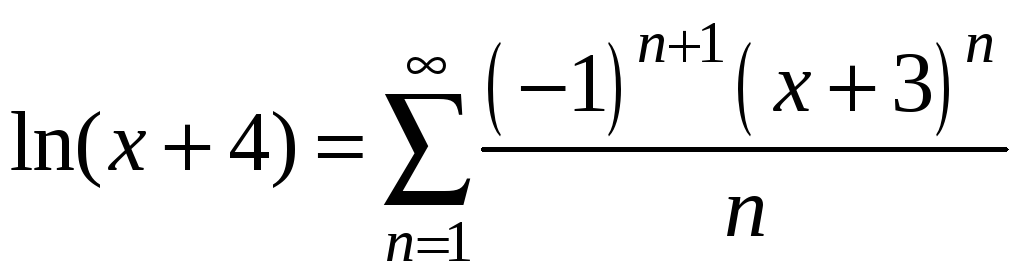 ,
а область збіжності -
,
а область збіжності -
![]() .
.
Відповідь:
 ,
,
![]() .
.
Приклад
13.
Розкласти
функцію
![]() в ряд Маклорена і вказати область
збіжності ряду.
в ряд Маклорена і вказати область
збіжності ряду.
Розв'язання. Відомо, що:

![]() .
.
Замінимо
![]() та одержимо:
та одержимо:

 ,
,![]() .
.
Відповідь:
 ,
,
![]() .
.
Приклад
14.
Обчислити
наближено
 з точністю до
з точністю до
![]() .
.
Розв'язання.
Використаємо розкладання в ряд Маклорена
функції
![]() :
:
 ,
,
![]() .
.
Тоді:
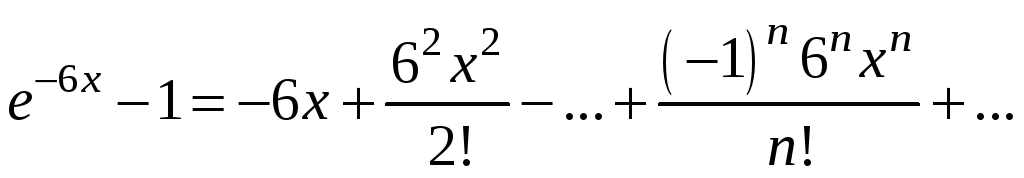 ,
,
![]() .
.

 .
.
Задана
точність виконана, так як
![]() .
.
Відповідь:![]() .
.
Приклад 15. Знайти чотири перших, відмінних від нуля, члени розкладу в степеневий ряд розв’язання диференціального рівняння:
![]()
Розв'язання.
Припустимо, що розв'язок цього рівняння
може бути у вигляді
 де
де
![]()
Розв'яжемо
це рівняння відносно
![]() :
:
![]() де
де
![]() Знайдемо
Знайдемо
![]() :
:
![]() .
.
Тоді:
![]() звідки
звідки
![]()
При
необхідності можна продовжувати
диференціювання
попередньо отриманого рівняння далі.
Таким
чином,
![]()
Відповідь:
![]()
П риклад
16.
Розкласти
в ряд Фур'є періодичну функцію періоду
риклад
16.
Розкласти
в ряд Фур'є періодичну функцію періоду
![]() ,
задану на проміжку
,
задану на проміжку
![]() :
:

Графік
цієї функції зображено на рис.1. Якщо
функція має період
![]() ,
то її ряд Фур'є має вигляд: Рис.1.
,
то її ряд Фур'є має вигляд: Рис.1.
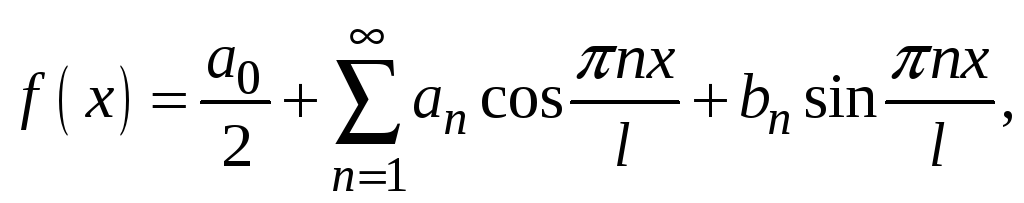
де


Розв'язання.
У нашому випадку
![]() .
Обчислимо коефіцієнти ряду Фур'є:
.
Обчислимо коефіцієнти ряду Фур'є:
 .
.

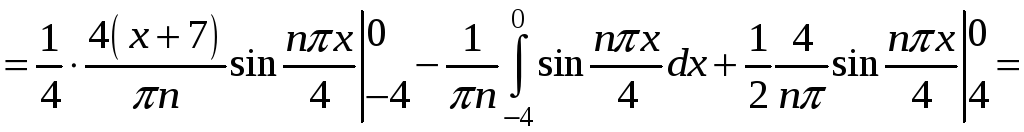

![]() Таким чином:
Таким чином:




![]()

Отже,
 .
.
Відповідь:
 .
.
Приклад
17.
Розкласти
в ряд Фур'є за синусами функцію
![]() ,
задану на проміжку
,
задану на проміжку
![]() .
.
Розв'язання. Для розкладання в ряд Фур'є неперіодичних функцій, заданих у певному скінченому проміжку, її періодично продовжують. Отриману в результаті періодичну функцію розкладають в ряд Фур'є. Цей ряд дає шукане розкладання, так як на заданому проміжку обидві функції (вихідна та періодично продовжена) співпадають.
П родовжимо
задану функцію на проміжок
родовжимо
задану функцію на проміжок
![]() непарно,
а на всю числову пряму - періодично з
періодом
непарно,
а на всю числову пряму - періодично з
періодом
![]() .
Графік такої функції зображено на рис.2
.
Ряд
Фур'є за синусами має вигляд:
.
Графік такої функції зображено на рис.2
.
Ряд
Фур'є за синусами має вигляд:
 де
де
 У
нашому випадку
У
нашому випадку
![]() .
Тоді:
.
Тоді:
 Рис.2.
Рис.2.

![]()

Отже,

 .
.
Відповідь:

Завдання 1. Дослідити ряд на збіжність:
1.
 .
.
2.
 .
.
3.
 .
.
4.
 .
.
5.
 .
.
6.
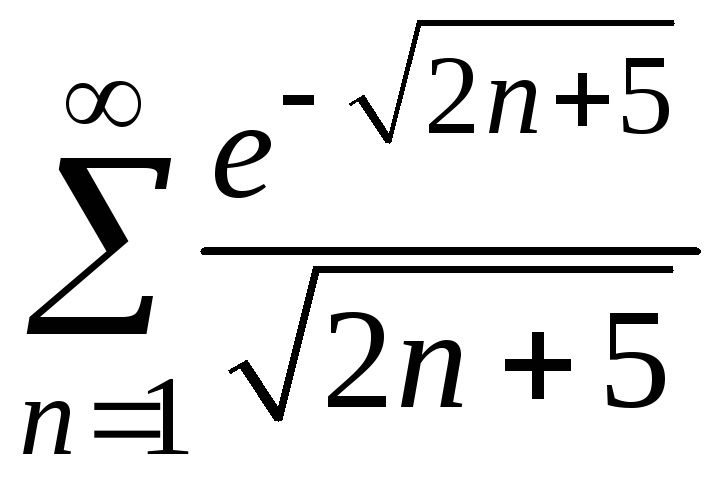 .
.
7.
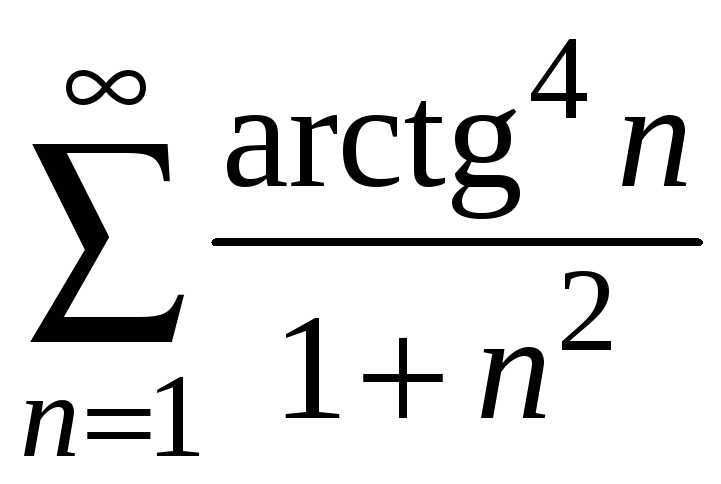 .
.
8.
 .
.
9.
 .
.
10.
 .
.
11.
 .
.
12.
 .
.
13.
 .
.
14.
 .
.
15.
 .
.
16.
 .
.
17.
 .
.
18.
 .
.
19.
 .
.
20.
 .
.
21.
 .
.
22.
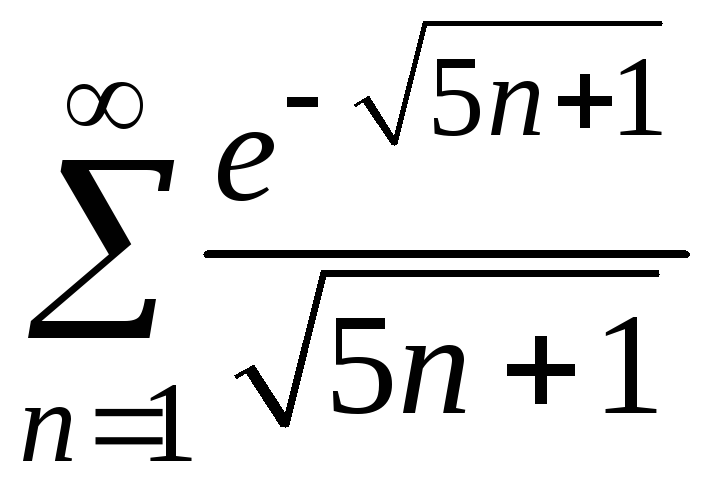 .
.
23.
 .
.
24.
 .
.
25.
 .
.
26.
 .
.
27.
 .
.
28.
 .
.
29.
 .
.
30.
 .
.
Завдання 2. Дослідити ряд на збіжність:
1. .
.
2.
 .
.
3.
 .
.
4.
 .
.
5.
 .
.
6.
 .
.
7.
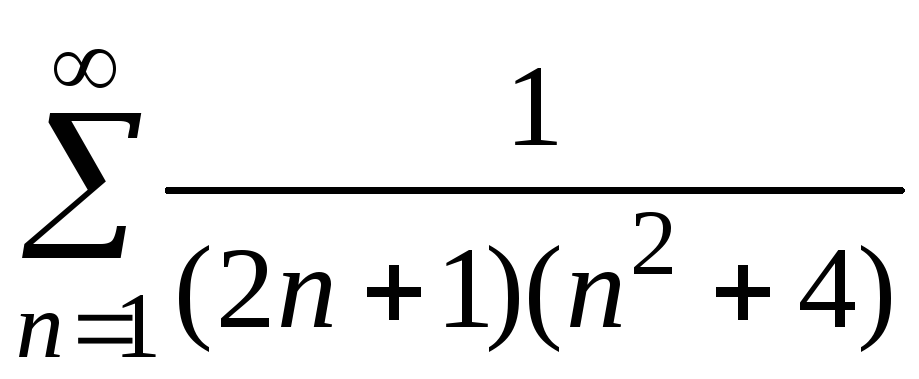 .
.
8.
 .
.
9.
 .
.
10.
 .
.
11.
 .
.
12.
 .
.
13.
 .
.
14.
 .
.
15.
 .
.
16.
 .
.
17.
 .
.
18.
 .
.
19.
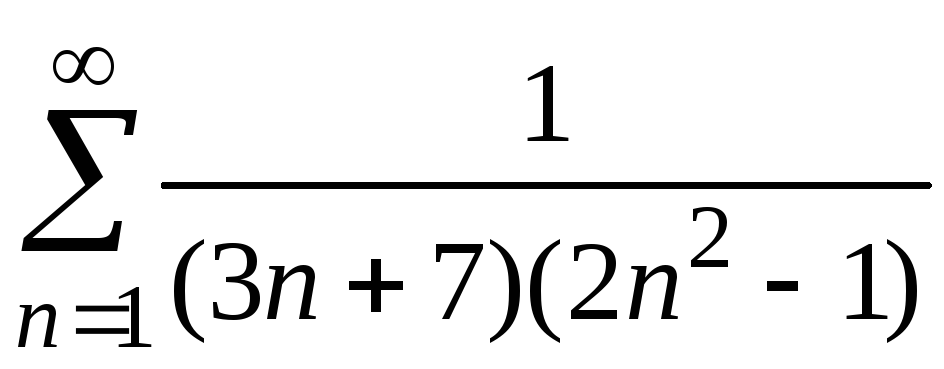 .
.
20.
 .
.
21.
 .
.
22.
 .
.
23.
 .
.
24.
 .
.
25.
 .
.
26.
 .
.
27.
 .
.
28.
 .
.
29.
 .
.
30.
 .
.
Завдання 3. Дослідити ряд на збіжність:
1.
 .
.
2.
![]() .
.
