Вариант 23

1. Найти все решения уравнения и построить их на комплексной плоскости.

2. Зная, что один из корней уравнения равен , найти остальные корни.

3. Найти фундаментальную систему решений и записать общее решение системы

4. Доказать, что если координаты векторов х и у указаны в ортонормированном базисе, то их скалярное произведение выражается через координаты по формуле: . Как выражается скалярное произведение векторов в ортогональном, но не нормированном базисе ?

5. В базисе пространства многочленов не выше второй степени линейный оператор задан матрицей . Найти матрицу этого оператора в базисе полиномов Лежандра: .

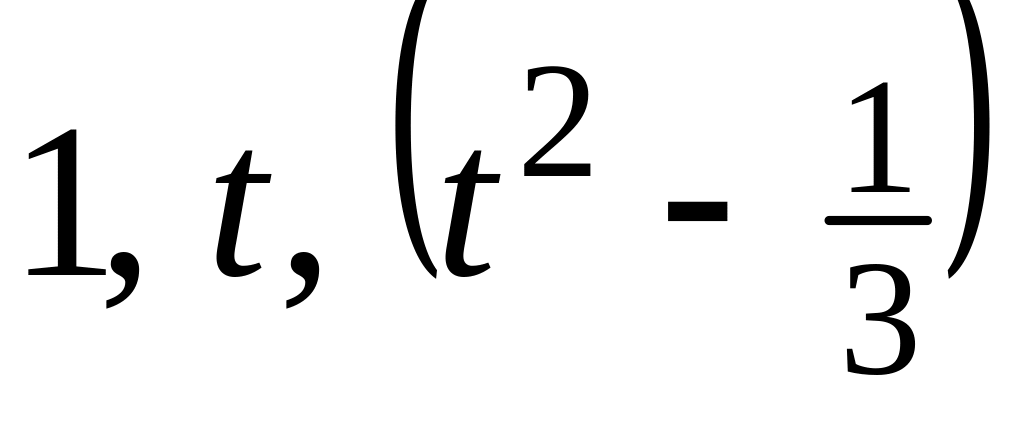6. Найти вещественные собственные числа и соответствующие собственные векторы матрицы

7. Привести уравнение кривой 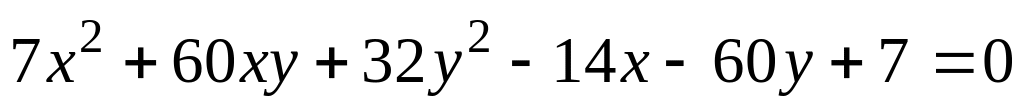к каноническому виду, указать преобразование координат и изобразить на чертеже относительно старых и новых осей координат.

Вариант 24

1. Вычислить . Изобразить результат на комплексной плоскости.

2. Решить уравнение .

3. Найти фундаментальную систему решений и записать общее решение системы через фундаментальную систему решений

4. Доказать, что преобразование трехмерного пространства , где , является линейным преобразованием и найти его матрицы в ортонормированном базисе , в котором даны координаты всех векторов , и в базисе .

5. Исследовать линейную зависимость системы векторов 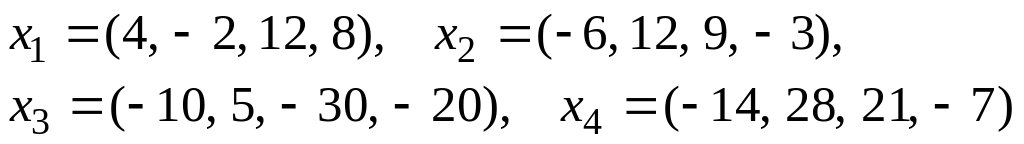Найти какую-нибудь базу этой системы и выразить через базу все остальные векторы системы.

6. Найти собственные числа и собственные векторы матрицы. Привести матрицу к диагональному виду.

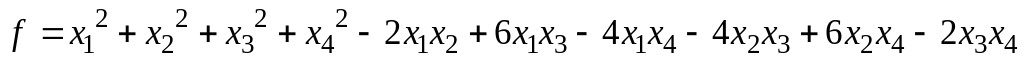7. Привести квадратичную форму к каноническому виду. Указать линейное преобразование, осуществляющее это приведение и тип формы.

Вариант 25

1. Найти все решения уравнения .

2. Определить кратность корня для уравнения .

3. Найти фундаментальную систему решений и записать общее решение системы

4. В пространстве многочленов не выше второй степени задано скалярное произведение по правилу: , где 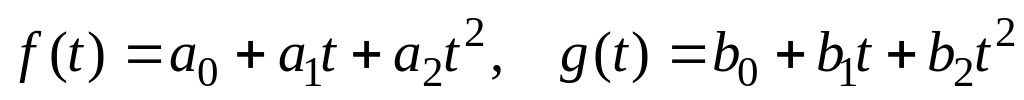. Найти матрицу оператора дифференцирования в базисе , в базисе , , и в базисе

5. Проверить, что векторы образуют базис трехмерного арифметического пространства. Построить по заданному базису ортогональный и ортонормированный базис того же пространства.

6. Найти вещественные собственные числа и соответствующие собственные векторы матрицы

7. Привести уравнение кривой к каноническому виду, указать преобразование координат и изобразить на чертеже относительно старых и новых осей координат.

Вариант 26

1. Вычислить .

2. При каких значениях а и b многочлен делится на ?

3. Найти фундаментальную систему решений и записать общее решение системы через фундаментальную систему решений

4. Из определения сопряженного оператора вывести следующие свойства: 1) (А*)* 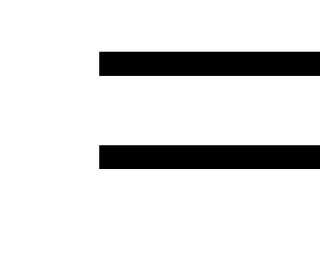А; 2) (А+В)* А*+В*; 3) (αА)*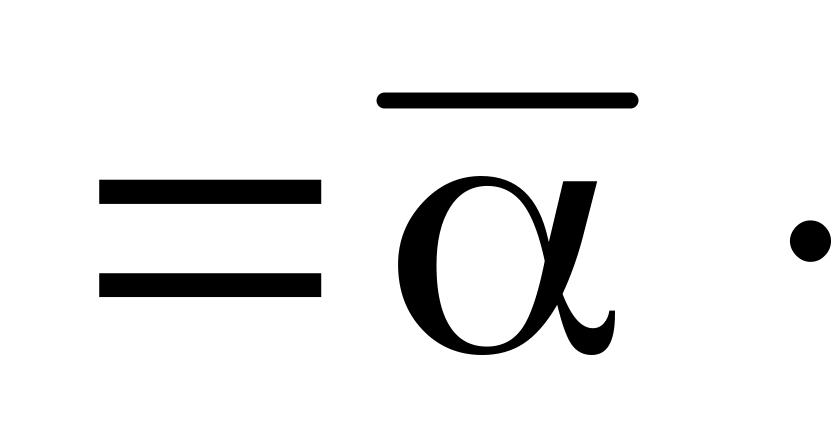 А*; 4) (АВ)* В*А*; 5) Если А ― невырожденный оператор, то (А^-1)* (А*)^-1.

5. Исследовать линейную зависимость системы векторов Найти какую-нибудь базу этой системы и выразить через базу все остальные векторы системы.

6. Найти вещественные собственные числа и соответствующие собственные векторы матрицы.

7. Привести квадратичную форму к каноническому виду. Указать линейное преобразование, осуществляющее это приведение и тип формы.