Вариант 1

1. Найти все значения и показать их на комплексной плоскости.

2. Найти кратность корня (―2) для многочлена .

3. Найти фундаментальную систему решений и записать общее решение системы

4. Рассмотрим систему тригонометрических функций: 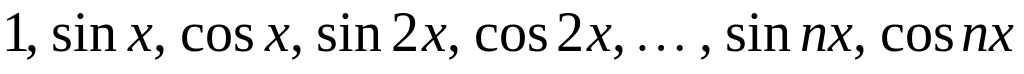. Тригонометрическим многочленом степени называется линейная комбинация функций тригонометрической системы . Доказать, что множество всех тригонометрических многочленов степени не выше 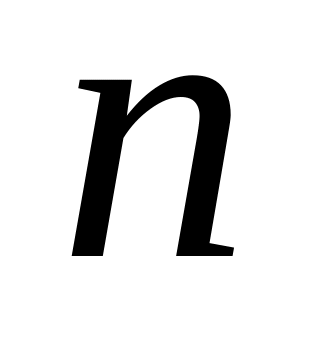является линейным пространством, а система тригонометрических функций ― базисом пространства. Указать размерность пространства и его нулевой элемент.

5. Матрица линейного оператора в некотором базисе имеет вид Найти матрицу этого оператора в базисе , если

6. Найти собственные числа и собственные векторы матрицы

7. Привести уравнение кривой к каноническому виду. Изобразить на чертеже в старой и новой системах координат.

Вариант 2

1. Вычислить и показать результат на комплексной плоскости.

2. Построить многочлен наименьшей степени по его корням: двойной корень 1, простые корни 2, 3, .

3. Найти фундаментальную систему решений и записать общее решение системы

4. Пусть ― произвольный многочлен вещественного аргумента t степени не выше четвертой. Доказать, что оператор является линейным и найти его матрицу в базисе .

5. Исследовать линейную зависимость системы векторов Найти какую-нибудь базу этой системы и выразить через базу все остальные векторы системы.

6. Найти собственные числа и собственные векторы матрицы

7. Привести квадратичную форму к каноническому виду, указать ее тип и линейное преобразование, приводящее ее к каноническому виду.

Вариант 3

1. Найти все значения и показать их на комплексной плоскости.

2. Определить и так, чтобы трехчлен делился на .

3. Найти фундаментальную систему решений и записать общее решение системы через фундаментальную систему решений

4. Рассмотрим систему тригонометрических функций: . Тригонометрическим многочленом степени называется линейная комбинация функций тригонометрической системы . Определим скалярное произведение в пространстве тригонометрических многочленов степени по формуле . Доказать, что введенное число обладает всеми свойствами скалярного произведения. Показать, что система тригонометрических функций составляет ортогональный базис пространства многочленов при . Составить ортонормированный базис.

5. Как изменится матрица перехода от базиса к базису 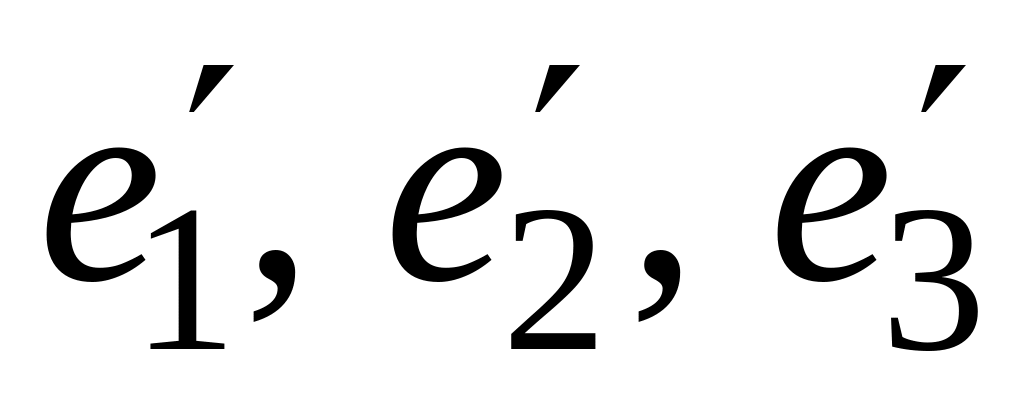, если 1) переставить векторы и ? 2) переставить векторы и ?

6. Найти собственные числа и собственные векторы матрицы. Привести матрицу к диагональному виду

7. Привести уравнение кривой к каноническому виду, указать преобразование координат. Изобразить на чертеже в старой и новой системах координат.

Вариант 4