Дисциплина: Системы статистического анализа данных Лабораторная работа №5 Непараметрические критерии
Непараметрические методы позволяют исследовать данные без каких-либо допущений о характере распределения переменных, в том числе – при нарушении требования нормальности распределения.
В лабораторной работе будут использованы следующие непараметрические критерии:
Сравнение двух независимых выборок (критерий Манна–Уитни)позволяет установить различия между двумя независимыми выборками по уровню выраженности порядковой переменной.
Сравнение двух независимых выборок (критерий серий Вальда - Вольфовица)предназначен для проверки нулевой гипотезы о равенстве целого ряда параметров двух выборок, включая медианы и коэффициенты асимметрии.
Сравнение двух связанных (зависимых) выборок может проводиться по двум критериям. Критерий знаковоснован на подсчете числа отрицательных и положительных разностей между повторными измерениями;критерий Уилкоксона в дополнение к знакам разностей учитывает их величину.
Критерий серийопределяет, является ли последовательность бинарных величин (событий) случайной или упорядоченной.
Критерий Колмогорова—Смирновадля одной выборки определяет отличие распределения переменной от нормального (равномерного, Пуассона и т. д.).
Сравнение К независимых выборок (критерий Н Крускала—Уоллеса)позволяет установить степень различия между тремя и более независимыми выборками по уровню выраженности порядковой переменной.
Сравнение К связанных (зависимых) выборок (критерий Фридмана)позволяет установить степень различия между тремя и более зависимыми выборками по уровню выраженности порядковой переменной.
1. Реализация в spss
1.1. Сравнение независимых выборок
1.1.1.Критерий Манна-Уитни (Mann-Whitney) u-критерий
Критерий Манна-Уитни, так же как и t-критерий для независимых выборок, позволяет выявить существенность разницы между средними значениями выборок. Разница заключается в том, чтоt-критерий ориентирован на нормальное распределение, аU-критерий – на распределения, отличные от нормальных.
При реализации метода, программа сначала ранжирует все объекты без учета принадлежности к сравниваемым группам, а затем вычисляет средние ранги для каждой из двух групп. После нахождения средних рангов определяется p-уровень (уровень значимости).
Для сравнения двух независимых выборок с помощью U-критериянеобходимо использовать следующую последовательность команд:
Analyze (Анализ) - Nonparametric Tests (Непараметрические критерии) – Legacy Dialogs (Устаревшие диалоги) - 2 Independent Samples (Две независимые группы)
В результате на экране появится диалоговое окно (рис.1), в котором необходимо задать в поле Test Variable Listпеременные, которые подлежат проверке, а в полеGrouping Variables– группирующую переменную.
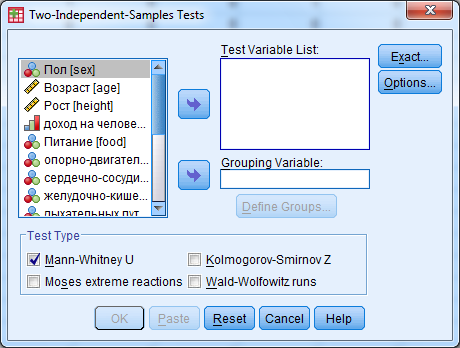
Рис.1. Диалоговое окно Two Independent Samples Tests
Чтобы рассчитать критерий Манна – Уитни для двух независимых выборок необходимо установить флажок в поле Mann-Whitney U. После щелчка на кнопкеОКна экран будет выведен результат теста.
На рис.2. представлено сравнение средних значений индекса массы тела до программы похудения для мужчин и женщин
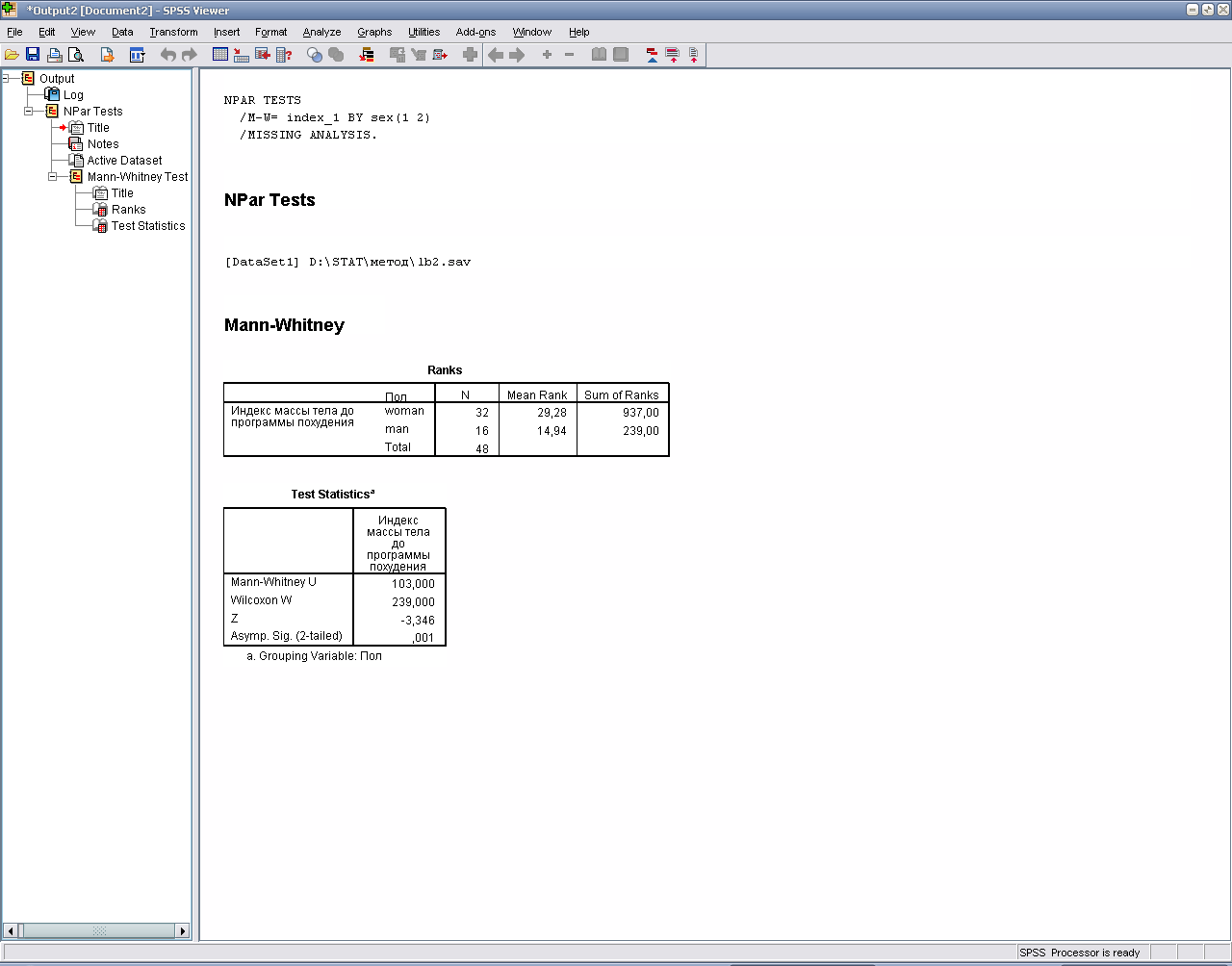
Рис.2.Пример расчетаU-критерия Манна-Уитни
Результаты теста говорят о значимом различии между индексами массы тела для мужчин и женщин (р=0,001<0,05).