2.2. Применение t-критерия для зависимых выборок

Для того, чтобы сравнить средние двух зависимых выборок необходимо использовать следующую последовательность команд:

Statistics (Статистики) – Basic Statistics and Tables (Основные статистики и таблицы) - t-test, dependent samples (t-критерий для зависимых выборок)

В результате откроется диалоговое окно (рис.17.), в котором необходимо указать пару переменных для сравнения средних.

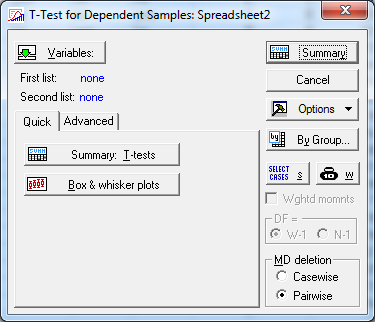
Рис.17.ДиалоговоеокноT-Test for Dependent Samples

После нажатия на кнопку Summary на экран будет выведена таблица результатов вычисления t-критерия.

Пример сравнения средних двух зависимых переменных index_1 и index_2 представлен на рис.18. Соответствующая коробчатая диаграмма приведена на рис.19.

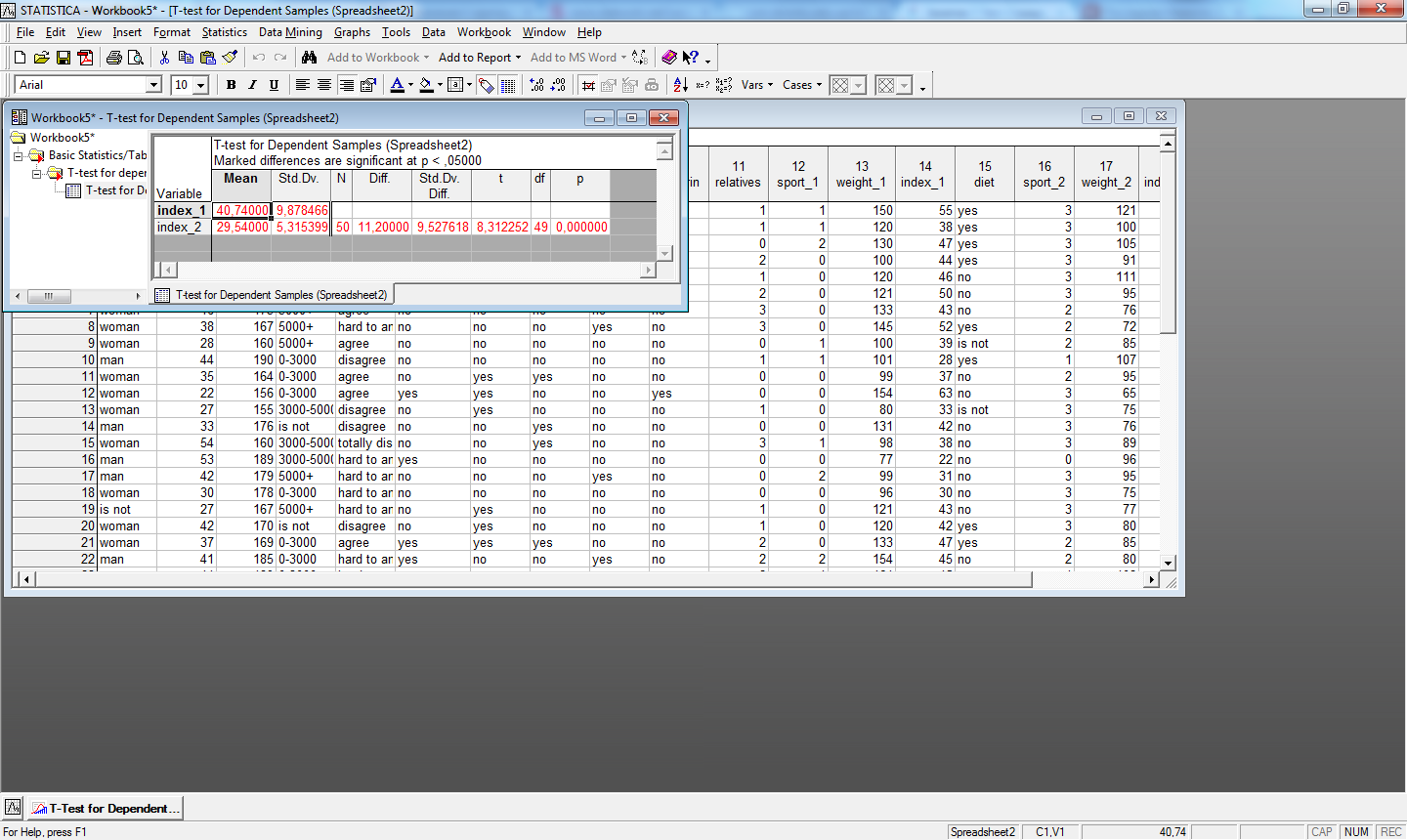
Рис.18. Применение t-критерия для зависимых выборок

(сравнение средних двух переменных)

Как видно из результатов, для выборки объемом N = 50 среднее значение переменной index_1 (40,7400) оказалось статистически значимо выше среднего значения переменной index_2 (29,5400) с уровнем значимости p < 0,001.

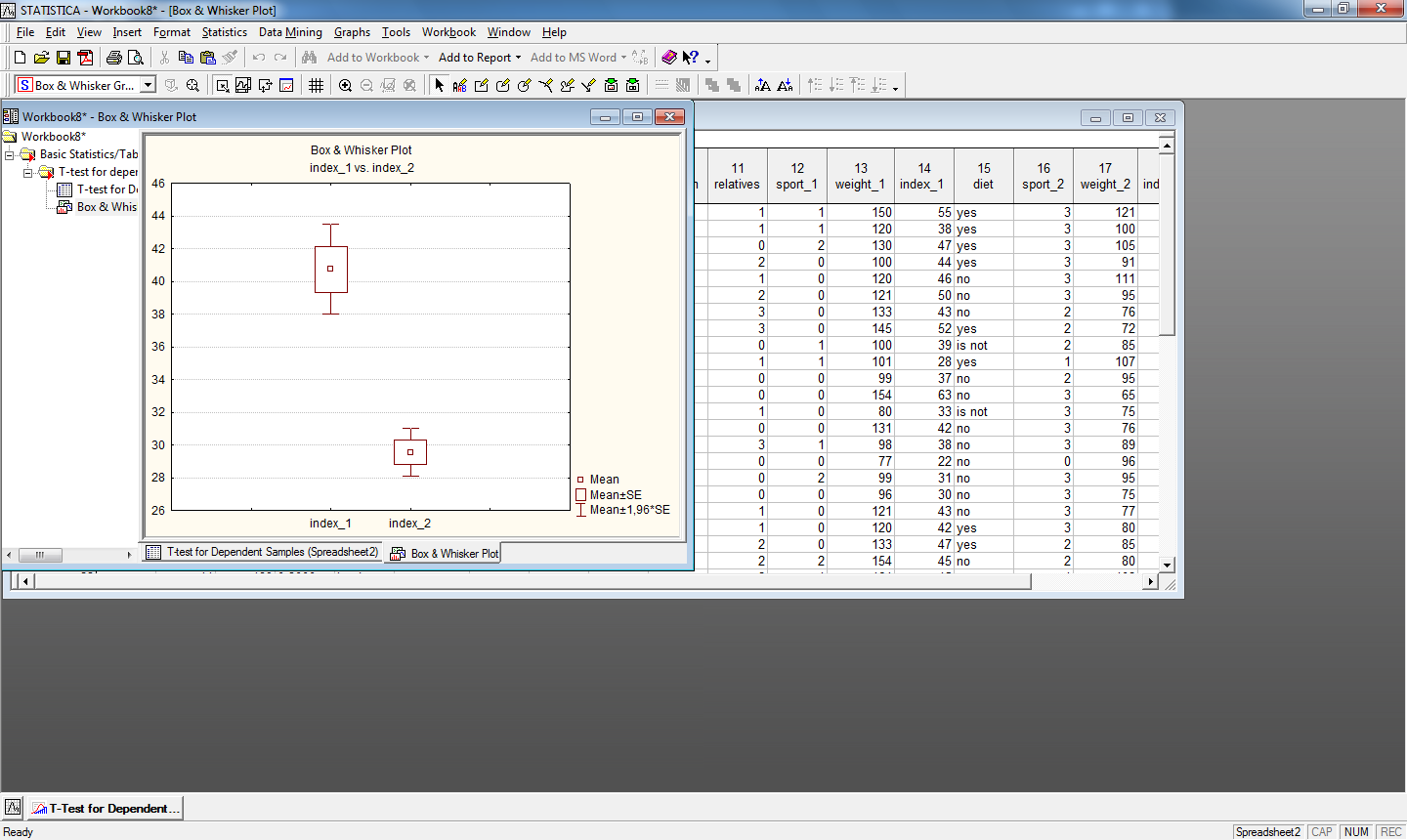
Рис.19. Коробчатая диаграмма для зависимых переменных index_1 и index_2

Существует возможность проводить вычисления t-критерия по группам. Для этого в диалоговом окне T-Test for Dependent Samples (рис.17.) необходимо щелкнуть на кнопку By Group (По группам) и в открывшемся диалоговом окне (рис.20) указать группирующую переменную и нажать кнопку ОК.

Рис.20. Диалоговое окно By Group

После нажатия кнопки Summary на экран будет выведено окно с результатами вычисления t-критерия. Окно будет содержать несколько таблиц. Первая – All Groups (Все группы), далее для каждой группы в отдельности.

Пример сравнения средних двух зависимых переменных index_1 и index_2, сгруппированных по переменной пол представлен на рис.21.

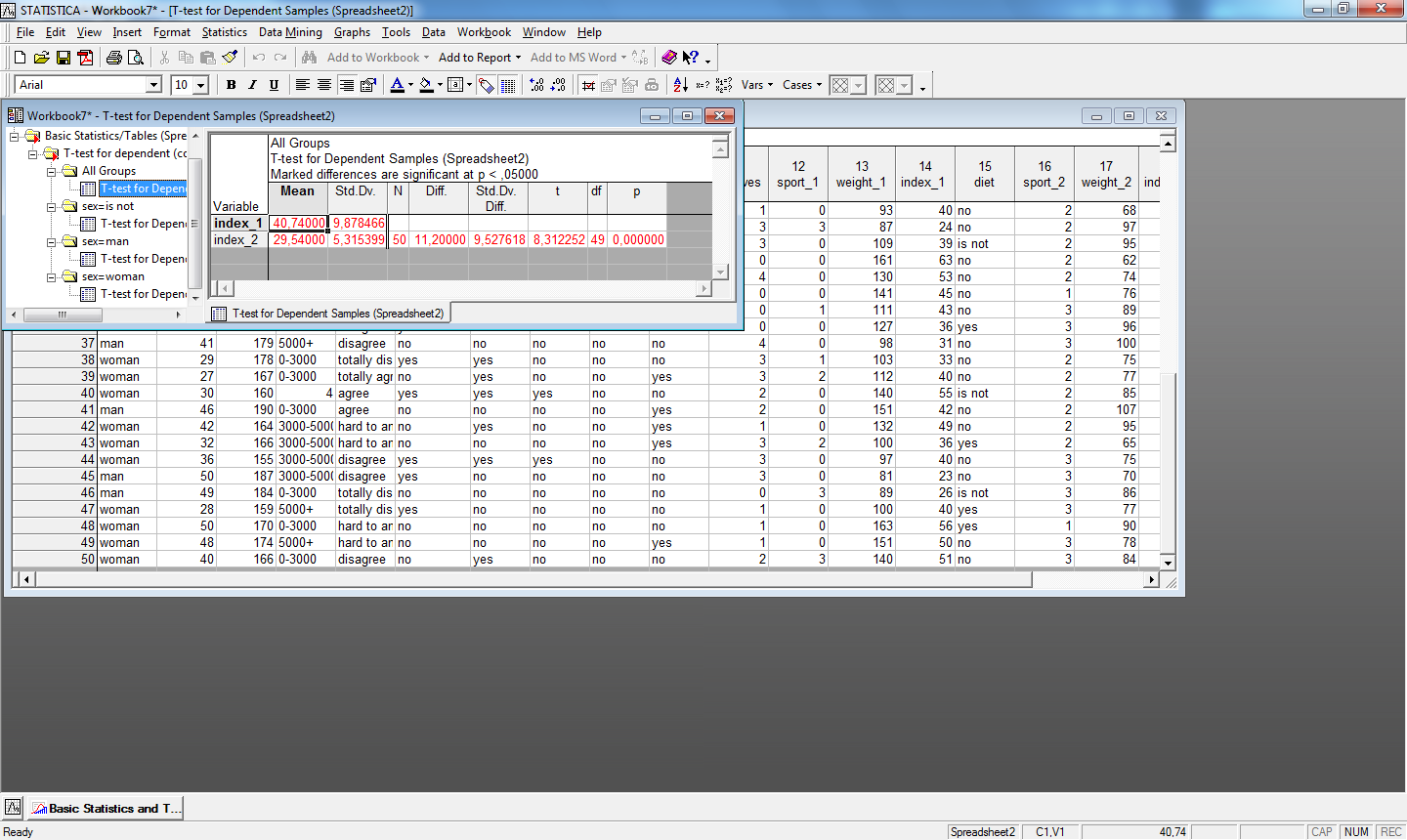
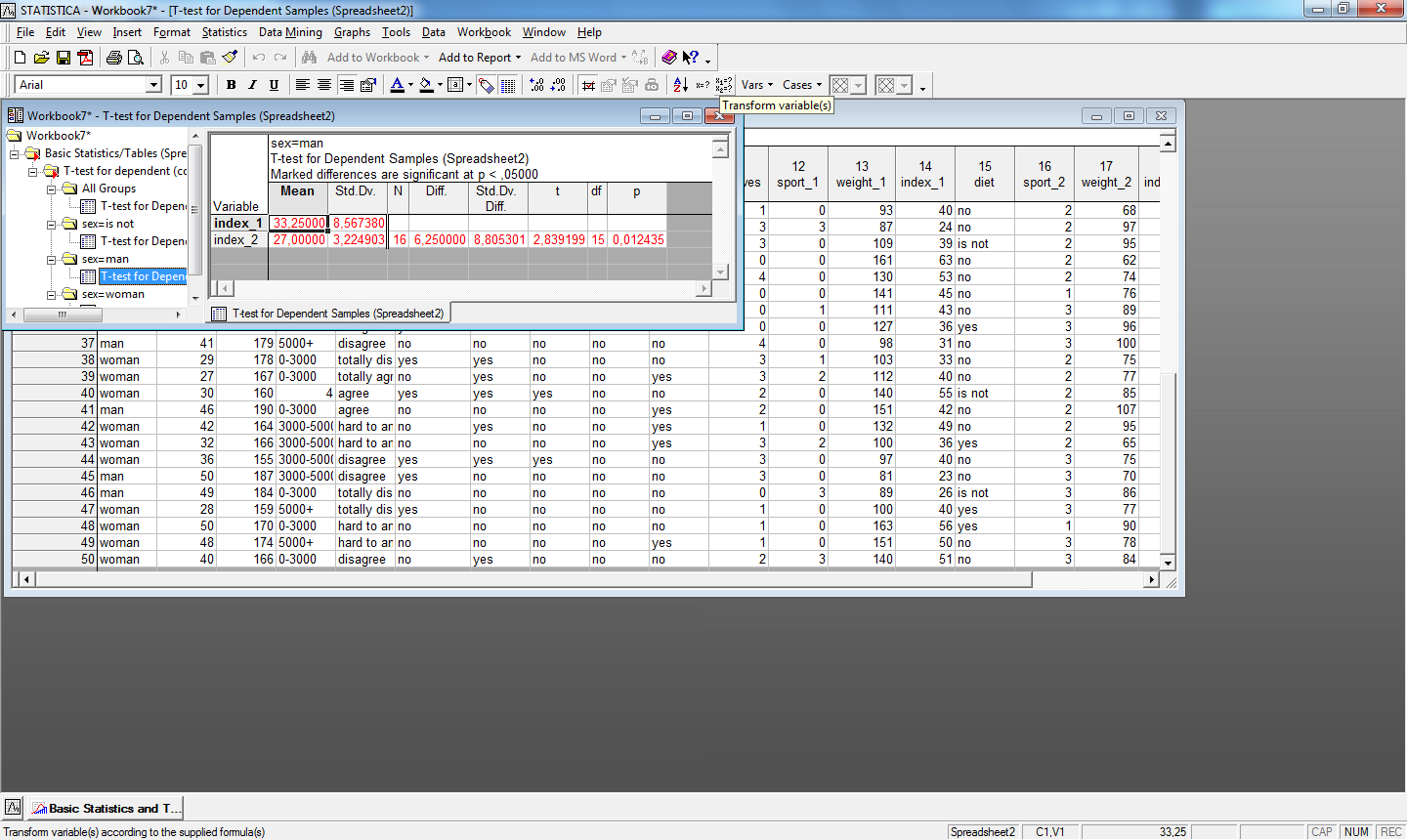
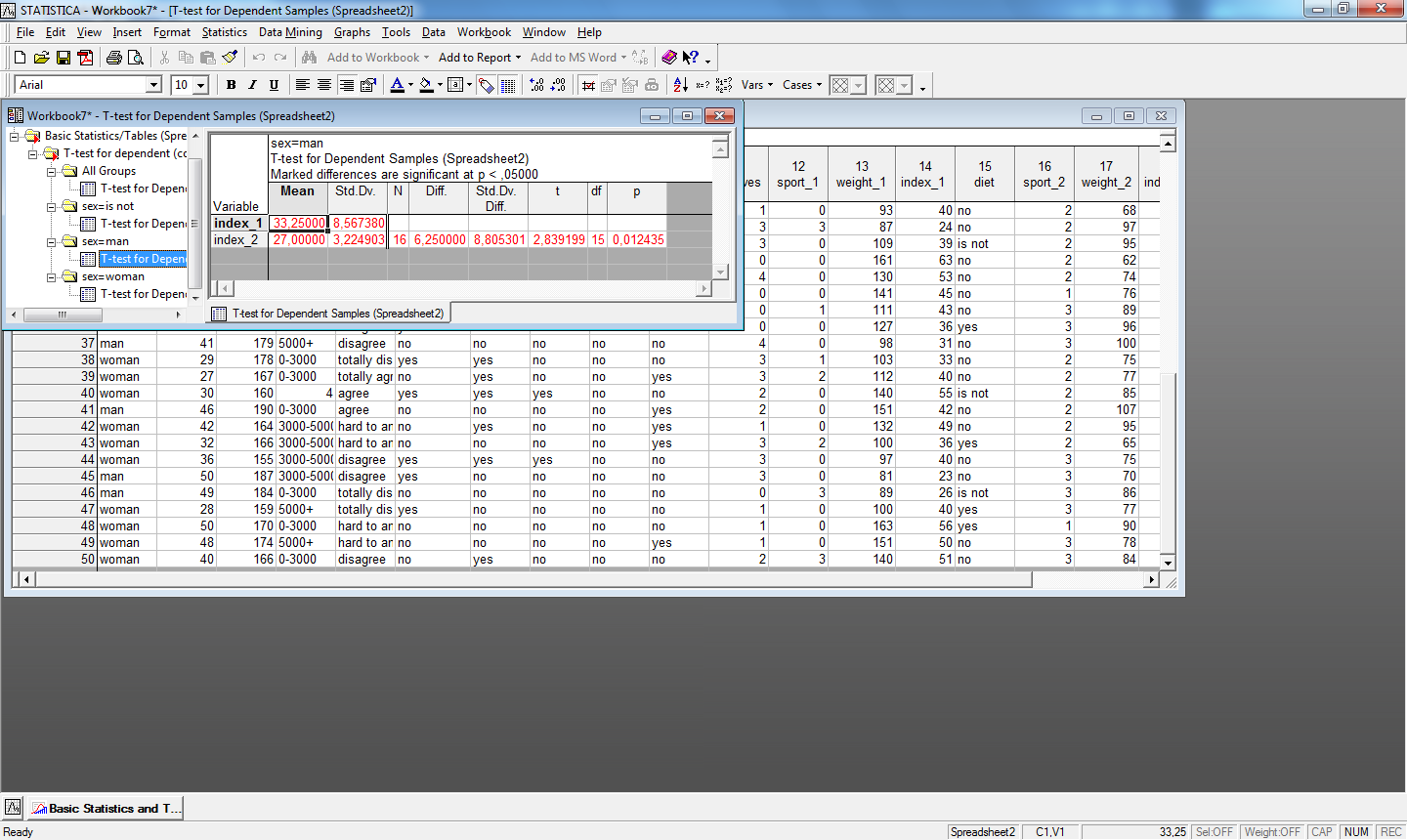
Рис.21. Применение t-критерия для зависимых выборок по группирующей переменной (сравнение средних двух переменных)

2.3. Применение t-критерия для одной выборки

t-критерий для одной выборки позволяет проверить гипотезу о равенстве выборочного среднего некоторому заданному числу.

Для того, чтобы сравнить среднее выбороки с конкретным заданным значением необходимо использовать следующую последовательность команд:

Statistics (Статистики) – Basic Statistics and Tables (Основные статистики и таблицы) - t-test, single sample (t- тест для одной выборки)

В открывшемся диалоговом окне (рис.22.) необходимо указать переменную для анализа и в поле Test all means against необходимо ввести значение для сравнения.

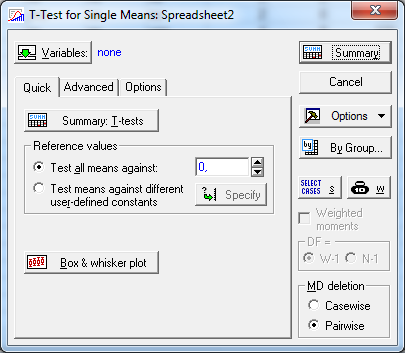
Рис.22. ДиалоговоеокноT-Test for Single Means

После нажатия на кнопку Summary на экран будет выведена таблица результатов t-критерия.

Пример сравнения среднего индекса массы тела до программы похудения по сравнению с критическим (30) представлен на рис.23.

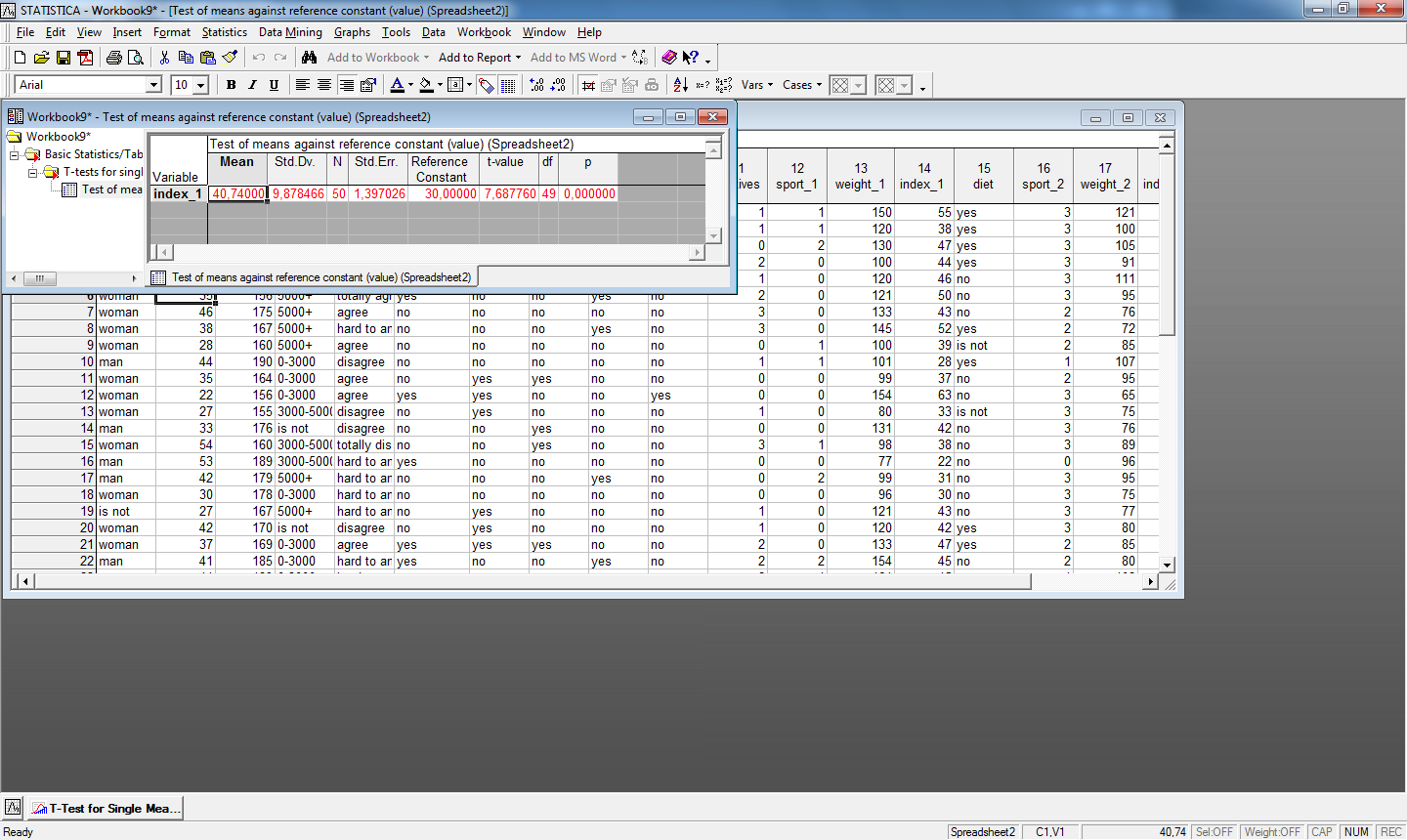
Рис.23. Применение t-критерия для одной выборки

Из таблиц видно, что среднее значение переменной index_1 составляет 40,7400 и статистически достоверно отличается от 30 ( p < 0,001).

Приложение 1

При интерпретации полученных результатов использовать следующие обозначения:

Std. Error	стандартная ошибка	Является мерой стабильности среднего значения. Вычисляется как отношение стандартного отклонения к квадратному корню объема выборки N
F	F-критерий	Величина, характеризующая соотношение дисперсий двух распределений
Sig	значимость (p-уровень значимости )	Величина указываю на то, что разницу двух дисперсий можно считать незначимой
t	t-критерий	Является мерой схожести/ различия Определяется как отношение разности средних значений к стандартному отклонению
df	число степеней свободы	вычисляется как разность объема выборки и числа групп. В данном случае число степеней свободы 100-2=98 для независимых выборок и 100-1=99 для зависимых и расчета t-критерия для одной выборки
Sig. (2-Tailed)	двухсторонняя значимость	означает вероятность того, что разность между средними значениями является случайной
Mean Difference	разность средних	разность между двумя средними значениями
Std. Deviation	стандартное отклонение	стандартное отклонение разности между средними значениями
Correlation	корреляция	мера связи двух переменных. В данном случае используется коэффициент корреляции Пирсона
95% Confidence Interval	95%-ый доверительный интервал	в данном случае понятие «доверительный интервал» относится к разности между средними значениями выборок.