2. Реализация в statistica

STATISTICA позволяет применять четыре варианта t-критерия:

• критерий для независимых выборок по группам (t-test, independent by groups),

• критерий для независимых переменных (t-test, independent by variables),

• критерий для зависимых выборок (t-test, dependent samples),

• критерий для одной выборки (t-test, single sample).

2.1. Применение t-критерия для независимых выборок

Данный метод сравнения позволяет проверить гипотезу о том, что средние значения двух генеральных совокупностей, из которых извлечены сравниваемые независимые выборки, отличаются друг от друга.

В программе STATISTICA реализовано два способа сравнения данных с помощью данного метода, которые основаны на обработке двух разных матриц данных: по группам (by groups), если в таблице с данными есть группирующая переменная и по переменным (by variables), если данные внесены в самостоятельные столбцы.

Для применения t-критерия для независимых выборок по группам необходимо использовать следующую последовательность команд:

Statistics (Статистики) – Basic Statistics and Tables (Основные статистики и таблицы) - t-test, independent by groups (t-критерий для независимых выборок по группам)

В результате чего откроется диалоговое окно (рис.12), в котором необходимо указать зависимую переменную (Dependent) и группирующую переменную (Grouping), градациям которой соответствуют независимые выборки для вычисления t-критерия. Группирующая переменная должна быть дискретной и иметь две градации.

Рис.12.ДиалоговоеокноT-Test for independent Samples by groups

После выбора группирующей перемен в поле Code for Group 1 и Code for Group 2 появятся градации группирующей переменной. Чтобы рассчитать значение теста Левана для проверки равенства дисперсии в двух группах, необходимо перейти на вкладку Options (Опции) и установить флажок Levene’s test. Также в STATISTICA доступен критерий Брауна – Форсайта (Brown&Forsythe test). После нажатия на кнопку Summary на экран будет выведена таблица результатов вычисления t-критерия:

• Mean - среднее значение в каждой группе;

• t-value - значениеt-критерия Стьюдента;

• df - число степеней свободы;

• P - вероятность справедливости гипотезы о том, что сравниваемые средние значения не различаются;

• Valid N - объем каждой выборки;

• Std. dev.- стандартное отклонение для каждой выборки;

• F-ratio, Variances- значение F-критерия Фишера, с помощью которого проверяется гипотеза о равенстве дисперсий в сравниваемых выборках;

• P, Variances- вероятность справедливости гипотезы о том, что дисперсии сравниваемых выборок не различаются.

Анализ данных с помощью t-критерия, сравнения средних и меры отклонения от среднего в группах можно производить с помощью диаграмм размаха. Эти графики позволяют визуально оценить степень зависимости между группирующей и зависимой переменными.

Для того, чтобы на экран была выведена коробчатая диаграмма необходимо, в диалоговом окне T-Test for independent Samples by groups (рис.12), щелкнуть на кнопке Box&whisker plot, после чего на экран будет выведен ящик с усами.

Пример сравнения среднего значения индекса массы тела до программы похудения для мужчин и женщин представлен соответствующая диаграмма размаха представлены на рис.13. и рис.14.

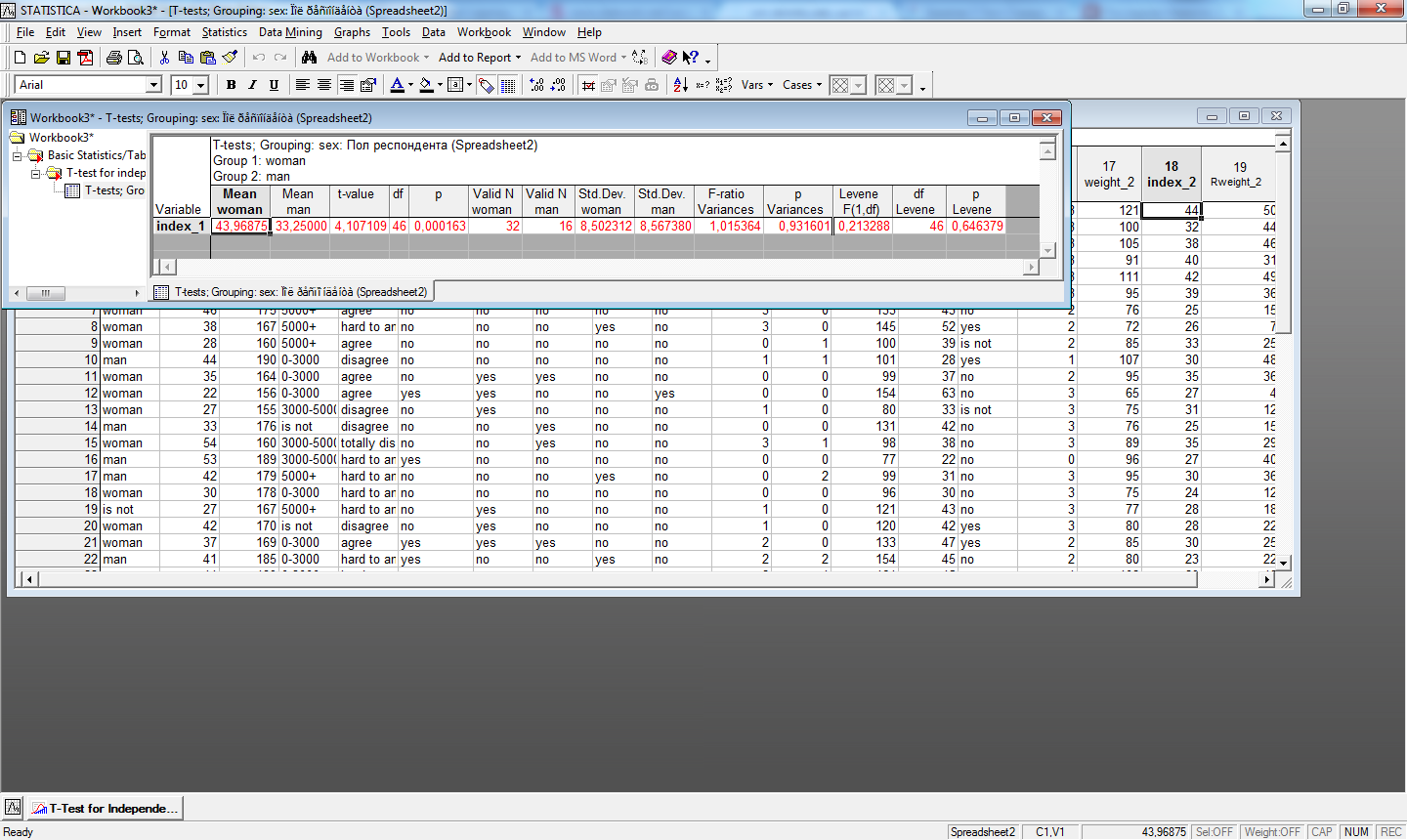
Рис.13. Применение t-критерия для независимых выборок

(по одной переменной)

Из результатов следует, что выборка из 32 женщин имеет средний индекс массы тела до программы похудения 43,9687, выборка из 16 мужчины — средний индекс массы тела до программы похудения 33,2500. Различия статистически достоверны на высоком уровне значимости (p = 0,000136). Критерий равенства дисперсий Ливиня указывает на то, что дисперсии двух распределений статистически значимо не различаются (p = 0,646), следовательно, применение t-критерия корректно.

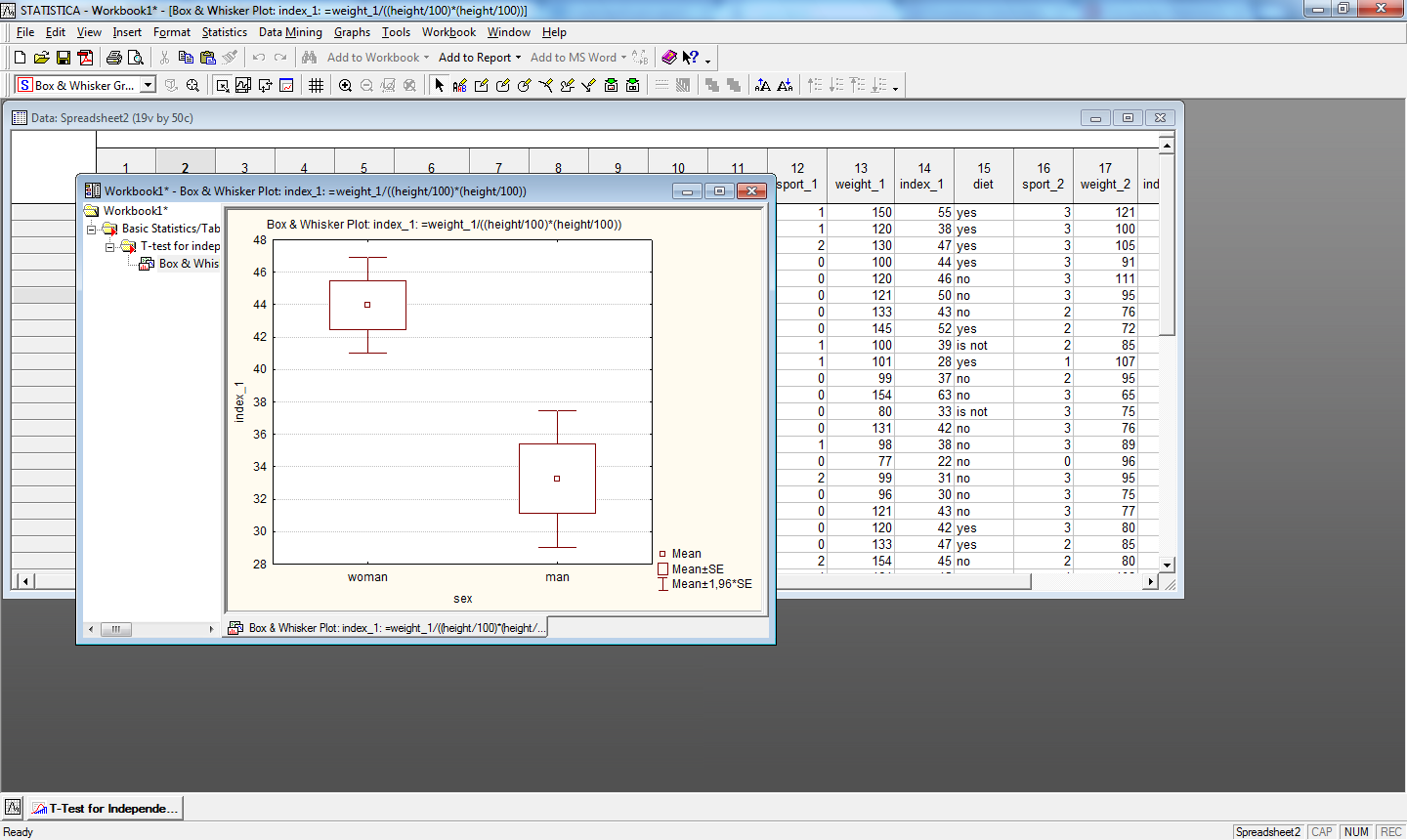
Рис.14. Коробчатая диаграмма для переменной index_1, сгруппированной по переменой sex

На рис.15. приведен пример сравнения индексов массы тела до и после программы похудения для мужчин и женщин, а на рис.16. коробчатые диаграммы отдельно для переменной index_1 и index_2 сгруппированные по переменной sex

Рис.15. Применение t-критерия для независимых выборок

(по двум переменным)

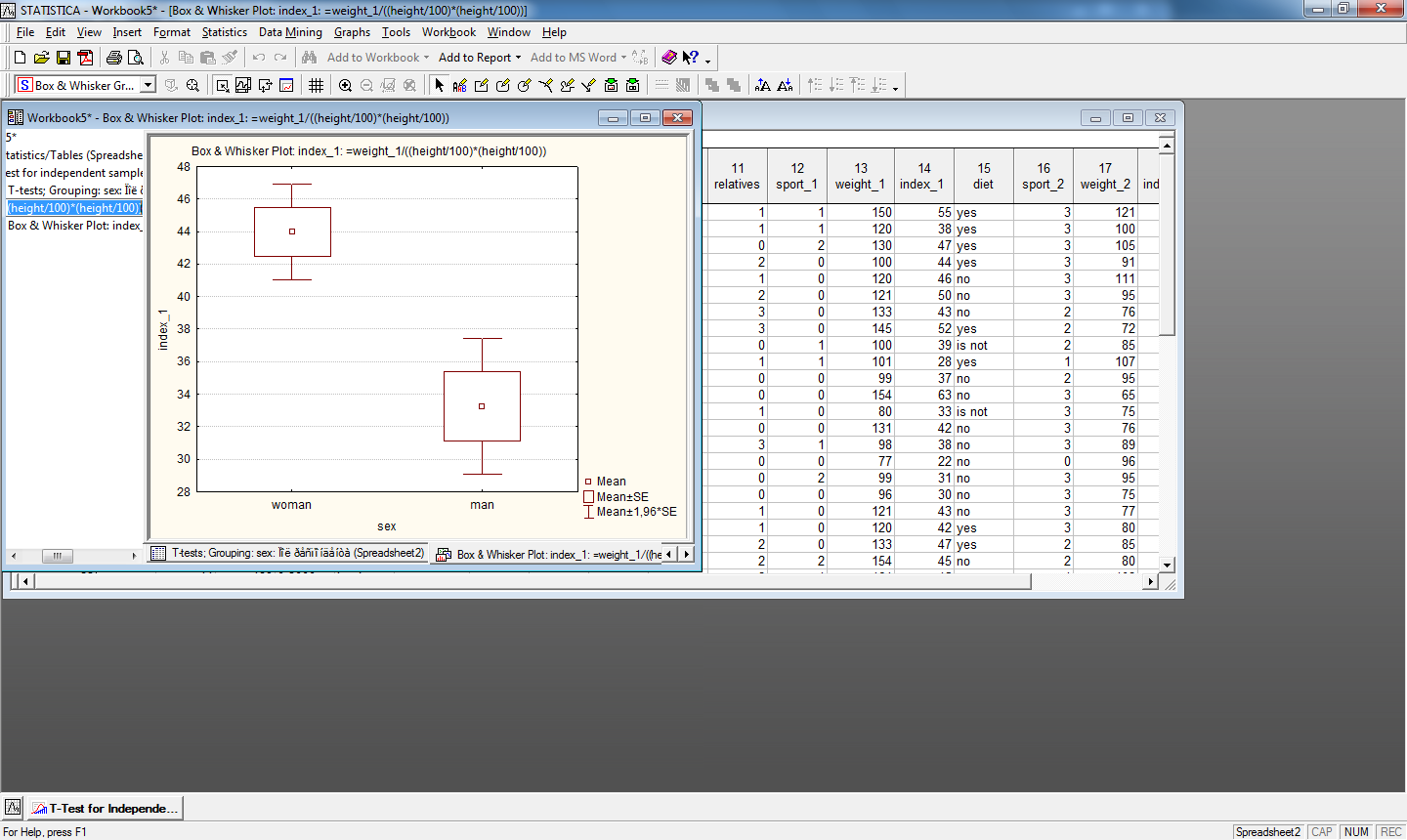
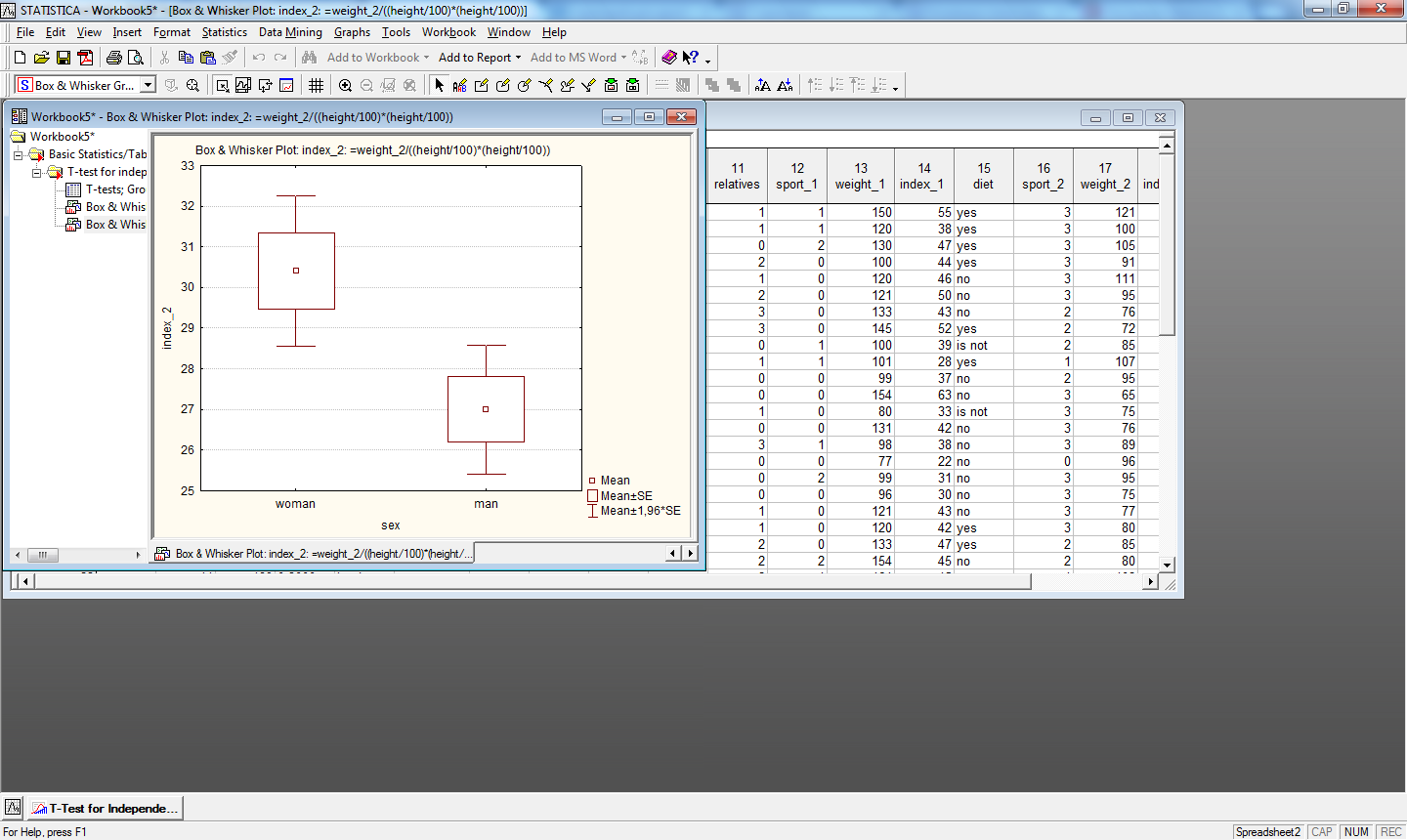
Рис.16. Коробчатые диаграммы для переменной index_1 и index_2 сгруппированные по переменной sex