1. Вибір та обгрунтування функціональної схеми пристрою

Структурна схема розробляється цифрового пристрою представлена ​​на рис.1.1

Рисунок 1.1. Структурна схема пристрою.

У наведеній структурній схемі цифрового пристрою з довільної комбінації вхідних інформаційних сигналів, комбінаційна схема (КС) формує відповідно до заданого алгоритму функціонування цифрового пристрою потенційні рівні сигналів, що відповідають значенням функцій І. Генератор тактових імпульсів (ГТІ) формує на виході імпульси, які підраховуються лічильником (СТ) і в задані такти, що формуються комбінаційними формувачами КС₁ і КС₂ пропускають сигнали на виходи А і В. На виході ЦП стоять логічні елементи (DD), які здійснюють логічне множення функцій КС і формувачів тактових імпульсів.

2. Синтез комбінаційної схеми пристрою

При синтезі комбінаційної схеми необхідно мінімізувати задані функції F₁ і F₂.

Основне завдання мінімізації - це вибір базису, який дозволяє отримати найпростішу реалізацію з мінімальною кількістю корпусів ІМС. Це необхідно для підвищення надійності цифрового пристрою, зменшення габаритів і собівартості.

При заданому числі змінних n = 4 наочним і зручним є графічне представлення логічних функцій у вигляді карт Карно, де логічна функція представляється сукупністю одиничних значень в тих клітинах карти, яким відповідають певні мінтерми.

Твір всіх логічних змінних з прямим або інверсним значеннями, для комбінації яких логічна функція істинна, дорівнюють одиниці.

Використовуючи цей метод, отримуємо функцію в мінімально діз'юнктівнії нормальній формі (МДНФ).

Задана логічна функція може бути представлена ​​і нульовими значеннями клітин на карті Карно, але при цьому логічна функція представляється у інверсному вигляді, тобто для того, щоб синтезувати схему, потрібно виконати наступні операції:

1. мінімізація логічних функцій І;

2. перетворення функцій для реалізації в заданому елементному базисі;

3. схемна реалізація функцій.

Мінімізація функції F₁ по "1" та її схемна реалізація в базисах І-НІ та І-АБО-НІ

На карту Карно (мал.2.1.1) наносимо одиничні значення функції та її байдужий набір.

; .

Малюнок 2.1.1. Карта Карно по "1".

Після проведення мінімізації за трьома контурам, отримаємо вираз для функції:

(2.1.1)

Для схемної реалізації функції по "1" в базисі І-НІ варто перетворити вираз (2.1.1), скориставшись законами інверсії. В результаті перетворення отримаємо:

; (2.1.2)

; (2.1.3)

Схемна реалізація функції по "1" наведена на мал. 2.1.2.

Малюнок 2.1.2. Схемна реалізація функції по "1" в базисі І-НІ.

При цій схемнії реалізації потрібно 3 корпуси ІМС:

DD1 - К155ЛН1;

DD2 - К155ЛА3;

DD3 - К155ЛА4.

Для схемної реалізації функції по "1" в базисі І-АБО-НІ потрібно взяти інверсне значення функції (2.1.1). При схемнії реалізації це буде враховано, тобто на виході поставимо інвертор.

. (2.1.4)

Схемна реалізація функції по "1" в базисі І-АБО-НЕ наведена на мал. 2.1.3.

Малюнок 2.1.3. Схемна реалізація функції по "1" в базисі І-АБО-НІ.

Тут необхідно використовувати 3 корпуси ІМС:

DD1 - К155ЛН1;

DD2 - K155ЛД1;

DD3 - К155ЛР3.

Мінімізація функції F1 по "0" і її схемна реалізація в базисах  І – НІ  і І-АБО-НІ

Мінімізацію функції з нульовим значенням зробимо також за допомогою карти Карно (рис. 2.2.1), на полі якої наносимо нульові значення функції та її байдужий набір.

Малюнок 2.2.1. Карта Карно для F₁по "0".

Мінімізацію проводимо по чотирьом контурам. Інверсне значення функції матиме вигляд:

(2.2.1)

Після перетворення за допомогою законів інверсії отримаємо значення функції з "0" у вигляді, відповідному її схемної реалізації в базисі І-АБО-НІ.

(2.2.2)

(2.2.3)

Зробимо схемну реалізацію функції з "0" в базисі І-НІ згідно з виразом (2.2.3) - (мал. 2.2.2) і в базисі І-АБО-НІ згідно з виразом (2.2.1) - (мал.2.2.3 ).

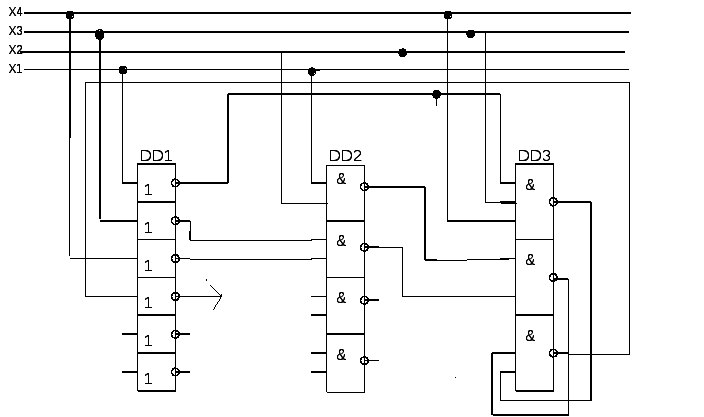
Малюнок 2.2.2. Схемна реалізація по "0" в базисі І-НІ.

За цієї схемної реалізації потрібно 3 корпуси ІМС:

DD1 - К155ЛН1;

DD2 - К155ЛА3;

DD3 - К155ЛА4.

Малюнок 2.2.3. Схемна реалізація функції по "0" в базисіІ-АБО-НІ.

За цієї схемної реалізації потрібно 3 корпусу ІМС:

DD1 - К155ЛН1;

DD2 - К155ЛД1;

DD3 - К155ЛР3.

Мінімізація функції F2 по "1" та її схемна реалізація в базисах І-НІ і І-АБО-НІ

Зробимо мінімізацію функції по "1" за допомогою карти Карно  (мал. 2.3.1).

; .

Малюнок 2.3.1. Карта Карно для по "1".

У результаті виконаної мінімізації за двома контурам отримаємо значення функції.

. (2.3.1)

За допомогою законів інверсії перетворимо значення функції.

; (2.3.2)

. (2.3.3)

Зробимо схемну реалізацію функції.

Малюнок 2.3.2. Схемна реалізація по "1" в базисі І-НЕ.

Тут:

DD1 - К155ЛН1;

DD2 - К155ЛА4.

Малюнок 2.3.3. Схемна реалізація по "1" в базисі І-АБО-НІ.

За цієї схемної реалізації буде потрібно два корпуси ІМС:

DD1 - К155ЛН1;

DD2 - К155ЛР3.

Мінімізація функції F2 по "0" і її схемна реалізація в базисах  І – НІ  і І-АБО-НЕ

Зробимо мінімізацію функції з нульовим значенням за допомогою карти Карно (рис. 2.4.1).

Малюнок 2.4.1. Карта Карно для по "0".

Зробимо мінімізацію за трьома контурам. Значення функції, мінімізованої за нульовими значенням, має вигляд:

. (2.4.1)

За допомогою законів інверсії перетворимо значення функції:

;

. (2.4.2)

Зробимо схемну реалізацію функції з "0".

Малюнок 2.4.2. Схемна реалізація по "0" в базисі І-НІ.

У цій схемі:

DD1 - К155ЛН1;

DD3 - K155ЛА4.

Малюнок 2.4.3. Схемна реалізація по "0" в базисі І-АБО-НЕ.

За цієї схемної реалізації буде потрібно два корпуси ІМС:

DD1 - К155ЛН1;

DD2 - K155ЛР4.

Вибір оптимальної структури комбінаційної схеми пристрою

Метою курсового проекту є створення цифрового пристрою з мінімальною кількістю корпусів ІМС.

При спільній схемнії реалізації функцій можна обійтися трьома корпусами ІМС, бажано проектувати цифровий пристрій на одній серії ІМС.

Ретельно проаналізувавши всі виконані схемні реалізації, вибираємо схемну реалізацію функції в базисі І-АБО-НІ, мінімізовану за нульовими значеннями і схемну реалізацію функції (також в базисі І-АБО-НІ), мінімізовану за нульовими значеннями.

Оптимальна комбінаційна схема наведена на мал. 2.5.1.

При цьому буде використано 4 корпуси ІМС:

DD1 - К155ЛН1;

DD2-К155ЛД1;

DD3 - К155ЛР3;

DD4 - К155ЛР3.

Причому вільні логічні елементи ІМС DD1 - К155ЛН1 можуть використовуватися при синтезі формувача тактових інтервалів.

Малюнок 2.5.1. Комбінаційна схема.

1.3. Синтез комбінаційної схеми цифрового пристрою

Головним етапом синтезу комбінаційної схеми є мінімізація заданих логічних функцій F1 і F2 з метою отримання найпростішого алгебраїчного виразу для кожної з них, тобто мінімальної діз'юнктівної нормальної форми (МДНФ) з подальшою реалізацією схемної мінімальним числом логічних елементів і, відповідно, мінімальною кількістю цифрових ІМС. У цьому курсовому проекті мінімізація кожної з функцій повинна бути виконана як за одиничним, так і нульовим значенням цих функцій.

При числі вхідних логічних змінних до (5  6) найбільш ефективним методом є мінімізація логічних функцій з використанням карт Карно (карт мінтермів).

Число клітин карти Карно дорівнює числу всіх можливих комбінацій  n логічних змінних, тобто N = 2n, а кожна клітина карти Карно відповідає певному минтерм (малюнок 2).

М алюнок 2 - Карта Карно для функції чотирьох змінних

На мал.2 в) рискою позначені ті рядки або стовбці карти Карно, в мінтерм яких відповідна логічна змінна входить в прямому вигляді. При виконанні процедури мінімізації необхідно пам'ятати визначення «суміжних» клітин карти Карно, під якими розуміють такі клітини карти, мінтерми яких відрізняються значенням тільки однієї логічної змінної (в одному минтермі вона має пряме значення х, в іншому - інверсне).

Застосування циклічного коду нумерації клітин карти Карно призводить до того, що «суміжними» є не тільки сусідні клітини карти, але і крайні клітини кожного рядка і кожного стовпця.

Мінімізацію логічних функцій з їх одиничним значенням рекомендується виконувати в такій послідовності:

У відповідні клітини карти Карно ставляться одиниці для мінтермів функції, зазначені в завданні. Для функції F1 аналогічним чином на карті Карно проставляються мінтерм байдужих наборів, які доцільно позначити «зірочкою» ().

Визначаються мінімізують контуру, що охоплюють клітини карти Карно з одиничними значеннями, при цьому в кожен контур має входити максимально можливе число 2К «суміжних» клітин, а число контурів повинно бути мінімальним, всі вони повинні бути незалежними, тобто відрізнятися значенням хоча б одного мінтерма. Байдужі набори логічних змінних включаються в контур мінімізації з присвоєнням йому одиничного (нульового) значення тільки в тому випадку, коли їх використання дозволяє спростити алгебраїчне вираз минимизируемой функції. Мінімізують контуру можуть перетинатися; бути як замкнутими, так і розімкнутими, охоплюючи крайні клітини рядків або стовпців, або кутові клітини карти Карно (мал. 3).

М алюнок 3 - Вибір контурів мінімізації на карті Карно

_____________ - За одиничними значенням функції;

_ _ _ _ _ _ _ _ _ - За нульових значень функції

З використанням закону склеювання логічних змінних виконується процедура зчитування імпліканти відповідного контуру, при цьому з твору логічних змінних виключаються ті змінні, які в даному контурі змінюють своє значення. При наявності в мінімізуючому контурі 2К «суміжних» клітин з імпліканти виключаються До логічних змінних.

Для функції (див. мал.3) МДНФ представлена ​​алгебраїчним виразом:

Оптимальний вибір мінімізують контурів забезпечує одержання алгебраїчного виразу для заданої функції у вигляді суми імплікант усіх контурів, при чому функція представляється в мінімальній ДНФ, тобто її подальше спрощення неможливо.

Мінімізація логічний функції може бути виконана за нульовим значенням цієї функції, при цьому отримують інверсне значення шуканої функції (див. мал. 3).

У цьому РГЗ повинна бути виконана роздільна мінімізація логічних функцій F1 і F2 за одиничними і нульовим значенням цих функцій з подальшою схемної реалізацією кожної МДНФ в заданому елементному базисі І-НІ, І-АБО-НІ.

Перед виконанням етапу схемної реалізації логічних функцій необхідно здійснити вибір серії інтегральних мікросхем, що задовольняють вимогам за швидкодієюю, споживанням потужності і мають найбільш широкий функціональний набір логічних елементів, наприклад, серію К155 (КР155) (Додаток В). При використанні логічних елементів інших серій необхідно звернути увагу на сумісність основних електричних і динамічних параметрів логічних елементів цих серій.

Важливо пам'ятати те, що в даному РГЗ схемної реалізації підлягають логічні функції, що представлені в прямому вигляді.

При схемнії реалізації логічних функцій в базисі І-НІ необхідно попереднє перетворення алгебраїчного виразу за допомогою законів інверсії (теорем  де Моргана) до такого виду, в якому використовується тільки кон'юнкція і інверсія, при цьому доцільно використовувати спеціалізовану мікросхему блоку інверторів (К155ЛН1) для отримання інверсних значень логічних змінних і їх функцій.

Наприклад, функція для схемної реалізації в зазначеному елементному базисі приводиться до вигляду

При схемної реалізації в базисі І-НІ вільні інформаційні входи логічних елементів з метою підвищення завадостійкості підключаються до джерела живлення через резистор опором 1 кОм.

При схемнії реалізації мінімізованих логічних функцій в базисі І-АБО-НІ необхідно хоча б один інформаційний вхід не використовуваного елемента І заземлити, інакше на його виході буде постійно рівень логічної одиниці, а в цілому елемент І-АБО-НІ - в нульовому стані незалежно від інформаційних сигналів на інших входах.

Необхідно звернути увагу на те, що цифрові мікросхеми І-АБО-НІ часто мають додатковий вхід розширення по АБО (входи А, В мікросхем К155ЛР1, К155ЛР3, К155ЛР4) для підключення входів мікросхем К155ЛД1, К155ЛД3, що істотно розширює функціональні можливості цих мікросхем, при цьому не використовуються входи розширення по АБО мікросхем І-АБО-НІ залишаються вільними на відміну від входів елементів І.

Після мінімізації логічних функцій F1 і F2 за одиничними і нульовим значенням цих функцій, схемної реалізації їх в елементних базисах І-НІ, І-АБО-НІ на останньому етапі синтезу комбінаційної схеми цифрового пристрою на підставі восьми структур необхідно створити узагальнену оптимальну структуру комбінаційної схеми, реалізовує одночасно логічні функції F1 і F2 і виконану з максимальним використанням функціональних можливостей цифрових мікросхем і при мінімальному числі корпусів ІМС.

В якості вихідних логічних пристроїв, що виконують логічну операцію А = F1.T1 (або В = F2.T2) можуть бути застосовані двовхідні елементи 2 І мікросхеми К155ЛІ1, при цьому вихідні рівні сигналів А і В будуть відповідати значенням логічних функцій F1 і F2 тільки при одиничних значеннях відповідно Т1 і Т2.

У даному РГЗ у додатки включаються такі документи:

- Таблиця істинності цифрового пристрою з тимчасовим поділом сигналів;

- Тимчасові діаграми роботи цифрового пристрою.

СПИСОК ДЖЕРЕЛ ІНФОРМАЦІЇ

1. Алексенко О.Г. Мікросхемотехніка. - М.: Вища школа, 1991.

2. Горбачов Г.Н., Чаплигін Е.Е. Промислова електроніка. - М.: Вища школа, 1988.

3. Гусєв В.Г., Гусєв Ю.М. Електроніка. - М.: Вища школа, 1991.

4. Забродін Ю.С. Промислова електроніка. - М.: Вища школа, 1982.

5. Із'юрова Г.І., Корольов Г.В., Терехов В.А. та ін Розрахунок електронних схем. - М.: Вища школа, 1988.

6. Інтегральні мікросхеми: Довідник. / Под ред. Тарабрина В.В. / - М.: Вища школа, 1985.

ДОДАТКИ

Базові логічні елементи серії К155

Г