
сигналы4
.docxСанкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) (СПбГЭТУ)
Кафедра ВТ
РЕФЕРАТ
по дисциплине: «Цифровая обработка сигналов»
на тему: «Линейная свертка детерминированных последовательностей»
Выполнил:
Проверил:
г. Санкт-Петербург, 2014 г.
Оглавление
1. Введение 3
2. Линейная свертка 4
3. Циклическая свертка 5
4. Секционированные свертки 7
5. Литература 11
Введение
Операция свертки:
s(t)
= x(t) * h(t) =
 (1)
(1)
Свертка позволяет рассчитать сигнал s(t) на выходе линейного фильтра с импульсной характеристикой h(t), при входном сигнале x(t).
В дискретном случае различают два вида сверток: линейную (или апериодическую) и циклическую. Циклическую свертку еще часто называют круговой или периодической.
Линейная свертка
Рассмотрим линейную свертку. Пусть имеется два дискретных сигнала a(n), n=0..N-1, и b(n), n=0..M-1. В общем случае длины этих сигналов N и M могут отличаться. Линейной сверткой сигналов a(n) и b(n) называется дискретный сигнал вида:
s(n)
= a*b =
 (2)
(2)
Для вычисления линейной свертки сигналы a(n) и b(n) сдвигают относительно друг друга почленно перемножают и складывают. При этом предполагается, что a(n) = 0 при n<0 и n>N, а также b(n)=0 при n<0 и n>M
Графическое представление линейной свертки представлено на рисунке 1.
 Рисунок
1: Графическое представление линейной
свертки
Рисунок
1: Графическое представление линейной
свертки
Отсчеты сигнала b(n) сдвигаются относительно отсчетов последовательности a(n) все возможные перекрывающиеся отсчеты почленно перемножаются и складываются.
На рисунке 2 приведен пример вычисления линейной свертки двух сигналов a(n) = [2,1,3,-1] длиной 4 отсчета и b(n)=[-1,1,2] длиной 3 отсчета.
 Рисунок
2: Пример вычисления линейной свертки.
Рисунок
2: Пример вычисления линейной свертки.
Необходимо отметить, что сигнал b(n) при вычислении свертки отражается слева-направо, поскольку b(0)=-1 самый первый отсчет (самый ранний по времени) и обрабатываться он также должен первым.
Циклическая свертка
Рассмотрим теперь циклическую свертку. В случае циклической свертки предполагается, что дискретные сигналы a(n) и b(n) - периодические с одинаковым периодом N отсчетов. Тогда круговой сверткой сигналов a(n) и b(n) называется сигнал вида:
s(n)
=
 (3)
(3)
Результат циклической свертки также имеет длину N отсчетов.
Рассмотрим циклическую свертку на примере двух сигналов a(n)=[2,1,3,-1] и b(n)=[-1,3,2,1] . Графически вычисление циклической свертки представлено на рисунке 3.
 Рисунок
3: Вычисление циклической свертки
Рисунок
3: Вычисление циклической свертки
Красной линией отмечены границы периодов повторения сигнала b(n-m). Заметим, что в силу периодичности сигналов b(-m)=b(N-m).
Вычислим свертку пошагово:
s(0)
=
Теперь рассчитаем s(1):
s(1)
=
 (5)
(5)
Аналогично можно рассчитать s(2) = 3 и s(3)=14.
Используя циклическую свертку можно рассчитать линейную свертку двух сигналов. Для этого необходимо каждый из сигналов a(n) и b(n) длительностью M и N отсчетов соответственно дополнить нулями до длины M+N-1.
Приведем пример вычисления линейной свертки через циклическую для a(n)=[2,1,3,-1] длиной 4 отсчета и b(n)=[-1,1,2] длиной 3 отсчета (этот пример был рассмотрен выше).
Дополним нулями a(n)=[2,1,3,-1,0,0] и b(n)=[-1,1,2,0,0,0], так чтобы в каждой последовательности было по 6 отсчетов.
Вычислим циклическую свертку как это показано на рисунке 4.
 Рисунок
4: Вычисление линейной свертки через
циклическую <
Рисунок
4: Вычисление линейной свертки через
циклическую <
Можно сравнить с результатом самого первого примера для линейной свертки и убедится в том, что значения совпадают.
Секционированные свертки
Секционная свёртка используется, когда количество элементов одной из последовательностей в несколько раз больше, чем количество элементов другой. Секционная свёртка может выполняться двумя методами вычисления. Они основаны на разбиении более длинной последовательности на секции и вычислении частичных сверток, из которых затем формируется искомая выходная последовательность.
Первый
из них называется методом перекрытия
с суммированием. Сущность этого метода
иллюстрируется на рис.5. Для простоты
положим, что последовательность x(n) не
ограничена, a h(n) содержит
 отсчетов.
Разделим последовательность x(n) на
смежные секции длиной по
отсчетов.
Разделим последовательность x(n) на
смежные секции длиной по  отсчетов
(рис. 5). Выбор
отсчетов
(рис. 5). Выбор 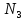 довольно
сложен, но хорошие результаты получаются,
если
довольно
сложен, но хорошие результаты получаются,
если
 является
величиной того же порядка, что и
является
величиной того же порядка, что и
 .Итак,
входная последовательность x(n) представляется
в виде
.Итак,
входная последовательность x(n) представляется
в виде
x(n)
=

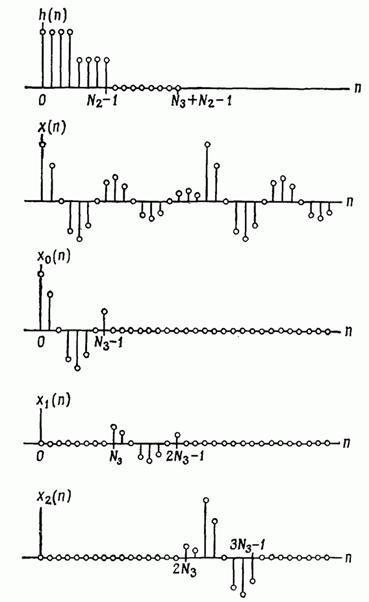
рис.5. - Метод перекрытия с суммированием.
Где

Линейная свертка последовательностей x(n) и h(n) равна
y(n)=

рис.6. - Формирование выходных значений свертки при использовании метода перекрытия с суммированием.
Длина
каждой из частичных сверток в сумме (4)
равна ( ) отсчетам,
т. е. имеется участок длиной в (
) отсчетам,
т. е. имеется участок длиной в (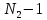 ) отсчетов,
на котором k-я
и (k+1)-я
частичные свертки перекрываются, поэтому
их отсчеты на участке перекрытия нужно
сложить. На рис. 6 показано, как расположены
и как суммируются соседние частичные
свертки
) отсчетов,
на котором k-я
и (k+1)-я
частичные свертки перекрываются, поэтому
их отсчеты на участке перекрытия нужно
сложить. На рис. 6 показано, как расположены
и как суммируются соседние частичные
свертки
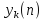 .
Рассмотренный метод был назван методом
перекрытия с суммированием именно
потому, что промежуточные частичные
свертки перекрываются и для получения
конечного результата их необходимо
сложить.
.
Рассмотренный метод был назван методом
перекрытия с суммированием именно
потому, что промежуточные частичные
свертки перекрываются и для получения
конечного результата их необходимо
сложить.

рис.7 -. Метод перекрытия с накоплением.
Другой
метод вычисления линейной свертки
последовательностей, одна из которых
значительно длиннее другой, также
основан на секционировании более длинной
последовательности. Его называют методом
перекрытия с накоплением, причем в
данном случае перекрываются входные,
а не выходные секции. Ошибочные отсчеты
круговых сверток отдельных секций
отбрасываются. Остальные отсчеты
накапливаются и из них формируется
конечный результат. Рассмотрим конкретный
пример (рис. 7). Последовательность
h(n) содержит
 отсчетов,
а последовательность x(n) разделена
на секции
отсчетов,
а последовательность x(n) разделена
на секции
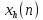 длиной
по (
длиной
по (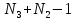 )
отсчетов, перекрывающиеся
друг с другом на участках длиной
по
)
отсчетов, перекрывающиеся
друг с другом на участках длиной
по  отсчетов.
(Отметим, что участок перекрытия находится
в конце последовательности
отсчетов.
(Отметим, что участок перекрытия находится
в конце последовательности  .
Это удобно для вычисления круговой
свертки с помощью ДПФ.)
.
Это удобно для вычисления круговой
свертки с помощью ДПФ.)
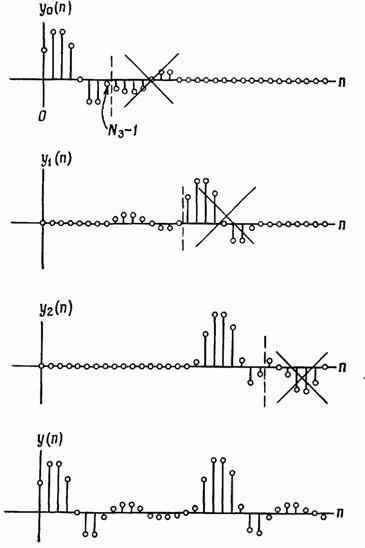
рис. 8. - Формирование выходных значений свертки при использовании метода перекрытия с накоплением.
Для
каждой секции вычисляется круговая
свертка последовательностей h(n) и 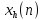 ,
содержащая (
,
содержащая ( )
отсчет. В результате
получается набор последовательностей
)
отсчет. В результате
получается набор последовательностей
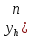 ),
изображенных па рис.8. Последние
(
),
изображенных па рис.8. Последние
( ) отсчетов
каждой из последовательностей
) отсчетов
каждой из последовательностей
 отбрасываются
(они неверны из-за циклического характера
свертки), а остальные присоединяются к
правильным отсчетам последовательности
отбрасываются
(они неверны из-за циклического характера
свертки), а остальные присоединяются к
правильным отсчетам последовательности
 и
т. д. В результате получается искомая
последовательность, тождественная
свертке y(n).
Итак, используя метод перекрытия с
суммированием или метод перекрытия с
накоплением, можно сравнительно легко
найти свертку короткой и очень длинной
последовательностей, причем результат
получается в виде отдельных небольших
секций, которые объединяются соответствующим
образом в одну последовательность.
и
т. д. В результате получается искомая
последовательность, тождественная
свертке y(n).
Итак, используя метод перекрытия с
суммированием или метод перекрытия с
накоплением, можно сравнительно легко
найти свертку короткой и очень длинной
последовательностей, причем результат
получается в виде отдельных небольших
секций, которые объединяются соответствующим
образом в одну последовательность.
Литература
1. Цифровая обработка сигналов изображений : учеб. пособие / С.М. Ибатуллин ; Санкт-Петербургский государственный электротехнический университет им. В.И. Ульянова (Ленина) "ЛЭТИ" . - СПб. : Изд-во СПбГЭТУ "ЛЭТИ", 2006.
2. Цифровая обработка сигналов: учеб. пособие для вузов / А.Б.Сергиенко ; - СПб. : Питер, 2002.
3. Алгоритмы и процессоры цифровой обработки сигналов : Учеб. пособие для вузов / А. И. Солонина, Д. А. Улахович, Л. А. Яковлев. - СПб. : БХВ-Петербург, 2001.
4. Цифровая обработка сигналов = Understanding digital signal processing / Р. Лайонс ; пер. с англ. под ред. А. А. Бритова. - 2-е изд. - М. : Бином, 2007.
