Дискретное преобразование Фурье

Дискретное преобразование Фурье — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.

Пара непрерывного преобразования Фурье имеет вид:

Выражение для прямого преобразования имеет вид:

, k=0…N-1

для обратного:

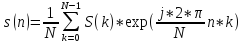, n=0…N-1

Выражение для ДПФ ставит в соответствие N отсчетам сигнала s(n), n=0…N-1, в общем случае комплексного, N отсчетов спектра S(k), k=0…N-1.

В непрерывном так и в дискретном случае, в выражении для обратного преобразования имеется нормировочный коэффициент. В случае интеграла Фурье это  , в случае обратного преобразования это . Можно отметить, что в случае непрерывного преобразования нормировочный коэффициент призван корректно отображать масштабирование сигнала во времени в частотную область и наоборот.

Другими словами, если последовательно рассчитать спектр некоторого сигнала, а после взять обратное преобразование Фурье, то результат обратного преобразования должен полностью совпадать с исходным сигналом. Нормировочный коэффициент уменьшает амплитуду сигнала на выходе обратного преобразования для того чтобы она совпадала с амплитудой исходного сигнала.

Быстрое преобразование Фурье

Прямое вычисление ДПФ для больших N (например, при обработке речевых сигналов длина одного фрагмента N достигает значения ) крайне неэффективно и может стать препятствием для обеспечения реального времени. Для вычисления N-точечного преобразования требуется произвести комплексных умножений и N(N-1) комплексных сложений, т.е. объем вычислений имеет порядок операций сложения и умножения комплексных чисел.

Для уменьшения вычислительных затрат разработаны алгоритмы быстрого вычисления ДПФ, называемые быстрым преобразованием Фурье (БПФ). Эти алгоритмы основаны на периодичности ядра преобразования . Идея БПФ состоит в том, чтобы разделить N-точечную последовательность, и продолжать такое деление каждой новой последовательности до тех пор, пока не останутся последовательности, состоящие только из двух элементов. Конечно, такое деление возможно лишь при N = .

Алгоритм БПФ с прореживанием по времени.

Исходная N-точечная последовательность x(n) делится на две N/2-точечных последовательности, одна из которых содержит отсчеты с нечетными номерами, а другая – с четными номерами:

четная последовательность

нечетная последовательность

при n = 0, 1, …, (N/2) – 1. Тогда N-точечное ДПФ исходной последовательности x(n) преобразуется в два N/2-точечных ДПФ:

X (k) =

где верхняя строка дает первые N/2 составляющих ДПФ X(k), а нижняя строка вторые N/2 составляющих, 0 ≤ k ≤ N/2 – 1. Далее аналогичным образом N/2-точечные ДПФ заменяются двумя N/4-точечными каждое, и т.д. Такая сортировка осуществляется до тех пор, пока не образуется N/2 последовательностей по два элемента в каждом. В результате N-точечное ДПФ сводится к m = этапами, на каждом их которых требуется вычислить N коэффициентов. Выражения показывают, что на каждом этапе требуется N комплексных сложений и N/2 комплексных умножений. Легко видеть из направленного графа, напоминающего крылья бабочки, чем и объясняется название «бабочка» самой операции и графа, на котором стрелкой обозначено умножение на .

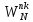Рис. – Операция «бабочка» с прореживанием по времени

Использование базовой операции «бабочка» снижает количество требуемых для вычисления N-точечного ДПФ комплексных сложений с до , что является существенной экономией вычислительных, а потому и временных ресурсов.

В результате сортировки отсчетов x(n) по нечетным и четным номерам входные данные записываются в необычном порядке, который называется двоичной инверсией, или бит-версией: например, если трехразрядное двоичное представление номера n отсчета x(n) имеет вид n = {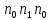}, то отсчет x{}, должен располагаться на месте x{. Это означает, что для правильного выполнения БПФ необходимо в исходном двоичном номере заменить порядок расположения разрядов на обратный (инверсный). Например, входной отчет x(6) =x(110) должен разместиться на 011 ->3 третьем месте, а третий отсчет x(3) окажется на шестом месте. При двоичной инверсии входной последовательности составляющие X(k) ДПФ будут расположены в естественном порядке.

Алгоритм БПФ с прореживанием по частоте

В этом случае входная последовательность x(n) делится пополам на N/2 первых и N/2 последних отсчетов и так до тех пор, пока не сформируются N/2 двухэлементных последовательностей. Базовая операция «бабочка» будет описываться следующим выражением, а ее направленный граф примет вид, показанный на рисунке.

X(k) =

Рис.-операция «бабочка» с прореживанием по частоте

Вычисление согласно данному алгоритму приводит к тому, что составляющие X(k) ДПФ располагаются в порядке, соответствующем бит реверсии, поэтому их необходимо пересортировать согласно естественному порядку. Например, X(3) = X(011) следует разместить на шестом месте, т.к. инверсный номер оказывается равным 110 ->6.

Двумерное дискретное преобразование Фурье

Двумерный дискретный сигнал (его также называют последовательностью или массивом) - это функция, определенная на совокупности упорядоченных пар целых чисел. Так,

x = {x (), -∞ <

Отдельные элементы последовательности будем называть отсчетами. Тогда x() представляет собой отсчет последовательности x в точке (). Значения отсчетов могут быть вещественными или комплексными. Если и 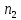считать переменными величинами, выражение x() можно рассматривать как обозначение всей последовательности. Хотя такое обозначение некорректно, оно широко используется в технической литературе и не должно приводить к недоразумениям.

Иногда может оказаться полезным рассматривать сигнал x не просто как функцию, определенную на множестве целочисленных значений ее аргументов, а как совокупность его отсчетов. При такой интерпретации не возникает соблазна определить x для каких-то значений и , не являющихся целыми числами.

Рис – графическое изображение двумерной последовательности

В соответствии с приведенным выше определением двумерные последовательности имеют бесконечную протяженность, поскольку и могут принимать любые целочисленные значения. Однако на практике для большинства двумерных последовательностей значения отсчетов известны только в конечной области плоскости ().

Обозначим через

x() = , ,

двумерное поле (двумерный сигнал), описывающее дискретное изображение размера 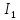строк и столбцов. Вне указанных границ этот сигнал не определен. Выполним периодическое продолжение данного финитного сигнала, введя двумерный периодический сигнал

Если сигнал существует только внутри прямоугольника со сторонами элементов, то сигнал определен на всей плоскостии является на ней прямоугольно-периодическим.

а)	б)
Рис. -. Реальное (а) и периодически продолженное (б) изображения

Любой периодический сигнал может быть представлен в виде ряда Фурье, но, в отличие от одномерных сигналов, двумерные описываются двумерным рядом Фурье, имеющим вид:

(1)

Базисные функции этого двумерного представления - двумерные комплексные экспоненты (иногда называемые комплексными синусоидами)

,

, (3)

имеющие, как и сигнал 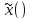 , прямоугольную периодичность с тем же периодом . Здесь  () - двумерный номер базисной функции, а величины  имеют смысл пространственных частот. Иногда пространственными частотами называют целочисленные величины  и .

Коэффициенты Фурье ряда  (1) образуют двумерный частотный спектр сигнала   и определяются формулой прямого преобразования Фурье:

(2)

Выражение (1), восстанавливающее сигнал  по его спектру , является обратным преобразованием Фурье. В справедливости преобразований  (1) и (2), называемых двумерным ДПФ, можно убедиться, подставив (2) в (1) и приведя правую часть полученного равенства к значению левой, т.е. к .

Заметим, что для точного представления дискретного сигнала  с двумерным периодом   элементов согласно формулам БПФ достаточно конечного  числа базисных функций (3) - ряд (1) является конечным. Это и понятно, поскольку сам представляемый сигнал содержит в одном периоде конечное число точек, т.е. имеет конечное число степеней свободы. Ясно, что число степеней свободы в спектре не может отличаться от числа степеней свободы в самом сигнале.

Остановимся на наиболее существенных свойствах двумерного дискретного спектра Фурье. Вычислим спектральные коэффициенты (2) в частотных точках ,  :

(4)

Поскольку при любых целых значениях 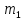 и   последний множитель в полученном выражении равен единице, то отсюда имеем равенство:

,

означающее прямоугольную периодичность двумерного ДПФ. Следовательно, картина двумерного ДПФ подобна картине двумерного периодически продолженного сигнала. Однако необходимо иметь в виду, что спектральные коэффициенты  являются комплексными числами, в том числе и при вещественном сигнале . Тогда возникает вопрос. Общее количество спектральных компонент, как установлено, равно . Комплексное число эквивалентно паре вещественных чисел - действительной и мнимой частям при алгебраическом или модулю и фазе при экспоненциальном представлении. Следовательно, полный спектр описывается   вещественными числами, что вдвое превышает размерность самого сигнала  . В этом, на первый взгляд, содержится противоречие. Оно находит свое разъяснение при дальнейшем изучении свойств двумерного ДПФ.

Преобразуем соотношение (4) следующим образом. Вместо частот   подставим частоты  .Выполним комплексное сопряжение обеих частей, что не нарушит равенства. В результате нетрудно получить выражение:

,

которым устанавливается однозначная связь между спектральными коэффициентами в двух различных точках спектрального прямоугольника  . Полученным соотношением и снимается противоречие, поскольку количество независимых спектральных коэффициентов уменьшается благодаря данной спектральной симметрии в два раза. Согласно установленному свойству, спектрально-сопряженной зависимостью связаны между собой спектральные коэффициенты, принадлежащие левому верхнему и правому нижнему углам прямоугольника  . Аналогично также связаны между собой коэффициенты Фурье из правого верхнего и левого нижнего участков спектрального прямоугольника .